INTRODUCTION
Geometric constructions are made with the aid a ruler or straightedge and compasses only. Drawings are made with the aid of additional instruments, such as protactor and ruler.
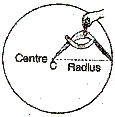
Construction of a Circle when its Radius is Known
Suppose you are asked to draw a circle of radius 3 cm. do as follows :
STEP 1.
Mark a point C with your pencil. This point will be the centre of the circle.
STEP 2.
Open the compass for the required radius, i.e., 3 cm, by putting the steel point on C and opening the pencil upto 3 cm.
STEP 3.
Hold the paper with one hand and swing the pencil leg of the compass around to draw a circle.
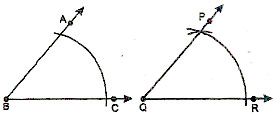
Construction of a Line Segment of a Given Length :
Suppose you have to draw a line segment 5.3 cm long.
Method 1. using ruler only
1. Mark any point in your exercise book and label it as A.
2. Place the ruler in such a way that the zero mark on the ruler coincides with A.
3. Now count 5 complete centimetres and 3 small divisions after the 5 cm mark and mark a point corresponding to this division on the exercise book.
4. Join A to this point as shown.
5. Label the second point as B.
Then AB is the required segment of length 5.3 cm.
Method 2. Using ruler and compass
STEP 1.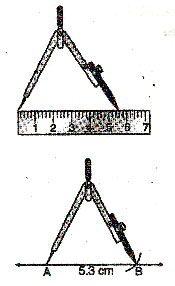
Draw any line segment which is longer than 5.3 cm.
STEP 2.
Mark a point on this line near one end as shown. Label it A.
STEP 3.
Use your compass to measure 5.3 cm on your ruler.
STEP 4.
Put the point of the compass on the line segment at A and draw an arc to cut the line as shown.
Then AB = 5.3 cm.
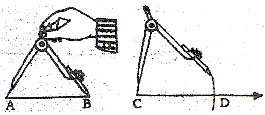
To construct a line segment congruent to a given line segment AB
STEP 1.
Draw a ray through any end point C. Open your compass so that the metal tip is on A and the pencil point is on B.
STEP 2.
Keep the compass opening same. Put the metal tip on the end point C of the ray and mark off a line CD congruent to AB.
Perpendicular Lines
Perpendicular lines are lines that intersect at right angles. The symbol ^ means "is perpendicular to".
Drawing Perpendicular Using Ruler and a Set- Square
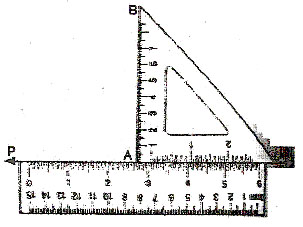
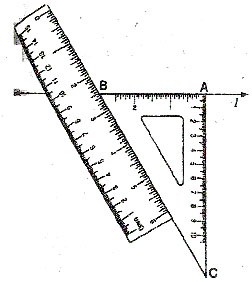
CASE 1 : To constant a line perpendicular to a given line l at a point P lying on it.
STEP 1.
Place a ruler on the paper with one of its long edges lying along the line l.
STEP 2.
Holding the ruler fixed, place a set-square ABC with the arm AC of its right angle A in contact with the ruler.
STEP 3.
Slides the set-square along the edge of the ruler until A conincides with P.
STEP 4.
Holding the set-square fixed in this position, draw with a sharp pencil a line PQ along the edge AB.
Then PQ is the required line perpendicular to the line l.
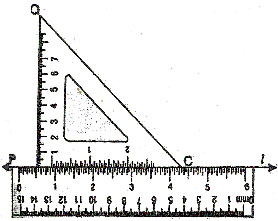
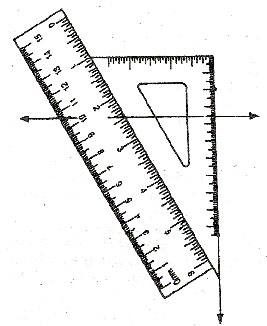
CASE 2 : To construct a line perpendicular to a given line l and passing through a given point P lying outside the given line.
SETP 1.
Place either of the set-squares so that one edge AB of the right angle A lies along l.
STEP 2.
Now hold the set-square fixed and place a ruler along the edge opposite to the right angle of the set-square.
STEP 3.
Holding the ruler firmly, silde the set-square along the ruler until the edge AC passes through the given point P.
STEP 4.
Draw line PQ along the edge AC of the set-square.
Then PQ is the required line perpendicular to the given line. l, through the point P not lying on it.
To Draw a perpendicular to a Given Line with a Rular, and compass :
CASE 1. At a point on the line.
Let AB be a given line and P be the point on it.
SETP 1.
With P as centre and any suitable radius draw an arc to cut the line AB at points M and N.
SETP 2.
With M and N as centres and radius of more than half MN, draw two arcs to cut at Q.
SETP 3.
Join PQ.
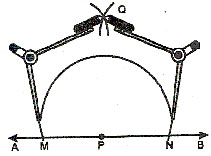
Then ray PQ is the perpendicular to the line AB at P.
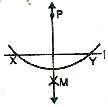
CASE 1. From a point outside the line.
STEP 1.
With P as centre and a suitable radius, draw an arc to cut the line l at X and Y.
STEP 2.
With X and Y as centres and a radius of more than half XY, draw two arcs to cut at M.
STEP 3.
Join PM. Then PM PERPENDICULAR l.
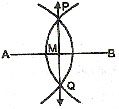
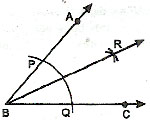
The Perpendicular Bisector of a Line segment :
In a plane, the perpendicular bisector of a segment is the line that is perpendicular to the segment at its midpoint, Line l is the perpendicular bisector of segment AB.
Construction of Perpendicular Bisector of a Segment :
Using ruler and compass, to construct the perpendicular bisector of a given line segment.
STEP 1.
Open the legs of compass to more than half the length of AB. With A as centre (i.e., place the metal-tip of compasses at A), draw arc 1.
STEP 2.
With B as centre and the same radius (i.e., the same opening of the compass), draw arc 2 to cut the first arc. Name the points of intersections as P and Q.
STEP 3.
Draw the line through P and Q by joining P, Q. This line bisects the given line segment AB and is called the bisector of AB.
Let PQ cut AB at M. Then M is called the middle point or simple midpoint of AB.
The line PQ is the perpendicular bisector or the right bisector of AB.
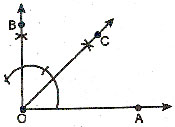
To Construct an Angle Equal to a Given Angle ABC :
STEP 1.
Draw any ray QR. This ray will become one side of the angle and its end point Q will become the vertex of the angle.
STEP 2.
Put the metal tip of your compass on the vertex of ÐABC.
Draw an arc.
STEP 3.
Without changing the opening of the compass, put the metal tip of the compass on Q. Draw an arc of sufficient length which crosses the ray as shown.
STEP 4.
Open the compass so that the metal tip and pencil point are on the points where the arc cuts the arms of ÐABC.
STEP 5.
Without changing the opening of the compass put the metal tip on the point where the arc cuts QR. Draw another arc that crosses the previous arc at, say, P.
STEP 6.
From point Q draw a ray through the intersection of two arcs, then ÐPQR = ÐABC. Check your construction with your protractor.
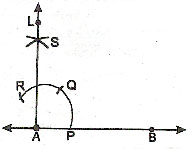
To Bisect a Given Angle ABC
STEP 1.
With B as centre and a suitable radius, draw an arc that intersects BA and BC. Name the points of intersection as P and Q.
STEP 2.
With P as centre and a radius greater than half PQ draw an arc.
STEP 3.
With Q as centre and the same radius draw another arc to cut the first arc. Name the point of intersection of the two arcs as R.
Join BR. Ray BR bisects ÐABC. Ray BR is called the angle bisector. Check your result with a protractor.
Angles of Special Measures
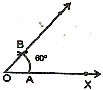
ANGLE OF 60º
STEP 1.
Draw a ray OX.
STEP 2.
With O as centre and any convenient radius draw an arc above OX, and also cutting OX at A.
STEP 3.
With A as centre and the same radius, draw another arc to cut the first arc at B.
STEP 4.
Join OB. Then ÐAOB = 60º
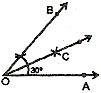
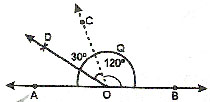
ANGLE OF 30º
STEP 1.
Draw a ray OA.
STEP 2.
With O as the vertex, construct ÐAOB of 60º.
STEP 3.
Bisect ÐAOB. OC is the bisector. Then, ÐAOC = 30º, ÐCOB = 30º
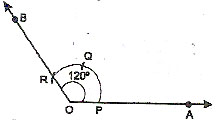
ANGLE OF 120º
STEP 1.
Draw a ray OA.
STEP 2.
With O as centre and any convenient radius draw an arc to cut OA at P.
STEP 3.
With P as centre and the same radius draw another arc to cut the first arc at Q.
STEP 4.
With Q as centre and the same radius draw another arc to cut the first arc at R.
STEP 5.
Draw the ray OB through O and R. then ÐAOB = 120º
ANGLE OF 150º
STEP 1.
Draw a line AB.
ANGLE OF 90º
STEP 2.
With any vertex O on AB, construct ÐBOC of 120º
STEP 3.
Bisect ÐAOC. Ray OD is the bisector.
Then ÐBOD = 150º
ANGLE OF 90º
STEP 1.
With A as centre and any suitable radius draw an arc cutting AB at P.
STEP 2.
With P as centre and the same radius as before cut the arc of Step 1 at Q. With Q as centre and the same radius cut the arc again at R.
STEP 3.
With Q and R as centres and any convenient radius (same for both) draw arcs cutting at S. Join A to S and produce A to L. Then ÐBAL = 90º., i.e., AL is perpendicular to AB at A.
ANGLE OF 45º
STEP 1.
Construct an angle AOB of 90º as in the previous construction.
STEP 2.
Bisect ÐAOB. Let OC be the angle bisector. Then ÐAOC = 45º; ÐCOB is also = 45º
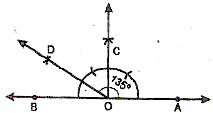
ANGLE OF 135º
STEP 1.
Draw a line AB.
STEP 2.
With any point O on line AB as vertex, construct ÐAOC = 90º. Then ÐBOC is also = 90º.
STEP 3.
Bisect ÐBOC. Ray OD is the bisector.
Then, ÐAOD = 90º + 45º = 135º
SUBJECTIVE TYPE
Q.1 Draw a circle of radius 3.5 cm.
Q.2 Draw a circle of radius 4.5 cm. with the sam centre, draw two more circles of radii 3.8 cm and 3 cm. What special name do you give to these circles ?
Q.3 Draw a circle of any radius, say 4 cm. Draw any two of its diameters. Join the ends of these diameters.
What figure do you obtained if the diameters are perpendicular to each other.
Q.4 Draw the line segments whose measure are :
(i) 7.3 cm (ii) 8.5 cm
Q.5 Construct a line segment of length 10 cm. From this cut a segment AC of length 4.6 cm. Measure the remaining segment.
Q.6 Draw a line segment AB = 8 cm. Mark a point P on AB such that AP = 4.5 cm. Draw a ray perpendicular to AB at P by
(i) Using set-squares
(ii) using compass
Q.7 Draw a line LM and take a point P not lying on it. Using set squares, construct a perpendicular from P to the line LM.
Q.8 Draw a circle of diameter 7 cm. Draw another diameter perpendicular to the first diameter. What figure is formed by joining the ends of these diameters ?
Q.9 Draw a segment of the length given. Construct its perpendicular bisector.
(a) 6 cm (b) 8.7 cm (c) 98 mm
Q.10 Draw a circle of radius 3.8 cm. Mark any three points P, Q, R on the circumference. Construct the perpendicular bisectors of PQ and QR. Where do the two bisectors meet ?
Q.11 Use a protractor to draw angles of :
(A) 48º (B) 75º (C) 122º (D) 118º
Q.12 With compasses and a ruler, construct each of the following angles :
(a) 60º (b) 30º (c) 90º (d) 45º
(e) 22 (f) 75º (g) 135º (h) 150º
(i) 120º
OBJECTIVE :
1. C 2. D 3. D 4. D
5. C 6. D 7. A 8. C
9. D 10. C 11. B 12. C
13. B 14. A 15. D 16. C
17. C 18. C 19. A 20. B
SUBJECTIVE :
1. (i) (l, m) (m, n) (l, n)
(ii) (l, r) (m, r) (n, r) (l, q) (m, q) (n, q) (p, l) (p, m) (p, n) (p, q) (p, r)
(iii) (m, p)
2.ÐDCM, ÐMCN, ÐNCB, ÐDCN, ÐMCB, ÐDCB
3.Lines which are concurrent
(i) At A are DA, CA, AB
(ii) At O are BD, AC, RP, SQ
(iii) At B are DB, CB, AB
4.(i) The side apposite to vertex P in DPQR is QR
(ii) The altitude from vertex P, in DPQR is PT
(iii) The angle opposite to side PQ, in DPQT is ÐPTQ
(iv) The vertex opposite to side PR in DPQR is Q
(v) The median from vertex P in DPQR is PS
5. (i)
(ii)
6. (i) OB, OM, OL (ii) radii, outer
(iii) diameter, inner (iv) diameter, outer
(v) concentric (vi) semicircle, inner
(vii) sector, outer
7. (i) False (ii) True (iii) True (iv) False
(v) True (vi) True (vii) True (viii) False
8. (i) Circumference (ii) Radius
(iii) Chord (iv) Center
(v) Diameter (vi) Arc
(vii) Sector (viii) Segment
9. Open figure: (i) and (iii)
Close figure: (ii), (iv) and (v)