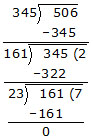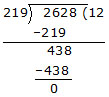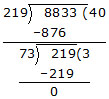FACTORS
Any number which is an exact divisor of a given number is called a factor of the given number.
For example factor of 6 are 1, 2, 3 and 6
Important results :
(a) 1 is a factor of every number.
(b) Every number is a factor of itself.
(c) Every factor of a number is always equal to or less than the number.
(d) Every number has a finite number of factors.
MULTIPLES
Just as 1, 2, 3 and 6 are factors 6, we say that 6 is multiple of 1, 2, 3 and 6
A number is a multiple of each of its factors
Important results :
(a) Every number is a multiple of itself.
(b) Every multiple of a number is equal to or greater than the number
(c) Every number has as infinite number of multiples.
TYPES OF NUMBERS
(a) Even Number : A number which is exactly divisible by 2 is called an even number.
(b) Odd Number : A number which is not exactly divisible by 2 is called an odd number.
Example of odd numbers are : 1, 13, 15, 25, 29, ...........
(c) Prime Numbers : A natural number greater than 1, which has no factors except 1 and itself is called a prime number.
Examples of prime numbers are : 2, 3, 5, 11, 13, 17, ........
NOTE:
Every even number greater than 4 can be expressed as a sum of two odd prime numbers,
e.g., 6 = 3 + 3; 18 = 5 + 13; 44 = 13 + 31.
(d) Composite Numbers : A number is composite if it has at least one factor other than 1 and itself.
Example of composite numbers are 4, 6, 8, 9, 10, 12, 14,........
NOTE:
1. 1 is neither prime nor composite.
2. Every natural number except 1 is, either a prime number or a composite number.
3. 2 is the only prime number which is even. All other prime numbers are odd.
(e) Twin primes : Pairs of prime numbers that have a difference of 2 are called twin primes.
Example of twin primes are : (3, 5), (5, 7), (11, 13), (17, 19),........
(f) Perfect Numbers : If the sum of all the factors of a number is twice the number, then number is called a perfect number. For example, 6 is a perfect number since the factors of 6 are 1, 2, 3, 6 and their sum 1 + 2 + 3 + 6 = 2 × 6.
(g) Coprime Number : Two numbers are said to be coprime if they do not have a common factor other than 1.
Examples of coprime numbers are : (8, 15); (5, 9); (2, 11)
NOTE
1. Two prime numbers are always coprime.
2. Two coprime numbers need not be both prime numbers.
(h) Prime Triplet : A set of successive prime numbers differing by 2 is called a prime triplet. The only example of a prime triplet is (3, 5, 7).
Divisibility Tests For 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
(a) Test of divisibility by 2
A number is divisible by 2 if its one’s digit is an even digit. For example 206 is divisible by 2 because 6 is even.
(b) Test of divisbility by 4
A number is divisible by 4 if the number formed by its last two digits (One’s and Ten’s) is divisible by 4. For example 312 is divisble by 4 because 12 is divible by 4.
(c) Test of divisibility by 8
A number is divisible by 8 if the number formed by its last three digits (One’s Ten’s Hundred’s) is divisible by 8. For example 8864 is divible by 8 because 864 is divisible by 8.
(d) Test of divisibility by 5
A number is divisible by 5 if its one’s digit is 0 or 5. For example 3075 is divisible by 5 because its one digit is 5.
(e) Test of divisibility by 10
A number is divisible by 10 if its one’s digit is 0.
For example 3760 is divisible by 10 because its one’s digit is 0.
(f) Test of divisibility by 3
A number is divisible by 3 if the sum of its digits is divisible by 3.
For example 567 is divisible by 3 because sum of digit of 567 (5 + 6 + 7 = 18) is divisible by 3.
(g) Test of divisibility by 9
A number is divisible by 9 if the sum of its digits is divisible by 9.
For example 4563 is divisible by 9 because sum of digit of 4563 (4 + 5 + 6 + 3 = 18) is divisible by 9
(h) Test of divisibility by 6
A number is divisible by 6 if it is divisible by both 2 and 3.
For example 456 is divisible by 6 beacuse its one’s digit is even so it is divisible by 2, and the sum of digit of 456(4 + 5 + 6 = 15) is divisible by 3. So 456 is divisible by 2 and 3 both, so we can say that it is divisible by 6.
(i) Test of divisibility by 11
A number is divisible by 11 if the difference of the sums of the digits at the alternate places is zero or divisible by 11.
For example 45672 is divisible by 11 because sum of digit 4, 6 and 2 at alternate palce 4 + 6 + 2 = 12 sum of digit 5, 7 at alternate place 5 + 7 = 12
So their difference (12 – 12 = 0) is zero, so 45672 is divisible by 11.
NOTE :
A given number will be divisible by any other number say, n, if it is divisible by the coprime factors of n.
For example, 9624 is divisible by 12, because it is divisible by 4 and 3 (the coprime factors of 12).
SIEVE OF ERATOSTHENES
How can we list all the prime number between say, 1 and 100? Eratosthenes (274 B.C. – 194 B.C.), a Greek mathematician, gave a simple method to mark out primes. His method is knows as the Sieve of Eratosthenes.
We first list the number upto 100, except 1
SIEVE OF ERATOSTHENES
1. Begin with 2 which is prime. So keep it but cross out all its multiples.
2. Next, the number 3 is prime. Thus we keep it but cross out all its multiples. Some of these numbers have already been crossed out.
3. The next number not crossed out is 5. It is also prime. So keep it and cross out all its multiples.
4. Continue this process keeping only the primes and striking off their multiples until we cannot strike off any more numbers.
Thus the prime numbers from 1 to 100 are :
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Eratosthenes, probably, made holes in the paper instead of crossing out the numbers. Therefore, his paper must have look like a sieve. That is why perhaps this method is known as sieve method.
Observations. Some observations about prime numbers are :
(i) 2 is the smallest prime number.
(ii) All prime numbers (except 2) are odd numbers.
(iii) The number of primes is unlimited.
(iv) Both the numbers 13 and 31 have the same digits and are prime. Other such numbers between 1 and 100 are : 17, 71; 37, 73 and 79, 97.
(v) Every odd prime number can be expressed as a product of primes plus 1.
For example
3 = 2 + 1; 5 = 2 × 2 + 1
7 = 2 × 3 + 1; 43 = 2 × 3 × 7 + 1
TO FIND PRIME NUMBERS BETWEEN 100 AND 400
We know that 20 × 20 = 40
So we adopt the following rule :
Rule : The given number will be prime if it is not divisible by any prime number less than 20.
Ex. Find out whether 397 is a prime number or not.
Sol. Because 397 < 400, we check whether 397 is divisible by any prime number less than 20.
The prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17, 19. Let us test the divisibility of 397 by each of them. 397 is not divisible by 2 because the digit in the ones place is odd.
397 is not divisible by 3 because 3 + 9 + 7 = 19, but 19 is not divisible by 3. 397 is not divisible by 5 because the digit in the ones place is neither 5 nor 0, 397 is not divisible by 7 because 397 ¸ 7 gives quotient 56 and remainder 5. 397 is not divisible by 11 because the difference of the sum of the digits at the alternate places is 1 which is not divisible by 11.
Now 397 is not divisible by 13 because 397 ¸ 13 gives quotient 30 and remainder 7.
397 is not divisible by 17 because 397 ¸ 17 gives quotient 23 and remainder 6.
397 is not divisible by 19 because 397 ¸ 19 gives quotient 20 and remainder 7.
Since 397 is not divisible by any prime number less than 20, so 397 is a prime number.
Prime Factorisation or Complete Factorisation
A factorisation is prime if all the factors are prime.
For example prime factorisation of 120 is
120 = 2 × 2 × 2 × 3 × 5 = 23 × 3 × 5
The prime factorisation is unique
60 = 60 × 1 = 30 × 2
= 15 × 2 × 2 = 5 × 3 × 2 × 2
In writing 60 as 5 × 3 × 2 × 2, we see that each of the factors of 60 is a prime number. When we factorise a number into prime factors, we say that we have written the prime factorisation or complete factorisation of the number.
Fundamental Theorem Arithmetic
Every composite number can be factorised into prime in only one way, except, for the order of primes.
Common Factors
Numbers which exctly divide two or more numbers are called their common factors.
All factors of 18 are : 1, 2, 3, 6, 9, 18
All factors of 24 are : 1, 2, 3, 4, 6, 8, 12, 24
Common factors of 18, 24 are : 1, 2, 3, 6 as they divide both 18 and 24.
HIGHEST COMMON FACTOR (H.C.F.)
To find highest common factor (H.C.F.) or greatest common divisor (G.C.D.) of two or more numbers, we adopt the folllowing method. Let us find H.C.F. of two numbers say 16 and 40.
All possible factors of 16 are : 1, 2, 4, 8, 16.
All prossible factors of 40 are : 1, 2, 4, 5, 8, 10, 20, 40
Now the common factors of 16 and 40 are : 1, 2, 4, 8.
The highest of all these common factors is 8.
Finding HCF by Prime Factorisation
STEP 1.
Find the prime factorisation of the given numbers.
STEP 2.
Find the common factors and circle them.
STEP 3.
Multiply the common factors to get HCF.
Let us now find the HCF of 72, 64 and 48.
STEP 1.
Find the prime factorisation of each the numbers.
We can factorise the numbers as follows :
72 = 2 × 2 × 2 × 3 × 3
64 = 2 × 2 × 2 × 2 × 2 × 2
48 = 2 × 2 × 2 × 2 × 3
STEP 2.
Take the common factors in all the given numbers.
72 = 2 × 2 × 2 × 3 × 3
64 = 2 × 2 × 2 × 2 × 2 × 2
48 = 2 × 2 × 2 × 2 × 3
STEP 3.
Multiple the common factor to get the HCF.
The HCF of 72, 64 and 48 = 2 × 2 × 2 = 8
Finding HCF using Division by Common Factors
Divide all the three numbers by any factor common to all of them. If there are till any common factors, again divide the quotients by them and keep dividing until there is no common factor for all three of them. The product of these common factors will give the highest common factor (HCF) of these number.
H.C.F. BY DIVISION METHOD
In this method, we divide the greater number by the smaller number. Then the remainder is treated as divisor and the first divisor as dividend. We continue this operation till we get the remainder zero. The last divisor is the H.C.F. of the two given number. We illustrate this method by the following exmples.
Ex. Find the H.C.F. of 345 and 506.
Sol
The last divisor is 23.
\ H.C.F. of 345 and 506 is 23.
To find the H.C.F. of three number, first we find the H.C.F. of any two numbers. Then treating this H.C.F. as one number and third number as another number, we find their H.C.F. by the method stated above. The H.C.F. so found will be the H.C.F. of the three numbers.
Ex. Find the H.C.F. of 219, 2628, 2190 and 8833.
Sol. First we find the H.C.F. of 219 and 2628.
Now we find the H.C.F. of 219 and 2190.
H.C.F. of 219, 2628 and 2190 = 219.
Now we find the H.C.F. of 219 and 8833.
Hence the H.C.F. of 219, 2628, 2190 and 8833 is 73.
Ex. Find the greatest numberthat will divide 18 and 48 without leaving a remainder.
Sol. Required number is the HCF of 18 and 48.
HCF of 18 and 48 is 6
18 = 2 × 3 × 3
48 = 2 × 2 × 2 × 2 × 3
Required HCF = 2 × 3
the greatest number that will divide 18 and 48 without leaving a remainder is 6.
Ex. Find the greatest number which divides 43 and 91 leaving a remainder 7 in each caes.
Sol. It is given that the required number when divides 43 and 91, the remainder is 7 in each case. This means that 43 – 7 = 36 and 91 – 7 = 84 are completely divisible by required number.
Also, the required number is the greatest number satisfying the above property.
\ It is the HCF of 36 and 84.
36 = 2 × 2 × 3 × 3
84 = 2 × 2 × 3 × 7
\ Required HCF = 2 × 2 × 3 = 12
Hence, the required number = 12
Ex. Find the largest number that will divide 20, 57 and 85 leaving remainders 2, 3 and 4 respecitively.
Sol. Clearly, the required number is the HCF of the number 20 – 2 = 18, 57 – 3 = 54 and 85 – 4 = 81.
18 = 2 × 3 × 3
54 = 2 × 3 × 3 × 3
81 = 3 × 3 × 3 × 3
\ Required HCF = 3 × 3 = 9
Hence, the required number = 9.
Ex. The length, breadth and height of a room are 8m 25cm, 6m 75cm and 4m 50cm resprctively. Determine the longest rod which can measure the three dimensions of the room exactly.
Sol. We have, 8m 25cm = 825cm, 6m 75cm = 675cm 4m 50cm = 450cm
Length of the longest rod in cm is the HCF of 825, 675 and 450.
825 = 3 × 5 × 5 × 11
675 = 3× 3 × 3 × 5 × 5
450 = 2 × 3 × 3 × 5 × 5
\ HCF 825, 675 and 450 = 3 × 5 × 5 = 75
Hence, the required length of rod = 75.
Ex. A rectangular courtyard 3.78 metres long and 5.25 metres wide is to be paved exactly with square tiles, all of the same size. What is the largest size of the tile which could be used for the purpose?
Sol. Largest size of the tile = H.C.F. of 378 cm and 525 cm = 21 cm.
Common Multiple
Number which are exactly divisible by two or more numbers are called their common multiples.
Let us find the common multiple of 12 and 18.
Multiples of 12 are 12, 24, 36, 48, 60, 72 .....
Multiples of 18 are 18, 36, 54, 72 .....
The common multiple of 12 and 18 are 36, 72 ....
LEAST COMMON MULTIPLE (L.C.M.)
To find LCM of two or more number we adopt the following steps :
(i) Find the multiples of the given numbers.
(ii) Select their common multiples
(iii) Take the smallest of the above common multiples
Let us find the LCM of 6 and 8
The multiple of 6 are 6, 12, 18, 24, 30, 36, 42, 48, .....
The multiple of 8 are 8, 16, 24, 32, 40, 48,.....
So common multiple of 6, 8 are 24, 48,.....
The lowest common multiple of 6 and 8 is 24
Hence 24 is the LCM of 6 and 8
Finding LCM by Prime Factorisation
STEP 1.
Find the prime factorisation of the given numbers.
STEP 2.
LCM is the product of all the prime factors with greatest powers.
Ex. Find the LCM of 84 and 96.
Sol. 84 = 2 × 2 × 3 × 7 = 22 × 3 × 7
96 = 2 × 2 × 2 × 2 × 2 × 3 = 25 × 3
LCM of 84,96 is 25 × 3 × 7 = 672
Finding LCM by common Division
STEP 1.
Write the given numbers in a row separated by commas.
STEP 2.
Divide these numbers by the least prime numbers which divides at least one of the given numbers.
STEP 3.
Write the quotients and the numbers that are not divisible by the prime numbers in the second row. Then repeat Steps 2 and 3 with the rows and continue till the numbers in a row are all 1.
STEP 4.
The LCM is found out by multiplying all the prime divisors and quotients other than 1.
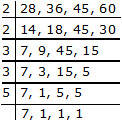
Ex. Find the L.C.M. of 28, 36, 45 and 60.
Sol.
L.C.M. = 2 × 2 × 3 × 3 × 5 × 7 = 1260
Relationship between HCF and LCM
Let us take two numbers, say 16 and 24.
The HCF of 16 and 24 is 8.
The LCM of 16 and 24 is 48.
Since 8 is factor of 48, so we can say that HCF of the numbers is a factor of their LCM.
Product of HCF and LCM = 8 × 48 = 384
Product of Numbers = 16 × 24 = 384
So we can say that the product of two numbers is equal to the product of their HCF and LCM.
Let a and b are two numbers then a × b = HCF × LCM
Ex. The HCF of two number is 29 and their LCM is 1160.
If one of the number is 145, find the other.
Sol. We know that
Product of the number = Product of their HCF and LCM
Required No. × 145 = 29 × 1160
Required No. =
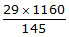
= 232
Properties of HCF and LCM
1. The HCF of 6 and 10 is 2. So 2 is a factor of both 6 and 10. Also, 2 is the smallest amongst 2, 6 and 10.
2. The LCM of 6 and 10 is 30. 30 is a multiple of both 6 and 10. Also, 30 > 10 and 6, i.e., it is the greatest amongst 6, 10 and 30.
3. Consider two numbers 36 and 39.
Now, 35 = 1 × 5 × 7
39 = 1 × 3 × 13
Common factor = 1
\ 35 and 39 are co-prime
HCF of 35 and 39 = 1
Thus HCF of two or more co-prime numbers is 1.
4. Again consider 35 and 39 which are coprime.
LCM of 35 and 39 = 3 × 5 × 7 × 13 = 35 × 39
Thus the LCM of co-prime numbers = the product of the co-primes.
5. HCF of 6, 10 = 2
LCM of 6, 10 = 30
Also, 30 = 2 × 15 = 2 × 3 × 5
i.e., 2 is a factor of LCM.
Thus, HCF is a factor of LCM. In other words, LCM is a multiple of HCF.
6. 2 and 3 are prime numbers.
HCF of 2 and 3 is 1.
HCF of two or more prime numbers is 1.
Some More Divisibility Rules
Let us observe a few more rules about the divisibility of numbers.
(i) One of the factor of 18 is 9. A factor of 9 is 3. Is 3 a factor of 18? Yes it is. Take any other factor of 18, say 6. Now, 2 is a factor of 6 and it also divides 18. Check this for the other factors of 18. Consider 24. It is divisible by 8 and the factors of 8 i.e., 1, 2, 4 and 8 also divide 24.
So, we may say that if a number is divisible by another number then it is divisible by each of the factors of that number.
(ii) The number 80 is divisible by 4 and 5. It is also divisible by 4 × 5 = 20, and 4 and 5 are co-primes.
Similarly, 60 is divisible by 3 and 5 which are coprime. 60 is also divisible by 3 × 5 = 15,
If a number is divisible by two co-prime numbers then it is divisible by their product also.
(iii) The numbers 16 and 20 are both divisible by 4. The number 16 + 20 = 36 is also divisible by 4.
If two given numbers are divisible by a number, then their sum is also divisible by that number.
(iv) The number 35 and 20 are both divisible by 5. Their difference 35 – 20 = 15 also divisible by 5.
If two given number are divisible by a number, then their difference is also divisible by that number.
Ex. Find the least number with when divided by 6, 7, 8, 9 and 10 leaves reaminder 1.
Sol. As the remainder is same
Required number = LCM of divisors + Remainder = LCM (6, 7, 8, 9, 10) + 1
= 2520 + 1 = 2521
Ex. Find the least number which when decreased by 7 is exactly divisible by 12, 16, 18, 21 and 28.
Sol.
LCM = 2 × 7 × 3 × 2 × 4 × 3 = 1008
Required number = 1008 + 7 = 1015.
Ex. When 21 is added to a number it is diveded exactily by 3, 8, 9, 12, 16 and 18. How many such numbers exist? Find the least of them.
Sol. We know that the least number divisible by 3, 8, 9, 12, 16 and 18 is their LCM.
Therefore, the required number must be 21 less then their LCM
LCM = 2 × 2 × 2 × 3 × 3 × 2 = 144
Hence, the required number = (144 – 21) = 123
There exists many such numbers (i.e., all the multiples of 123) and least of them is 123.
Ex. In a morning walk four boys steps off together. Their steps measure 70 cm, 65 cm, 75 cm and 80 cm respectively. At what distance from the starting point will they step off together again?
Sol. The distance covered by each one of them is required to be same and minimum both. The required minimum distance each should walk must be the LCM of their steps in cm.
LCM = 2 × 5 × 7 × 13 × 15 × 8 = 109200
They will step off together again after a distance of 109200 cm = 1092 m.
OPERATOR PRECEDENCE
Generally, the order in which we perform operations sequentially from left to right is : division, multiplication, additions & subtraction. This order is expressed in short as 'DMAS' where 'D' stands for division, 'M' for multiplication, 'A' for addition and, 'S' for subtraction.
Ex. Simplify : (– 20) + (– 8) ¸ (– 2) × 3
Sol. We have,
(–20) + (– 8) ¸ (– 2) × 3
= (– 20) + 4 × 3
= (– 20) + 12
= – 8.
USE OF BRACKETS
In order to simipify expression involving more than one brackets, we use the following steps.
STEP 1.
See whether the given expression contains a vinculum or not. If a vinculum is present, then perform operations under it. Otherwise go to next step.
STEP 2.
See the innermost bracket and perform operations within it.
STEP 3.
Remove the innermost bracket by using following rules :
Rule 1 : If a bracket is preceded by a plus sign, remove it by writing its terms as they are.
Rule 2 : If a bracket is preceded by minus sign, change positive signs within it to negative and
vice-versa.
Rule 3 : If there is no sign between a number and a grouping symbol, then it means multiplication.
Rule 4 : If there is a number before some brackets then we multiply the number inside the bracktes with the number outside the brackets.
STEP 4.
See the next innermost bracket and perform operations within it. Remove the second
innermost bracket by using the rules given in step III. Continue this process till all the brackets are removed.
Ex. Simiplify
(i) 39 – [23 – {29 – (17 – )}]
(ii) 15 – (–3) {4 – } ¸ [3 {5 + (– 3) × (– 6)}]
Sol. (i) 39 – [23 – {29 – (17 – 6)}]
= 39 – [23 – (29 – 11)]
= 39 – [23 – 18]
= 39 – 5
= 34
(ii) 15 – (– 3) {4 – 4} ¸ [3 {5 + 18}]
15 – (– 3) × 0 ¸ 89
15 – (– 3) × 0 = 15
.JPG)