INTRODUCTION
In Arithmetic, numerals 1, 2, 3, 4,..... etc. and four fundamental operation : addition, subtraction, multiplication and division are used to deal with various problems. In Algebra, in addition to numerals, we use letters such as x, y, z in various situations to solve the problems.
MATCHSTICK PATTERN
Salman and Aamir are making pattern with matchsticks. They decide to make simple patterns of the letters of the english alphabet. Salman takes two matchsticks and form the letter L as shown in figure 1. The Aamir also picks two sticks form another letter L and puts it next to the one made by salman as shown in figure 2. The Salman adds one more L and this goes on as shown in figure 3.
If we tabulate this result we obtained the following table as given below
Here we observe that number of matchstick required is twice the number's of L
So, we can say number of matchstick required = 2 × n, where n represent the number of L's
Consider the following statements :
I think of a number and when I subtract 9 from it the result is 23.
If

is used to represent the number I think of, then the above statement using mathematical symbols, is simply written as

– 9 = 23.
Ex. Use

, D etc. and mathematical symbols and rewrite the following statements :
(a) I think of a number, subtract 3 from it and the result is 34.
(b) I think of two numbers, add these numbers, multiply the result by 2 to get the final answer as 14.
(c) I think of two numbers. Twice difference is added by 3 gives result 15.
Sol. (a)

– 3 = 34
(b) 2 × (

+ D) = 14
(c) 2 × (

– D) + 3 = 15
Ex. Rewrite each of the following statements without using symbols, beginning each statement with : I think of .....
(a)

+ 9 = 28
(b) 2 ×

– 23 < 25
(c) (

+ D) ¸ 5 = 25
Sol. (a) I think of a number, when 9 is added to it gives result 28.
(b) I think of a number, when 23 is subtracted from the twice the number gives the result is less than 25.
(c) I think of two numbers, when their sum is divided by 5 gives quotient 25.
LITERAL NUMBERS
We have mentioned earlier that the letters represent the numbers. These letters are called literal numbers and obey all the rules of arithmetic.
NOTE
5 × p × q = 5pq. 5, p and q are factors of 5pq, 5 is a numerical factor and p, q are literal factors.
Ex. Give expressions for the following cases.
(a) Rita scores x marks in Maths and 46 marks in English. What is her total score in Maths and English.
(b) The difference of x and 9 where x > 9.
(c) The product of a and b added to the difference of a and b(a > b).
(d) One-half of a multiplied by the sum of x and y.
(e) The total distance travelled by a car in x hours at a constant speed of y km/h.
(f) The total number of eggs in n cartons if each carton contains k eggs.
Sol. (a) Total marks = x + 46
(b) x – 9
(c) ab + a – b
(d) a/2 × (x + y)
(e) distance = (x × y) Km.
(f) Number of eggs = (n × k) eggs
Ex. Ali is x years old. Express the following in algebraic form :
(a) Ali's age 5 years ago
(b) Ali's age 2 years from now
(c) 4 times Ali's age 3 years hence.
(d) the present age of Ali's aunt who is four times as old as Ali will be 5 years from today.
(e) The present age of Ali's father who is 5 times as old as Ali was 3 years ago.
Sol. (a) Ali's age 5 years ago = (x – 5) years
(b) Ali's age 2 years from now = (x + 2) years
(c) Ali's age 3 years hence = (x + 3) years 4 times Ali's age 3 years hence = 4(x + 3) years
(d) Ali's age after 5 years = (x + 5) years Ali's aunt age = 4(x + 5) years
(e) Ali's age before 3 years = (x – 3) years Ali's father age = 5(x – 3) years
POWERS OF LITERAL NUMBERS
We have read earlier that 2 × 2 × 2 = 23 and (– 3) × (– 3) = (– 3)2
Similarly, a × a × a = a3 and (– y) × (– y) × (– y) × (– y) = (– y)4
a3 is read as 'a to the power three' or 'a raised to the power three' or 'a cube' or 'third power of a' and (– y)4 is read as '– y to the power four' or '– y raised to the power four' or fourth power of – y'.
In a3, a is called base and 3 is called exponent or index.
COEFFICIENT
The number expressed in figures or symbols, standing before an algebraic term as a multiplier is called its coefficient. Thus in 3abc, 3 is the coefficient of abc, 3a is the coefficient of bc and 3ab is the coefficient of c. When one of the factors is an Airthmetic number it is always written first and is called a numerical coefficient. Thus in 3xyz, 3 is the numerical coefficient of xyz. When the coefficient is expressed in letter, it is called a literal coefficient is expressed in letter, it is called a literal coefficient. Thus in axy a is the literal coefficient of xy. When the coefficient is 1 or – 1, the number 1 is usually omitted. Thus 1 x is written as x and – 1 x as – x, 1xy is written as xy and – 1 xy as – xy.
VARIABLES AND CONSTANTS
In algebra we come across two types of symbols, namely variables and constants. A symbol having a fixed value is called a constant whereas a symbol which takes on various numerical values is called a variable.
For example, the perimeter p of rectangle is given by the formula p = 2(l + b), where l and b are its length and breadth. Here 2 is a fixed number and hence a constant but the literal numbers p, l and b depends on different sizes of the rectangle and hence they are variables.
Ex. Write down the coefficient of :
(a) x in 3xy (b) abc in –5abc (c) y in 2xyz (d) a2 in – a2bc
Sol. (a) 3y (b) –5 (c) 2xz (d) – bc
Ex. Write down the numerical coefficinet in each of the following :
(a) 5 ab (b) – 3xyz (c) px (d) – y
Sol. (a) 5 (b) – 3 (c) 1 (d) – 1
ALGEBRAIC EXPRESSION
Any combination of letters or of numerals and letters connected by the symbols +, –, ×, ¸ is called an Algebraic expression. For example, 2x – 3y + 5z is an algebraic expression.
The several parts of an expression connected by the signs + and – are called the terms of the expression.
NOTE :
Only the signs + and – separate the terms of an expression. 5xy is one term whereas x – y are two terms x and –y.
An expression consisting of one term is called a monomial. 2x, 5ab, – 7xy, 20 are all examples of monomials. An expression consisting of two terms is called a Binomial. Some example of the binomials are 2x – 3y, 5a – 2b, p + 2q etc. An expression consisting of three terms is called a trinomial.
The expresion consisiting of several terms is called multinomial or polynomial expression.
Ex. Ruchika buys 5 copies for Maths, 2x copies for English and y2 copies for Hindi. Express the total number of copies she buys as an algebraic expression.
Sol. Number of copies for Maths = 5
Number of copies for English = 2x
Number of copies for Hindi = y2
Total number of copies = 5 + 2 + y2
Ex. Write the following, using symbols :
(i) a increased by twice b
(ii) three times the difference of 30 and c
(iii) 70 increased by the quotient of x and y
(iv) length in centimetres that is 4 cm longer than y metres
Sol. (i) a + 2b
(ii) 3(30 – c)
(iii) 70 +x/y
(iv) 100y + 4 (y metres = 100 × y = 100 y cm)
Ex. Write down separately the terms of the following algebraic expression :
(a) 3x – 4y
(b) 2ab + 4ac2 – 6z
(c) 7xyz + 2yz – 8x2y3
(d) –2pq2 + 7qr4 – 3p + 4p2q3r4
Sol. (a) 3x, – 4y
(b) 2ab, 4ac2, – 6z
(c) 7xyz, 2yz, – 8x2y3
(d) – 2pq2, 7qr4, – 3p, 4p2q3r4
Ex. Write down the algebraic expression whose terms are given below :
(a) 2a, – 3b, – 4c
(b) 5bc2, – 2ab, 7a2c
(c) 3t2uw3, 7t2w2 – 2p2q + 7
Sol. (a) 2a – 3b – 4c
(b) 5bc2 – 2ab + 7a2c
(c) 3t2uw3 + 7t2w2 – 2p2q + 7
Ex. Separate monomials, binomials and trinomials from the following :
5x2 – 3xy, 2x4, 3x – 2y + 4z, –3y2, 5x3y2 + 4y2z – z5, ax – by + cz2, pq + rst
Sol. Monomials are 2x4, – 3y2
Binomials are 5x2 – 3xy, pq + rst
Trinomials are : 3x – 2y + 4z, 5x3y2 + 4y2z – z5, ax – by + cz2
Ex. If a = 2, b = 3, c = 4, find the value of :
(a) a + b + c
(b) 2c – b – a
(c) 3a – b + 2c
(d) a2 – b2 + c2
(e) ab – 3abc – 2ac
(f) a2b + bc – 3c3 – 2abc
Sol. (a) a + b + c = 2 + 3 + 4 = 9
(b) 2c – b – a = 2 × 4 – 3 – 2
= 8 – 3 – 2 = 3
(c) 3a – b + 2c = 3 × 2 – 3 + 2 × 4
= 6 – 3 + 8 = 11
(d) a2 – b2 + c2 = 22 – 32 + 42
= 4 – 9 + 16 = 11
(e) ab – 3abc – 2ac = 2 × 3 – 3 × 2 × 3 × 4 – 2 × 2 × 4
= 6 – 72 – 16 = –82
(f) a2b + bc – 3c3 – 2abc
= 22 × 3 + 3 × 4 – 3 × 43 – 2 × 2 × 3 × 4
= 12 + 12 – 192 – 48 = – 216
ALGEBRAIC EQUATIONS
An equation is a mathematical statement equating two quantities. The expressions on either side of the equal sign (=) are called members of the equation. In an equation, the value of the quantity which is not known is referred to as the unknown member or the unknown. Here are some examples of equations.
2x + 3 = 11 x – 3 = 8 y + 3 = 21
Ex. Rewrite the following statements by using symbols wherever needed.
(i) a exceeds b by 10
(ii) Twice the product of p and q divided by r.
(iii) x is not equal to two times y.
(iv) Four times m is greater than seven.
(v) The excess of 15 over 10 is 5.
(vi) Since two times x equal sixteen, therefore x is equal to eight.
(vii) Since four into y equal forty, therefore y equals ten.
(viii) Twice the product of p and q upon the sum of a and b equal five.
(ix) The difference of x and y is less the sum of two and ten.
(x) Nine times two is greater than ten.
Sol. (i) a – b = 10 (ii) 2pq/r
(iii) x ¹ 2y (iv) 4m > 7
(v) 15 – 10 = 5 (vi) Since 2x = 16 x = 8
(vii) Since 4y = 40 y = 10 (viii) 2pq/a+b = 5
(ix) x – y < 2 + 10 (x) 9 × 2 > 10
SOLVING AN EQUATION
To solve an equation is to determine the value (s) of the variable (or unknown) that balances the equation. That value(s) is called the root (s) of the equation or solution of the equation.
Let us take an example.
x + 7 = 15 ;
We have to find the value of x which will satisfy the equation. And we observe that if we put x = 8 in this equation it will satisfy the equation. So x = 8 is the solution or root of this equation.
SOLUTION OF AN EQUATION BY TRIAL AND ERROR
One of the simplest ways of solving an equation is by the trial-and-error method. In this, a guess is made about the value of x, and this value is then substituted in the equation to check if it is the root of the equation.
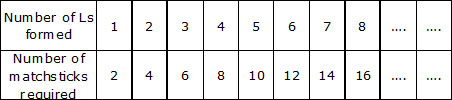
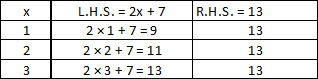
Consider the following example : 4x + 3 = 23
Our equation is 4x + 3 = 23. So we substitute different values for x and try to find out which value of x will satisfy the equation. Make a chart as follow.
When x = 5, 4x + 3 = 23 so the root of the equation or the solution of the equation 4x + 3 = 23 is 5.
Ex. Determine if 3 is the root of the equation 5x – 10 = 5.
Sol. If we put x = 3, then L.H.S. = 5x – 10
= 5 × 3 – 10
= 15 – 10 = 5
R.H.S. = 5
L.H.S. = R.H.S.
Thus, 3 is a root of the given equation.
Ex. Express the following as algebraic equation and solve.
(a) Twice a number increased by 7 is 13. What is the number?
(b) Seven times a number decreased by 4 is 10. Find the number
Sol. (a) Let the number be x
Twice the number = 2x
2x + 7 = 13
Thus for x = 3, L.H.S. = R.H.S.
So the required number is 3.
(b) Let the numbers be x.
7x – 4 = 10
Here for x = 2, L.H.S. = R.H.S.
The required number is 2.
Ex. If 20 is subtracted from a number, is result is 45.
Convert this statement into an algebraic equation.
Sol. Let us suppose that x is the unknown number,
Then x – 20 stands for 20 subtracted from the number x. This is equal to 45.
Hence, x – 20 = 45
Once you convert statement into an algebraic equation, it is easier to solve and find the root.
Ex. Sunny is twice as old as Manoj. Convent this statement into an algebraic equation.
Sol. Let sunny's age be s and Manoj's age be m. Twice Manoj's age is 2m.
Hence, the equation is s = 2m.
SYSTEMATIC METHOD
A much better method of solving an equation is the systematic method as the trial and error method could take a lot of time.
Property -1 : We can add the same number to both sides of the equation;
Ex. Solve the equation x – 7 = –2 and check the result.
Sol. We have, x – 7 = –2.
In order to solve this equation, we have to get x by itself on the L.H.S., We need to shift – 7. This can be done by adding 7 to both sides of the given equation.
Thus,
x – 7 = – 2
⇒ x – 7 + 7 = –2 + 7 [Adding 7 to both sides]
⇒ x + 0 = 5 [Q –7 + 7 = 0 and –2 + 7 = 5]
⇒ x = 5
Thus, x = 5 is the solution of the given equation.
L.H.S. = 5 – 7 = –2 and R.H.S. = – 2
Thus, when x = 5, we have L.H.S. = R.H.S.
Property-2 : We can subtract the same number from both sides of the equation.
Ex. Solve the equation x + 4 = –2 and check the result
Sol. In order to solve this equation, we have to obtain x by itself on L.H.S. To get x by itself on L.H.S., we need to shift 4. This can be done by subtracting 4 from both sides of the given equation.
Thus, x + 4 = –2
⇒ x + 4 – 4 = –2 –4 [Subtracting 4 from both sides]
⇒ x + 0 = –6 [Q 4 – 4 = 0 and –2 –4 = –6]
⇒ x = –6
Thus, x = –6 is the solution of the given equation.
Property-3 : We can multiply both sides of the equation by same non-zero number.
Ex. Solve the equation y/12= 48 and check the result.
Sol. In order to solve this equation, we have to get y by itself on L.H.S. To get y by itself on L.H.S., we have to remove 12 from L.H.S. This can be done by multiplying both sides of the equation by 12 thus, we have
y/12= 48
y/12 × 12 = 48 × 12 [Multiplying both sides by 12]
⇒ y = 576
Check : Putting, y = 576 in the given equation, we get L.H.S. =576/12 = 48 and R.H.S. = 48.
Thus, for y = 567, we have L.H.S. = R.H.S.
(iv) We can divide both sides of the equation by the same non-zero number.
Ex. Solve the equation 2/3 x = 18 and check the result.
Sol. We have,
2/3x = 18
Multiplying both sides by
⇒ 2/3×3/2× x = 3/2× 18
Thus, for x = 27 is solution of given equation.
Property -4 : In an equation, we can drop a term from one side and put it on the other side with the opposite sign. This process is known as transposition.
Ex. Solve : 3(x + 3) – 2 (x – 1) = 5 (x – 5).
Sol. We have,
3(x + 3) – 2 (x – 1) = 5 (x – 5)
⇒ 3x + 9 – 2x + 2 = 5x – 25 [Expanding brackets on both side]
⇒ 3x – 2x + 9 + 2 = 5x – 25
⇒ x + 11 = 5x – 25 [Taking 5x to the L.H.S. and 11 to the R.H.S.]
⇒ –4x = –36
x = 9
OBJECTIVE TYPE
Q.1 Which of the following is monomial
(A) x+y+z (B) 2xy (C) p+q+r+s (D) 2x-3
Q.2 The algebraic expression for the statement : Twice a number p plus 3 is 17 is:
(A) p+3=17 (B) 2+p+3=17 (C) 2p+3 =17 (D) 2p-3=17
Q.3 The algebraic expression of the statement 'product of numbers a and b subtracted from 7' is :
(A) ab- 7 (B) 7- ab (C) ab (D) 7ab
Q.4 Value of x2- xy + y2 when x = 0 & y =1 is :
(A) -1 (B) 0 (C) 1 (D) 4
Q.5 The numerical coefficient of – 7xyz
(A) 7 (B) -7 (C) 1 (D) - 1
Q.6 The coefficient of r of 2pqr
(A) 2 (B)pq (C) 2pq (D) 2pqr
Q.7 Write 2 x p x p x p x q x q in exponential form
(A) 2pq (B) 2p3q2 (C) 2p2q2 (D) 2p3q3
Q.8 Solve for x : 3/5 x = 27
(A) 9 (B) 45 (C) 5 (D) 54
Q.9 Solve for x : 7x – 19 = 30
(A) 7 (B) 9 (C) 11 (D) 13
Q.10 Solve for x : 2 (x + 7) = 5 (7 – x)
(A) 3 (B) 6 (C) 9 (D) 2
Q.11 7 less than a number x is :
(A) x + 7 (B) 7 – x (C) x – 7 (D) – x + 7
Q.12 Exponential form of P × P × P × _ _ _ _ 9 times is :
(A) 9P (B) 9 + P (C) P9 (D) 3P3
Q.13 For what value of x, x + 9 = 7?
(A) 2 (B) 3 (C) – 2 (D) 4
Q.14 Mathematical form of statement "Five times a number is equal to 65" is :
(A) x = 5 × 65 (B) x + 5 = 65 (C) 5x = 65 (D) None of these
Q.15 The cost of 1 pen is Rs y, then cost of 5 pens is :
(A) y + 5 (B) 5y (C) y + 5 (D) y – 5
Q.16 6 taken away from the product of x andy is written as:
(A) 6-xy (B) 6-(x+y) (C) xy- 6 (D) (x + y)- 6
Q.17 Which verbal expression does not match the algebraic expression 13x ?
(A) 13 times x (B) x multiplied by 13
(C) 13 made into x groups (D) the product of x and 13
Q.18 Which equation has a solution - 3?
(A) x-3 = 6 (B) 6 + x = 3 (C) x- 6 = 3 (D) x- 6 =- 3
Q.19 For what value of x, x + 9 = 7 ?
(A) 2 (B) 3 (C) -2 (D) 4
Q.20 The sum of 3 times a number plus -7 is 14. What is that number ?
(A)6 (B) -7 (C) 7 (D) -6
SUBJECTIVE TYPE
Q.1 Find the rule which gives the number of matchsticks required to make the following matchsti.6k patterns.
Use a variable to write the rule.
(i) a pattern of Z as
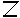
(ii) a pattern of S as
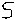
Q.2 In the given matchstick pattern of triangle. Find the general rule that gives number of matchsticks in terms of the number of triangles.
Q.3 Use

, D etc. and mathematical symbols and rewrite the following statements :
(i) I think of a number, add 2 to it and the result is greater than 8.
(ii) I think of two numbers. Twice the first number added to 3 times the second number gives a result of 23.
Q.4 Rewrite each of the following statements without using symbols, begining each statement with : I think of .......
(i) (

+ 3) > 9
(ii) (

+ 5) × D = 21
Q.5 Give expressions for the following cases.
(i) Five times b added to 3 times c.
(ii) The quotient of x and y, if x is divided by y, added to the product of x and y.
(iii) The perimeter of a rectangle is twice the sum of its length and breadth.
(iv) The distance covered is product of speed and time.
Q.6 Write down the coefficient of :
(i) x in – 8xyz (ii) ab in 7abc
(iii) z in 8xyz (iv) a2 in – 7a2bc
Q.7 Write down the numerical coefficient in each of the following :
(i) – 9xyz (ii) ab
(iii) –pqr (iv) –8y
Q.8 Shinchan went to market. He buys 2x kg of tomato, 7y kg of potato, z2 kg of onion. How many kg of vegetable he bought.
Q.9 Write down separately the terms of the following algebraic expression.
(i) 7p – 8q
(ii) 9 + abc – 2c
Q.10 Write down the algebraic expressions whose terms are given below :
(i) 3x, – 4y, 5z (ii) 7xy2, –8yz, 7x2z
Q.11 Separate monomials, binomials and trinomials from the following :
abc, a + b + c, ab + c, 2x – 3y + 5z, 4xy + 1, 7
Q.12 If A = 2, B = –1, C = –3, find the value of :
(i) A + B – C
(ii) (A + B) (B + C) (C + A)
(iii) (A – B) (B – C) (C – A)
Q.13 Find the solution of 5x – 3 = 17 using trial and error method :
Q.14 Is x = 3 is the solution of equation 5x – 7 = 6
Q.15 Solve for x :
(i) 5x + 7 = 27
(ii) 9x – 5 = 3 (x + 7) – 20
Q.16 Write the given statements in the mathematical form using signs and symbols :
(i) Two times six equals twelve.
(ii) Twelve divided by x, equals three.
(iii) Ten decreased by three equals seven.
(iv) a plus b minus c equals two.
(v) Five is greater than p.
Q.17 State the following in words :
(i) 7 + 3 (ii) 3 – 4 + 5 (iii) a + b – c
(iv) 5 × 4 (v) p × q × r (vi) x×z/y
Q.18 Write the following in exponential form :
(i) p × p × p × - - - - 11 times
(ii) a × a × a × - - - - 21 times
(iii) 14 × p × p × p × p × q
(iv) 7 × x × x × x × x × y × y
Q.19 Write down the following in product form :
(i) x3y4 (ii) 7y6 (iii) 8xy2z3 (iv) 11a4b4c4
Q.20 Write each of the following statements as an equation :
(i) A number increased by 10 equals 26
(ii) Five times a number is equal to 65.
(iii) Thrice a number decreased by 5 is equal to 27
(iv) If a number is doubled and 30 subtracted from the result, we get 56.
(v) The sum of three consecutive integers is 34.
Q.21 Write a statement for each of the equations given below :
(i) 5x = 40 (ii) x + 8 = 15 (iii) 25 – x = 7 (iv) x – 5 = 3
Q.22 Verify by substitution that :
(i) The root of 3x + 4 = 13 is 3.
(ii) the root of 5x – 8 = 7 is 3.
(iii) The root of 4x/7– 12 = 0 is 21.
(iv) The root of 3x = 20/7 – x is 5/7
Q.23 Solve the following equations by the trial and error method :
(i) x + 7 = 12 (ii) x – 15 = 20 (iii) 5x = 30
Q.24 Solve the given equation :
(i) x + 6 = 2 (ii) a – 3 = 4 (iii) x + 3 = 6
(iv) a – 2 = 0 (v) 1 = y – 7 (vi) 7x – 6 = 1
Q.25 Solve the given equations :
(i) m/2 = 5 (ii) 3x + 2 = 8 (iii) 4x – 3 = 5
(iv) 6a + 6 = 12 (v) –2x + 4 = –8 (vi) a + 6 = 8 + 1/2
OBJECTIVE :
1. B 2. C 3. B 4. B
5. B 6. C 7. B 8. B
9. A 10. A 11. C 12. C
13. C 14. C 15. B 16. C
17. C 18. B 19. C 20. C
SUBJECTIVE :
1. (a) No of matchsticks required = 3a
where a = no. of
.JPG)
(b) No of matchsticks required = 5a
where a = no. of
.JPG)
2. No. of matchsticks required = 2n + 1
Where n = no. of triangles
3. (i)

+ 2 > 8 (ii) 23
4. (i) I think of a number, when 3 in added to it the result is more than 9
(ii) I think of two no. when 5 is added to first and then it multiplied with second given product 21.
5. (i) 5b + 3c (ii) x/y+xy
(iii) P = 2(l + b) (iv) d = s × t
6. (i) –8yz (ii) 7c (iii) 8xy (iv) –7bc
7. (i) –9 (ii) 1 (iii) –1 (iv) –8
8. (2x + 7y + z2) kg
9. (i) 7p, –8q (ii) 9, abc, –2c
10. (i) 3x – 4y + 5z (ii) 7xy2 – 8yz + 7x2z
11. Monomials are : abc, 7
Binomials are : ab + c, 4xy + 1
Trinomials are: a + b + c, 2x – 3y + 5z
12. (i) 4 (ii) 4 (iii) –30
13.

14. 6
15. (i) 4 (ii) 1
16. (i) 2 × 6 = 12 (ii) 12 ÷ x = 3
(iii) 10 – 3 = 7 (iv) a + b – c = 2
(v) 5 > p
17. (i) seven plus three
(ii) Three minus four plus five
(iii) a plus b minus c
(iv) product of five and four
(v) product of p, q and r
(vi) product of x and z divided by y
18. (i) p11 (ii) a21
(iii) 14p4 + q (iv) 7x4y2
19. (i) x × x × x × y × y × y× y
(ii) 7 × y × y × y × y × y × y
(iii) 8 × x × y × y × z × z × z
(iv) 11 × a × a × a × a × b × b × b × b × c × c × c × c
20. (i) x + 10 = 26
(ii) 5x = 65
(iii) 3x – 5 = 27
(iv) 2x – 30 = 56
(v) x + (x + 1) + (x + 2) = 34
21. (i) five times a number equals 40
(ii) a number increased by 8 equals 15
(iii) 25 exceeds a number by 7
(iv) 5 subtracted from thrice a number is 16
23. (i) 5 (ii) 35 (iii) 6
24. (i) –4 (ii) 7 (iii) 3
(iv) 2 (v) 8 (vi) 1
25. (i) 10 (ii) 2 (iii) 2
(iv) 1 (v) 6 (vi) 2 1/2
In questions 1 to 23, out of the four given options, only one is correct. Write the correct answer.
1. If each match box contains 50 matchsticks, the number of matchsticks required to fill n such boxes is
(A) 50 + n (B) 50÷n (C) 50n (D) 50 – n
2. Amulya is x years of age now. 5 years ago her age was
(A) (5 – x) years (B) (5 + x) years (C) (x – 5) years (D) (5 x) years
3. Which of the following represents 6 ×
(A) 6x (B) x/6 (C) 6 + x (D) 6 – x
4. Which of the following is an equation?
(A) x + 1 (B) x – 1 (C) x – 1 = 0 (D) x + 1 > 0
5. If x takes the value 2, then the value of x + 10 is
(A) 20 (B) 12 (C) 5 (D) 8
6. If the perimeter of a regular hexagon is x metres, then the length of each of its sides is
(A) (x + 6) metres (B) (x÷ 6) metres
(C) (x – 6) metres (D) (6 ÷x) metres
7. Which of the following equations has x = 2 as a solution?
(A) x + 2 = 5 (B) x – 2 = 0 (C) 2x + 1 = 0 (D) x + 3 = 6
8. For any two integers x and y, which of the following suggests that operation of addition is commutative
(A) x + y = y + x (B) x + y > x (C) x – y = y – x (D) x × y = y × x
9. Which of the following equations does not have a solution in integers?
(A) x + 1 = 1 (B) x – 1 = 3 (C) 2x + 1 = 6 (D) 1 – x = 5
10. In algebra, a × b means ab, but in arithmetic 3 × 5 is
(A) 35 (B) 53 (C) 15 (D) 8
11. In algebra, letters may stand for
(A) known quantities (B) unknown quantities
(C) fixed numbers (D) none of these
12. “Variable” means that it
(A) can take different values (B) has a fixed value
(C) can take only 2 values (D) can take only three values
13. 10 – x means
(A) 10 is subtracted x times (B) x is subtracted 10 times
(C) x is subtracted from 10 (D) 10 is subtracted from x
14. Savitri has a sum of Rs x. She spent Rs 1000 on grocery, Rs 500 on clothes and Rs 400 on education, and received Rs 200 as a gift. How much money (in Rs) is left with her?
(A) x – 1700 (B) x – 1900 (C) x + 200 (D) x – 2100
15. The perimeter of the triangle shown in Figure is
(A) 2x + y (B) x + 2y (C) x + y (D) 2x – y
16. The area of a square having each side x is
(A) x x (B) 4x (C) x + x (D) 4 + x
17. The expression obtained when x is multipled by 2 and then subtracted from 3 is
(A) 2x – 3 (B) 2x + 3 (C) 3 – 2x (D) 3x – 2
18. q/2=3has a solution
(A) 6 (B) 8 (C) 3 (D) 2
19. x – 4 = – 2 has a solution
(A) 6 (B) 2 (C) – 6 (D) – 2
20. 4/2=2denotes a
(A) numerical equation (B) algebraic expression
(C) equation with a variable (D) false statement
21. Kanta has p pencils in her box. She puts q more pencils in the box. The total number of pencils with her are
(A) p + q (B) pq (C) p – q (D)
22. The equation 4x = 16 is satisfied by the following value of x
(A) 4 (B) 2 (C) 12 (D) –12
23. I think of a number and on adding 13 to it, I get 27. The equation for this is
(A) x – 27 = 13 (B) x – 13 = 27 (C) x + 27 = 13 (D) x + 13 = 27
In question 24 to 40, fill in the blanks to make the statements true:
24. The distance (in km) travelled in h hours at a constant speed of 40km per hour is __________.
25. p kg of potatoes are bought for Rs 70. Cost of 1kg of potatoes (in Rs) is __________.
26. An auto rickshaw charges Rs 10 for the first kilometre then Rs 8 for each such subsequent kilometre. The total charge (in Rs) for d kilometres is __________.
27. If 7x + 4 = 25, then the value of x is __________.
28. The solution of the equation 3x + 7 = –20 is __________.
29. ‘x exceeds y by 7’ can be expressed as __________.
30. ‘8 more than three times the number x’ can be written as __________.
31. Number of pencils bought for Rs x at the rate of Rs 2 per pencil is __________.
32. The number of days in w weeks is __________.
33. Annual salary at r rupees per month alongwith a festival bonus of Rs 2000 is __________.
34. The two digit number whose ten’s digit is ‘t’ and units’s digit is ‘u’ is __________.
35. The variable used in the equation 2p + 8 = 18 is __________.
36. x metres = __________ centimetres
37. p litres = __________ millilitres
38. r rupees = __________ paise
39. If the present age of Ramandeep is n years, then her age after 7 years will be __________.
40. If I spend f rupees from 100 rupees, the money left with me is __________ rupees.
In question 41 to 45, state whether the statements are true or false.
41. 0 is a solution of the equation x + 1 = 0
42. The equations x + 1 = 0 and 2x + 2 = 0 have the same solution.
43. If m is a whole number, then 2m denotes a multiple of 2.
44. The additive inverse of an integer x is 2x.
45. If x is a negative integer, – x is a positive integer.
46. 2x – 5 > 11 is an equation.
47. In an equation, the LHS is equal to the RHS.
48. In the equation 7k – 7 = 7, the variable is 7.
49. a = 3 is a solution of the equation 2a – 1 = 5
50. The distance between New Delhi and Bhopal is not a variable.
51. t minutes are equal to 60t seconds.
52. x = 5 is the solution of the equation 3x + 2 = 20
53. ‘One third of a number added to itself gives 8’, can be expressed as
54. The difference between the ages of two sisters Leela and Yamini is a variable.
55. The number of lines that can be drawn through a point is a variable.
In questions 56 to 74, choose a letter x, y, z, p etc...., wherever necessary, for the unknown (variable) and write the corresponding expressions:
56. One more than twice the number.
57. 20oC less than the present temperature.
58. The successor of an integer.
59. The perimeter of an equilateral triangle, if side of the triangle is m.
60. Area of the rectangle with length k units and breadth n units.
61. Omar helps his mother 1 hour more than his sister does.
62. Two consecutive odd integers.
63. Two consecutive even integers.
64. Multiple of 5.
65. The denominator of a fraction is 1 more than its numerator.
66. The height of Mount Everest is 20 times the height of Empire State building.
67. If a note book costs Rs p and a pencil costs Rs 3, then the total cost (in Rs) of two note books and one pencil.
68. z is multiplied by –3 and the result is subtracted from 13.
69. p is divided by 11 and the result is added to 10.
70. x times of 3 is added to the smallest natural number.
71. 6 times q is subtracted from the smallest two digit number.
72. Write two equations for which 2 is the solution.
73. Write an equation for which 0 is a solution.
74. Write an equation whose solution is not a whole number.
In questions 75 to 84, change the statements, converting expressions into statements in ordinary language:
75. A pencil costs Rs p and a pen costs Rs 5p.
76. Leela contributed Rs y towards the Prime Minister’s Relief Fund. Leela is now left with Rs (y + 10000).
77. Kartik is n years old. His father is 7n years old.
78. The maximum temperature on a day in Delhi was poC. The minimum temperature was (p – 10)oC.
79. John planted t plants last year. His friend Jay planted 2t + 10 plants that year.
80. Sharad used to take p cups tea a day. After having some health problem, he takes p – 5 cups of tea a day.
1. (B) 2. (C) 3. (A) 4. (C) 5. (B) 6. (B) 7. (B) 8. (A) 9. (C) 10. (C)
11. (B) 12. (A) 13. (C) 14. (A) 15. (A) 16. (A) 17. (C) 18. (A) 19. (B) 20. (A)
21. (A) 22. (A) 23. (D) 24. 40h 25. 70/p 26. 8d + 2 27. 3 28. – 9 29. x = y + 7 30. 3x + 8 31. x/2 32. 7w
33. 12x + 2000 34. 10t + u 35. p 36. 100x 37. 1000p 38. 100x 39. n + 7 40. 100 – f 41. F 42. T
43. T 44. F 45. T 46. F 47. T 48. F 49. T 50. T 51. T 52. F
53. F 54. F 55. F 56. 2x + 1 57. t – 20 58. n + 1 59. 3m 60. kn 61. x + 1 62. 2n + 1 and 2n + 3
63. 2m and 2m + 2 64. 5n 65. x/x+1 66. 20y, where y is height of Empire State Building. 67. 2p + 3 68. 13 – (–3) z (=13+3z)
69. 70. 3x + 1 71. 10 – 6 q 72. 3y + 4 = 10, 2x – 3 = 1 73. 2t + 3 = 3 74. x + 1 = 0

 + D) = 14
+ D) = 14

 , D etc. and mathematical symbols and rewrite the following statements :
, D etc. and mathematical symbols and rewrite the following statements : + 3) > 9
+ 3) > 9 + 5) × D = 21
+ 5) × D = 21 + 2 > 8 (ii) 23
+ 2 > 8 (ii) 23