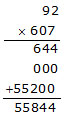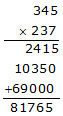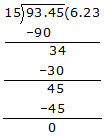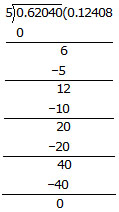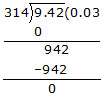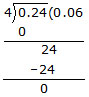DECIMALS
Decimals : Decimals are an extension of our number system. Decimals are fractions whose denominators are 10, 100, 1000 etc. A decimal has two parts, namely, the whole number part and decimal part.
Decimal Places : The number of digits contained in the decimal part of a decimal number is known as the number of decimal places.
For :
3.75 has two decimal places and 85.325 has three decimal places.
Like and unlike decimals : Decimals having the same number of decimals places are called like decimals, otherwise they are known as unlike decimals.
For example :
5.25, 15.04, 273.89 are like decimals and 9.5, 18.235, 20.0254 etc. are unlike decimals.
NOTE
We have 0.1 = 0.10 = 0.100 etc, 0.5 = 0.50 etc. and so on. That is by annexing zeros on the right side of the extreme right digit of the decimal part of a number does not alter the value of the number.
Unlike decimals may be converted into like decimals by annexing the requisite number of zeros on the right side of the extreme right digit in the decimal part.
DIVISION OF A UNIT IN TEN EQUAL PARTS
If an object is divided into 10 equal parts then its each part is one tenth of the whole. It is written as 1/10. 1/10 is also written as 0.1 and is read as 'one tenth' or 'decimal one or point one'. thus 1 ones = 10 tenth Ex. 0.5 is read as 5 tenth.
REPRESENTATION DECIMALS ON NUMBER LINE
We have learnt the representation of whole numbers and fractions on a number line. Now we shall explain the method of representing decimal numbers on number line
Let us represent 1.3 on a number line
1.3 is more than 1 and less than 2
1.3 is 1 + 0.3, i.e 1 + 3 tenths
Draw a number line and mark whole numbers 0,1 ,2,3, ....... on it.
Divide the portion between 1 and 2 into 10 equal parts and take 3 parts for 3 tenths or 0.3 Mark it as P. In the above figure P presents the number 1.3.
Ex. Mark the following decimals in place value table :
(a) 0.3 (b) 19.4 (c) 205.9
Sol. Place Value Table
Ex. Write the following in decimal fractions :
(a) 0.8 (b) 1.3
Sol. (a) 0.8 = 8 tenths = 8/10
(b) 1.3 = 1 + 3 tenths = 1 + 3/10
Ex. Write the following as fractions. Reduce them to lowest terms :
(a) 1.0 (b) 3.8
(c) 21.2
Sol. (a) 1.0 = 1
(b) 3.8 = 3 8/10
(c) 21.2 = 212/10 = 21
DIVISION OF A UNIT IN HUNDRED EQUAL PARTS
If an object is divided into 100 equal parts then its each part is one hundredth of the whole. It is written as 1/100.1/100 is also written as 0.01 and is read as 'one hundredth' or 'decimal zero one' or zero point zero one'.
DIVISION OF A UNIT IN THOUSAND EQUAL PARTS
If an object is divided into 1000 equal parts then its each part is one thousandth of the whole. It is written as 1/1000.
1/1000 is also written as 0.001 and is read as 'one thousandth' or decimal zero one' or zero point zero zero one'.
Ex. Write the following decimals in words :
(a) 0.03 (b) 17.38
(c) 10.07 (d) 5.008
Sol. (a) Zero point zero three
(b) Seventeen point three eight
(c) Ten point zero seven
(d) Five point zero zero eight
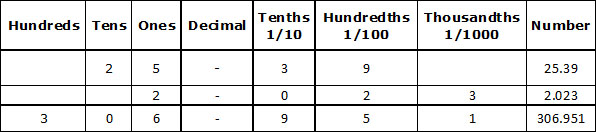
Ex. Place values of digits of numbers are given below.
Write them in decimal form :
(a) 3 tenths, 5 ones, 2 tens, 9 hundredths
(b) 2 hundredths, 3 thousandths, 2 ones
(c) 6 ones, 3 hundreds, 9 tenths, 5 hundredths, 1 thousandth
Sol.
Ex. Write as fraction in lowest terms :
(a) 17.05 (b) 6.32 (c) 45.25
Sol. (a) 17.05 = 17 5/100= 171/20
(b) 6.32 = 632/100 = 6 8/25
(c) 45.25 = 4525/100
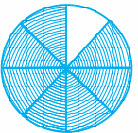
EXPANDED NOTATION FOR DECIMAL NUMERS
Let us study the following examples :
(a) 14.5
= 10 + 4 + 5/10= 10 + 4 + 0.5
(b) 49.08
= 40 + 9 +0/10 +8/10 = 40 + 9 + 0.08
in the above example 14.5 & 49.08 have been written in the expanded form
Ex. Write in the expanded form :
(a) 35.63 (b) 5.003
Sol. (a) 35.63
30 + 5 + 6/10 +3/100 = 30 + 5 + 0.6 + 0.03
(b) 5.003
5 + 0/100 +0/100+3/1000 = 5 + 0.003
Ex. Write in decimal :
(a) 200 + 30 + 5 +7/100 (b) 6 +7/10 +5/100
Sol. (a) 235.07 (b) 6.75
COMPATISON OF DECIMALS
Decimal numbers may be compared by using the following steps :
Step I Obtain the decimal numbers.
Step II Compare the whole number parts of the numbers. The number with greater whole number part will be greater. If the whole number parts are equal, go to next step.
Setp III Compare the extreme left digit of the decimal parts of two numbers. The number with greater extreme left digit will be greater. If the extreme left digits of decimal parts are equal, then compare the next digits and so on.
Ex. Which is greater of 48.23 and 39.35?
Sol. The given decimals have distinct whole number parts, so we compare whole number parts only.
In 48.23, the whole number parts is 48.
In 39.35, the whole number part is 39.
48 > 39
48.23 > 39.35
Ex. Which is greater of 69.7 and 69.68?
Sol. The given decimals have same whole number parts.
so we will compare the decimal parts.
In 69.7 decimal parts is 0.7
In 69.68 decimal part is 0.068
Extreme left digit of 0.7 is 7 and that of 0.68 is 6.
69.7 > 69.68
Ex. Write the following decimals in ascending order :
5.64, 2.54, 3.05, 0.259 and 8.32
Sol. Converting the given decimals into like decimals, we get:
5.640, 2.540, 3.050, 0.259 and 8.320
Ciearly, 0.259 < 2.540 < 3.050 < 5.640 < 8.320
Hence, the given decimals in the ascending order are 0.259, 2.54, 3.05, 5.64 and 8.32
OPERATIONS ON DECIMAL
Addition and Subtraction of Decimals : Decimals can be added or subtracted by using the following steps:
Step - I Convert the given decimals to like decimals.
Step - II Write the decimals in columns with their decimal points directly below each other so that tenths come under tenths, hundredths come under hundredths and so on.
Step -III Add or subtract as we add or subtract whole numbers.
Step -IV Place the decimal point, in the answer, directly below the other decimal points.
Ex. Add 15.44, 7.524 and 25.
Sol. Converting the given decimals to like decimals, we have 15.440, 7.524 and 25.000.
Now,15.440+7.524+25.000=47.964
Ex. Aakash bought vegetables weighing 10 kg. Out of this 3 kg 500 g is onion, 2 kg 75 g is tomab and the rest is potato. What is the weight of potato?
Sol. We have,
Weight of onion = 3 kg 500 g = 3.500 kg
Weight of tomato = 2 kg 75 g = 2.075 kg
Total weight of onion and tomato is :3500kg+2.075kg=5.575kg
Total weight of vegetables = 10 kg
Weight of potato = 10 kg – 5.575 kg = 4.425 kg
Ex. Amit bought a Maths book for Rs. 45.60 and a geometry box for Rs. 62.55 What is the total amount spent by Amit?
Sol. Money spent on Maths book = Rs. 45.60
Money spent on Geometry box = Rs. 62.55
Total amount spent
= Rs. 45.60 + Rs. 62.55
= Rs. 108.15
Ex. Priya travelled 8 km 95 min the first hour, 6 km 298m in the second hour and 7 km 9m in the third hour. Find the total distance travelled by her in three hours.
Sol. Distance travelled in first hour = 8 km 95 m = 8.095 km
Distance travelled in second hour = 6km 298 m = 6.298 km
Distance travelled in third hour = 7 km 9 m = 7.009 km
Total distance travelled in 3 hours
= 8.095 km + 6.298 km+ 7.009 km
= 21.402 km
Ex. An empty box weight 1 kg 240 g. When filled with oranges it weights 19 kg 70 g. What is the weight of the oranges?
Sol. Weight of empty box = 1 kg 240 g
= 1.240 kg
Weight of box with oranges
= 19 kg70 g = 19.070 kg
Weight of oranges
= 19.070 kg – 1.240 kg
= 17.830 kg.
Ex. A can can hold 12.5 litres of mixed fruit juice. 4.035 litres of apple juice and 6 litres 15 ml of orange juice have been poured in the can. What would be the amount of grape juice that can still be added in the can?
Sol. Amount of apple juice = 4.035 L
Amount of orange juice = 6 litres 15 mL = 6.015 L
Capacity of can = 12.5 L
Reqd. amount of grape juice
= 12.5 L – (4.035 + 6.015) L
= 12.5 L – 10.050 L
= 2.45 L
Ex. Subtract the difference of 15.13 and 9.7 from their sum.
Sol. Sum = 15.13 + 9.7 = 24.83
Difference = 15.13 – 9.7 = 5.43
Sum – Difference = 24.83 – 5.43
= 19.40
Ex. Sundaram bought a toothpaste for Rs. 18.75, soap for Rs. 6 and shoe polish for Rs. 12.50 . He gave a fifty rupees note to the shopkeeper. Find the money he got back.
Sol. Cost of the toothpaste = Rs. 18.75
cost of the soap = Rs. 6.00
Cost of the shoe polish = + Rs. 12.50
Total expenditure = Rs. 37.25
Money he got back = Rs. 50 – Rs. 37.25
Rs. 50.00
Rs. 37.25
= Rs. 12.75
Ex. The height of Som is 1.25 m and that of Reena is 1.3 m. Who is taller and by how much?
Sol. Difference in height
= 1.30 m – 1.25 m
= 0.05 m
Thus, Reena is taller by 0.05 m i.e., 5 cm then Som.
Multiplication of Decimals by 10, 100, 1000 etc.:
In order to multiply a decimal by 10, 100, 1000 etc., we use the following rules :
Rule I On multiplying a decimal by 10, the decimal point is shifted to the right by one place.
Rule II On multiplying a decimal by 100, the decimal point is shifted to the right by two places.
Rule III On multiplying a decimal by 1000, the decimal point is shifted to the right by three places and so on.
Ex. Find the following products :
(i) 27.05 × 10 (ii) 429.7 × 100
Sol. We have,
(i) 27.05 × 10 = 270.5 [Shifting the decimal point by one place to the right]
(ii) 429.7 × 100 = 429.70 × 100
= 42970
[Shifting the decimal point by two places to the right]
Multiplication of a decimal by a whole number :
A decimal can be multiplied by a whole number by using the following steps :
Step I Multiply the decimal without the decimal point by the given whole number.
Step II Mark the decimal point in the product to have as many places of decimal as there are in the given decimal.
Ex. Find the product of 0.0275 × 17.
Sol. We have,
275 × 17 = 4675
0.0275 × 17 = 0.4675
Multiplication of a decimal by another decimal :
To multiply a decimal by another decimal, we follow following steps :
Step I Multiply the two decimals without decimal point just like whole numbers.
Step II Insert the decimal point in the product by counting as many places from the right to left as the sum of the number of decimal places of the given decimals.
Ex. Find the product of 9.2 and 6.07.
Sol. We have
,
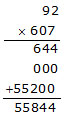
92 × 607 = 55844
Since the sum of the decimal places in the given decimals is 1 + 2 = 3.
So, the product must contain 3 places of decimals.
Hence 9.2 × 6.07 = 55.844
Ex. Multiply 0.0345 by 0.0237
Sol. We have,
345 × 237 = 81765
We observe that the sum of the decimals in the given decimals is 4 + 4 = 8
So, the product must contain 8 places of decimals
Hence, 0.0345 × 0.0237 = 0.00081765
Dividing a decimal by 10, 100, 1000 etc.:
A decimal, can be divided by 10, 100, 1000 etc. by using the following rules :
Rule I When a decimal is divided by 10, the decimal point is shifted to the left by one place.
Rule II When a decimal is divided by 100, the decimal point is shifted to the left by two places.
Rule III When a decimal is divided by 1000, the decimal point is shifted to the left by three places.
Ex. Divide
(i) 12.75 by 10 (ii) 1275.7 by 1000
Sol. (i) 12.75÷ 10 =12.75/10 = 1.275
[Shifting decimal point to the left by 1 place]
(ii) 1275.7÷ 1000 =1275.7/1000 = 1.2757
[Shifting decimal point to the left by 3 place]
DIVIDING A DECIMAL BY A WHOLE NUMBER
A decimal can be divided by a whole number by using the following steps :
Step I Check the whole number part of the dividend.
Step II If the whole number part of the dividend is less then the divisor, then place a '0' in the ones place in the quotient, other wise, go to step III.
Step III Divide the whole number part of the dividend.
Step IV Place the decimal point to the right of ones place in the quotient obtained in step I.
Step V Divide the decimal part of the dividend by the divisor. If the digits of the dividend are exhausted, then place zeros to the right of dividend and remainder each time and continue the process.
Ex. Divide 93.45 by 15
Sol. We have,
93.45÷ 15 = 6.23
EXAMPLE. Divide 0.6204 by 5
Sol. We have
,
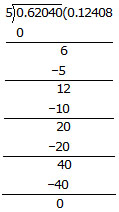
Thus, 0.6204÷ 5 = 0.12408.
Dividing a decimal by a decimal : A decimal can be divided by a decimal by using the following steps :
Step I Multiply the dividend and divisor by 10 or 100 or 1000 etc. to convent the divisor into a whole number.
Step II Divide the new dividend by the whole number obtained in step I.
Ex. Divide 0.00942 by 0.314
Sol. We have,
0.00942/0.314=9.42/314
Hence, 0.00942 ÷ 0.314 = 0.03
Ex. Divide 0.0024 by 0.04
Sol. We have,
0.0024/0.04=0.24/4
Hence, 0.0024÷ 0.04 = 0.06.
Ex. The cost of 28 toys of the same kind is Rs 3462.20.
Find the cost of each toy.
Sol. Cost of 28 toys = Rs 3462.20.
Cost of 1 toy = Rs (3462.20÷ 28)
= Rs(3462.20/28)
= Rs 123.65
Hence, the cost of each toy is Rs 123.65.
Ex. The product of two decimals is 1.5008. If one of them is 0.56, find the other.
Sol. Product of given decimals = 1.5008.
One decimal = 0.56.
The other decimal = 1.5008÷ 056
=1.5008/0.56
= 2.68
Hence, the other decimal is 2.68
OBJECTIVE TYPE
Q.1 1.04 = ?
(A)11/5 (B)12/5 (C) 11/25 (D) None of these
Q.2 Which of the following is a true statement?
(A) 1.14 > 1.2 (B) 1.143 > 1.15 (C) 1.14 < 1.2 (D) 1.14 < 1.040
Q.3 What should be subtracted from 0.1 to get 0.03 ?
(A) 0.7 (B) .07 (C) .007 (D) None of these
Q.4 What should be added to 3.07 to get 3.5 ?
(A) 0.57 (B) 0.34 (C) 0.43 (D) 0.02
Q.5 0.4 × 0.4 × 0.4 = ?
(A) 6.4 (B) 0.64 (C) 0.064 (D) None of these
Q.6 2.08÷ (0.16) = ?
(A) 13 (B) 0.13 (C) 1.3 (D) None of these
Q.7 Express, 5kg 8g as kg using decimal :
(A) 5.8 kg (B) 5.08 kg (C) 5.008 kg (D) 58 kg
Q.8 The product of two decimals is 1.8576. If one of the decimals is 0.54, find the other.
(A) 3.44 (B) 34.4 (C) .344 (D) 344
Q.9 Find the weight of 16 bags of sugar, each weighing 48.450 kg.
(A) 77.520 kg (B) 7.7520 kg (C) 7752 kg (D) 775.20 kg
Q.10 A car can cover a distance of 8.6 kg in one litre of petrol. How far can it go on 36.5 litres of petrol ?
(A) 313.9 km (B) 31.39 km (C) 0.3139 km (D) 3139 km
Q.11 0.4 can be written as :
(A)4/10 (B)4/100 (C)4/1000 (D) None of these
Q.12 Decimal number part of 7.25 is
(A) 7 (B) 0.2 (C) 0.25 (D) 0.05
Q.13 How many 1/10 together make 1 ?
(A) 10 (B) 1 (C) 100 (D) none of these
Q.14 Decimal representation of 7+4/10+3/100 is :
(A) 0.743 (B) 7.43 (C) 74.3 (D) 0.43
Q.15 How many km are there in 1 m ?
(A) 0.1 (B) 0.01 (C) 0.001 (D) 0.0001
Q.16 The weight of Jaya, Sabina, Sanju and Rohit are 1.16 m, 162 cm, 1600 mm and 1640 mm respectively.
Who is the tallest of them all ?
(A) Jaya (B) Sabina (C) Sanju (D) Rohit
Q.17 The weight of a basket ball is about 600000 mg. It is :
(A) less than 600 g (B) greater than 600 g
(C) equal to 600 g (D) none of these
Q.18 Which decimal number is greater than ?
(A) 0.5 (B) 0.85 (C) 0.73 (D) 0.75
Q.19 0.99, 9.90, 9.09, 0.90, 0.909 arranged in descending order are :
(A) 9.09, 0.99, 9.90, 0.90, 0.909
(B) 9.90, 9.09, 0.99, 0.909, 0.90
(C) 9.90, 0.99, 0.909, 9.09, 0.90
(D) 9.09, 9.90, 0.99, 0.909, 0.90
Q.20 When 0.02 is written as a fraction in the simplest form, the sum of the numerator and denominator is :
(A) 12 (B) 21 (C) 51 (D) 100
SUBJECTIVE TYPE
Q.1 Write the following decimals in the place value table :
(i) 23.506 (ii) 5.678
Q.2 Write each of the following as decimals :
(i) two hundred and seven hundredths
(ii) three tens five ones seven tenth and two hundredth
Q.3 Show the following number on number line
(i) 1.7 (ii) 2.3
Q.4 Write the following decimal as fraction. Reduce the fraction to lowest form
(i) 3.5 (ii) 80.25
Q.5 Write as decimals
(i) 3/5 (ii)7/4
Q.6 Write each of the following as decimal.
(i) 300 + 50 + 7 +5/10 +9/100
(ii) 300 +3/100 + 8/1000
Q.7 Write the following decimal in words
(i) 23.57 (ii) 4.06
Q.8 Which one is greater
(i) 5.678, 5.67 (ii) 2.3, 2.257
Q.9 Using decimal express
(i) 27 rupees and 3 paise as rupees
(ii) 5 cm as meter
(iii) 9 cm 8 mm as cm
(iv) 26 kg 30 g as kg
Q.10 Find the cost of one pen if the cost of 24 pens is Rs. 2986.80
Q.11 A bowler took 15 wickets for 321 runs. What is his average score per wicket?
Q.12 Mr. Soni bought some bags of cement, each weighing 49.8 kg. If the total weight of all the bags is 1792.8 kg, how many bags did he buy ?
Q.13 Add (Frist express metric measures in decimal notation and then odd.)
(i) Rs. 107.69 + Rs. 596.84
(ii) 13 km 831 m and 5 km 78 m
(iii) 17 g 8 mg, 295 g 87 mg, 64 g 392 mg
Q.14 Subtract : (First express metric measure in decimal notation)
(i) 7 km 698 m from 15 km 25 m
(ii) 25 m 89 cm from 40 m 2 cm
(iii) 12 L 45 mL from 15 L 600 mL
Q.15 What must be added to 89.191 to get the smallest 3-digit number?
Q.16 The sum of three numbers is 112.165. If two numbers are 25.5 and 59.63, find the third number.
Q.17 Shalini spent Rs. 835.75 on buying clothes, Rs. 309.15 on buying fruits and vegetables, Rs. 168.90 on buying sweets and Rs. 60.50 on transport. She had 3 five hundred rupee notes in her purse. How much money was left with her ?
Q.18 Mani was 1.35 m tall in 2004. His height increase 0.2 m in one year. What is his height in 2005?
Q.19 Convent each of the following decimals into a fraction in the lowest terms :
(i) 0.325 (ii) 0.075 (iii) 0.550 (iv) 0.005
Q.20 Arrange in the increasing order :
(i) 0.125, 0.521, 0.152, 1.215
(ii) 4.123, 4.132, 41.320, 14.203
Fractions and Decimals
In questions 1 to 20, out of the four options, only one answer is correct. Choose the correct answer.
1. The fraction which is not equal to 4/5 is
(A) 40/50 (B) 12/15 (C) 16/20 (D) 9/15
2. The two consecutive integers between which the fraction 5/7 lies are
(A) 5 and 6 (B) 0 and 1 (C) 5 and 7 (D) 6 and 7
3. When 1/4 is written with denominator as 12, its numerator is
(A) 3 (B) 8 (C) 24 (D) 12
4. Which of the following is not in the lowest form?
(A) 7/5 (B) 15/20 (C) 13/33 (D) 27/28
5. If 5/8=20/P , then value of p is
(A) 23 (B) 2 (C) 32 (D) 16
6. Which of the following is not equal to the others?
(A) 6/8 (B) 12/16 (C) 15/25 (D) 18/24
7. Which of the following fractions is the greatest?
(A) 5/7 (B) 5/6 (C) 5/9 (D) 5/8
8. Which of the following fractions is the smallest?
(A) 7/8 (B) 9/8 (C) 3/8 (D) 5/8
9. Sum of 4/17 and 15/17 is
(A) 19/17 (B) 11/17 (C) 19/34 (D) 2/17
10. On subtracting 5/9 and 19/9 the result is
(A) 24/9 (B) 14/9 (C) 14/18 (D) 14/9
11. 0.7499 lies between
(A) 0.7 and 0.74 (B) 0.75 and 0.79 (C) 0.749 and 0.75 (D) 0.74992 and 0.75
12. 0. 023 lies between
(A) 0.2 and 0.3 (B) 0.02 and 0.03 (C) 0.03 and 0.029 (D) 0.026 and 0.024
13. 11/7 can be expressed in the form
(A) 71/4 (B)41/4 (C)1/4/7 (D) 111/7
14. The mixed fraction can be expressed as
(A) 33/7 (B) 39/7 (C) 33/4 (D) 39/4
15. 0.07 + 0.008 is equal to
(A) 0.15 (B) 0.015 (C) 0.078 (D) 0.78
16. Which of the following decimals is the greatest?
(A) 0.182 (B) 0.0925 (C) 0.29 (D) 0.038
17. Which of the following decimals is the smallest?
(A) 0.27 (B) 1.5 (C) 0.082 (D) 0.103
18. 13.572 correct to the tenths place is
(A) 10 (B) 13.57 (C) 14.5 (D) 13.6
19. 15.8 – 6.73 is equal to
(A) 8.07 (B) 9.07 (C) 9.13 (D) 9.25
20. The decimal 0.238 is equal to the fraction
(A) 119/500 (B) 238/25 (C) 119 / 25 (D) 119 / 50
In questions 21 to 44, fill in the blanks to make the statements true:
21. A number representing a part of a _________ is called a fraction.
22. A fraction with denominator greater than the numerator is called a_________ fraction.
23. Fractions with the same denominator are called _________ fractions.
24. 135/18is a _________ fraction.
25. 18/5 is an ______ fraction.
26. 7/19 is a ______ fraction.
27. 5/8 and 3/8 are ______ proper fractions.
28. 6/11 and 6/13 are ______ proper fractions.
29. The fraction 6/15in simplest form is ______.
30. The fraction 17/34in simplest form is ______.
31. 18/135 and 90/675are proper, unlike and ______ fractions.
32. 82/7is equal to the improper fraction ______.
33. 87/7 is equal to the mixed fraction ______.
34. 9+2/10+6/100 is equal to the decimal number ______.
35. Decimal 16.25 is equal to the fraction ______.
36. Fraction 7/25 is equal to the decimal number ______.
37.17/9+41/9
38 67/14-24/14
39.17/2+31/2=
40.91/4-5/4
41. 4.55 + 9.73 = ______.
42. 8.76 – 2.68 = ______.
43. The value of 50 coins of 50 paisa = Rs ______.
44. 3 Hundredths + 3 tenths = ______.
In each of the questions 45 to 65, state whether the statement is true or false:
45. Fractions with same numerator are called like fractions.
46. Fraction 18/39 is in its lowest form.
47. Fractions 15/39 and 45/117 are equivalent fractions.
48. The sum of two fractions is always a fraction.
49. The result obtained by subtracting a fraction from another fraction is necessarily a fraction.
50. If a whole or an object is divided into a number of equal parts, then each part represents a fraction.
51. The place value of a digit at the tenths place is 10 times the same digit at the ones place.
52. The place value of a digit at the hundredths place is 1/10 times the same digit at the tenths place.
53. The decimal 3.725 is equal to 3.72 correct to two decimal places.
54. In the decimal form, fraction 25/8=3.125
55. The decimal 23.2=232/5
56. The fraction represented by the shaded portion in the adjoining figure is 3/8

57. The fraction represented by the unshaded portion in the adjoining figure is 5/9

58.25/19+6/19=31/38
59.8/18-8/15=8/3
60.7/12+11/12=3/2
61. 3.03 + 0.016 =3.019
62. 42.28 – 3.19 = 39.09
63.16/25 >13/25
64. 19.25 < 19.053 65. 13.730 = 13.73
In each of the questions 66 to 71, fill in the blanks using ‘>’, ‘<’ or ‘=’ :
66. 11/16 ....14/15
67. 8/15 .......95/14
68. 12/75 ........32/200 69. 3.25... 3.4
70.18/15........1.3
71. 6.25..........25/4
72. Write the fraction represented by the shaded portion of the adjoining figure:
73. Write the fraction represented by the unshaded portion of the adjoining figure:
74. Ali divided one fruit cake equally among six persons. What part of the cake he gave to each person?
75. Arrange 12.142, 12.124, 12.104, 12.401 and 12.214 in ascending order.
76. Write the largest four digit decimal number less than1using the digits 1, 5, 3 and 8 once.
77. Using the digits 2, 4, 5 and 3 once, write the smallest four digit decimal number.
78. Express 11/20 as a decimal.
79. Express 62/3 as an improper fraction.
80. Express 32/5 as a decimal.
81. Express 0.041 as a fraction.
82. Express 6.03 as a mixed fraction.
83. Convert 5201g to kg.
84. Convert 2009 paise to rupees and express the result as a mixed fraction.
85. Convert 1537cm to m and express the result as an improper fraction.
86. Convert 2435m to km and express the result as mixed fraction.
87. Arrange the fractions 2/3,3/4,1/2 and 5/6 in ascending order.
88. Arrange the fractions and 6/7,7/8,4/5,3/4
89. Write 3/4 as a fraction with denominator 44.
90. Write 5/6 as a fraction with numerator 60.
91. Write 129/8 as a mixed fraction.
92. Round off 20.83 to nearest tenths.
93. Round off 75.195 to nearest hundredths.
94. Round off 27.981 to nearest tenths.
95. Add the fractions 3/8 and 2/3.
96. Add the fractions 3/8 and .63/4
97. Subtract 1/6 and 1/2 .
98. Subtract 81/3 and .100/9
99. Subtractand 11/4 and 61/2
100. Add 11/4 and .61/2
ANSWER KEY -1
OBJECTIVE :
1. C 2. C 3. B 4. C 5. C 6. A 7. C 8. A 9. D 10. A
11. A 12. C 13. A 14. B 15. C 16. D 17. C 18. B 19. B 20. C
SUBJECTIVE :
1.

2. (i) 200.07 (ii) 35.72
3.

Point P Represent 1.7 and Point Q represent 2.3.
4. (i) 7/2 (ii)321/4
5. (i) 0.6 (ii) 1.75
6. (i) 357.59 (ii) 300.038
7. (i) two tens, three ones, five tenth and seven hundredth
(ii) Four ones and six hundredth
8. (i) 5.678 > 5.67 (ii) 2.3 > 2.257
9. (i) 27.03Rs. (ii) 0.05m (iii) 9.8cm (iv) 26.030 Kg
10. Rs.124.45 11. 21.4 runs per wicket 12. 36
13. (i) Rs.704.53 (ii) 18.909 (iii) 376.487
14. (i) 7.327 km (ii) 14.13m (iii) 3.555L
15. 10.809 16. 27.035 17. Rs.125.70 18. 1.55m
19. (i)13/40 (ii)3/40 (iii)11/20 (iv)1/200
20. (i) 0.125, 0.152, 0.521, 1.215 (ii) 4.123, 4.132, 14.203, 41.320
ANSWER KEY -2
1. D 2. B 3. A 4. B 5. C 6. C 7. B 8. C 9. A 10. B
11. C 12. B 13. C 14. B 15. C 16. C 17. C 18. D 19. B 20. A