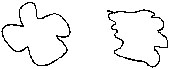PERIMETER
The perimeter of a closed figure is the length of the boundary of the figure.
we find perimeter when we
(a) walk around a garden.
(b) want to know the cost of fencing the fleid.
(c) build a boundary wall around our house.
(d) put a lace around a table cover.
(e) want to know the wood stick required to make a picture frame.
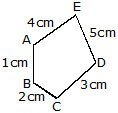
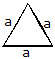
The perimeter of this pentagon is sum of the sides
AB + BC + CD + DE + EA = 1cm + 2cm + 3cm + 5cm + 4cm = 15cm
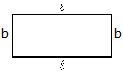
Perimeter of Rectangle:
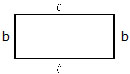
The perimeter of a rectangle is the sum of all its sides.
The opposite sides of rectangle are equal. If one side, say the longer side, is l unit and the shorter side is b unit, then perimeter = twice the length + twice the breadth.
Perimeter = length + breadth + length + breadth = 2(length) + 2(breadth) = 2(length + breadth)
= 2(l + b) where l = length
b = breadth
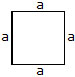
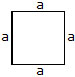
Perimeter of a square :
A square is a special rectangle with all the four sides equal. If one side of a square measures a unit, we can say that both the length and the breadth are a unit each.
Perimeter of a square = 2(l + b)
= 2(a + b)
= 2 × 2a
= 4a
= 4 times the side
The perimeter of a square is equal to four times the length of its sides.
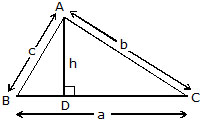
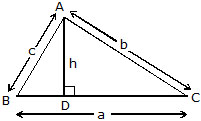
Perimeter of a triangle :
perimeter = a + b + c
Perimeter of an equiliateral triangle :
A triangle with all sides equal is called an equilateral triangle. If the length of one side of an equilateral triangle is a units, its perimeter will be side + side + side = a + a + a + 3a
In general, if the sides of a polygon are equal, that is, if it is a regular polygon, its perimeter will be the product of the length of its side with the number of sides.
Perimeter of a regular pentagon = 5a units
Perimeter of a regular hexagon = 6a units
Perimeter of a regular octagon = 8a units
where a is the length of one side.
Ex. Find the perimeter of rectangle having length 12cm and breadth 8cm.
Sol. Length = 12cm
Breadth = 8cm
Perimeter of rectangle= 2(length + breadth)
= 2(12 + 8)
= 40cm
Ex. Find the side of square having perimeter 28 cm
Sol. Perimeter of square = 4 × side
Side =Perimeter/4=28/4 = 7cm
Ex. Find the cost of fencing a square park of side 300 m at the rate Rs. 25 per meter
Sol. Perimeter of square = 4 × side
= 4 × 300 = 1200 m
Cost of fencing = Perimeter x cost per meter
1200 × Rs. 25
= Rs. 30,000
Ex. A rectangular field is 90 m by 70 m. A man walks round it at the rate 4 km per hour. What time will he take in making 5 rounds ?
Sol. Distance covered in one round
= Perimeter of the field
= 2(90 + 70) m = 2 × 160m = 320m
Distance covered in 5 rounds
= 320m × 5 = 1600 m
The man walks 4 km = 4 × 1000 m in one hr.
The men walks 1600 m in
1/4000× 1600 hour = hour
= 2/5 × 60 minutes = 24 minutes
Ex. Mr. Verma has an orchard of length and breadth 280 m and 200 m respectively. He wants to fence it with 4 rounds of barbed wire. Find the cost of fencing at Rs. 35 per meter.
Sol. Length of orchard = 280 m
Breadth of the orchard = 200
= 2(280m + 200 m)
= 2 × 480 = 960 m
length of barbed wire required for 4 rounds of fencing = 4 × 960 m = 3840 m
Cost of fencing at Rs. 35 per metre
= Rs. (3840 × 35) = Rs. 1,34,400
Ex. A piece of string is 48 cm long. What will be the length of each side if the string is used to form :
(i) a square
(ii) an equilateral triangle
(iii) an regular octagon
Sol. (i) one side of the square
Perimeter ÷ 4 = 48 ÷ 4 = 12 cm
(ii) one side of the equilateral triangle
= Perimeter ÷ 3 = 48 ÷ 3 = 16 cm
(iii) one side of regular octagon
= Perimeter ÷ 8 = 48 ÷ 8 = 6 cm
AREA
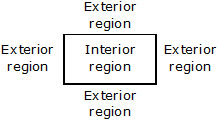
The amount of surface of the plane covered by a closed figure is called its area.
For every closed figure, there are two regions.
The term 'area' refers to the measure of the total interior region.
we find area when we
(a) Level the ground
(b) Paint the wall
(c) Cover the floor with the tiles
No. of tiles = Area of floor/Area of tiles
Look at the closed figures given below. All of them occupy some region. can you tell which one occupies more region? It is difficult to make out unless we meaure the area.
In order to calculate which closed figure having larger area we place them on a squared paper or graph paper where every square measures 1 cm × 1 cm.
Make an outline of the figure.
Look at the square enclosed by the figure. Some of them are completely enclosed some half, some less than half and some more than half.
The area is the number of centimeter squares that are needed to cover it.
But there is a small problem that the square do not always fit exactly into the area you measure.
We get over this difficulty by adopting a convention.
The area of one full square is taken as 1 sq unit. if it is a centimetre square sheet, then area of one full area will be 1 sq. cm.
lgnore portions of the area that are less than half a square.
If more than half of a square is in a region, just count it as one square.
If exactly half the square is counted, take its area as sq unit.
Such a convention given a fair estimate of the desired area.
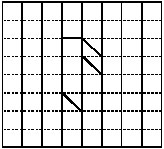
Ex. Find the area of the shape shown in the figure.
Sol. This figure is made up of line segments moreover, it is covered by full squares and half squares only. This makes our job simple.
(i) fully filled square = 3
(ii) half filled square = 3
Area covered by full squares
= 3 × 1 sq units = 3 sq units
Area covered by half squares
= 3 × 1/2 sq units = 11/2 sq units
Total area = 3 + 11/2 = 41/2 sq units.
Area of rectangle : For rectangle having length l unit and breadth b units.
Area of rectangle = l × b sq. unit
Area of square : For square having side a unit.
Area of square = a × a sq. unit
Area of a triangle :
Area =1/2 × Base × Height =1/2 ah
Ex. Find the area of a square whose side is 10 m.
Sol. Side of the square = 10m
Area of the square = side × side
= (10 × 10) sq m
= 100 sq m
Ex. Find the breadth of a park whose area is 1500 sq. m and length is 50m
Sol. Area of the park = 1500 sq m
Length of the park = 50 m
Breadth of the park =
= (1500 ÷ 50)m = 30 m
Ex. Find the side of a square whose area is 25 sq. m.
Sol. Now we find the number which when multiplied by itself gives us 25.
clearly, this number is 5.
side of the square = 5m.
Ex. A rectangle and a square are equal in area. The side of the square is 24 m. Find the width of the rectangle if it is 36m long. Are their perimeters equal ?
Sol. Side of the square = 24 m
Area of the square = 24 × 24 sq m = 576 sq m
Area of the rectangle = area of the square
= 576 sq m
Length of the rectangle = 36 m
Breadth of the rectangle = m 576/36= 16 m
Perimeter of the square = 4 × 24 m = 96 m
Perimeter of the rectangle = 2(length + breadth)
= 2 (36 m + 16 m) = 2 × 52 m = 104 m
Their perimeters are not equal.
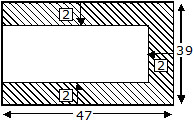
Ex. In given figure, find the area of the shaded portion when all dimensions are given in centimeters.
Sol. Length of the bigger rectangle = 47 cm
Breadth of the bigger rectangle = 39 cm
Area of the bigger rectangle = length × breadth
= (47 × 39) sq cm = 1833 sq cm
Length of the smaller rectangle = (47 – 2)cm = 45cm
Breadth of the smaller rectangle = (39 – 2 – 2)cm = 35cm
Area of the smaller rectangle = (45 × 35)sq cm
= 1575 sq cm
Area of shaded portion = (1833 – 1575) sq cm
= 258 sq cm
Ex. Find the cost of levelling a playground at Rs. 3 per square metre if it is 30 m long and 15 m wide.
Find also the cost of fencing it at Rs. 1.20 per metre.
Sol. Length of the playground = 30 m
Breadth of the playground = 15 m
Area of the playground = 30 × 15 sq m = 450 sq m
Cost of levelling 1 sq m = Rs. 3
Cost of levelling 450 sq m = Rs. 450 × 3 = Rs 1350
Perimeter of the playground = 2 (length + breadth)
= 2(30 + 15)m = 90 m
Cost of fencing 1 m = Rs. 1.20
Cost of fencing 90 m = Rs. 1.20 × 90 = Rs. 108
Ex. How many square tiles of side 18 cm will be required to pave the floor of a rectangular room 5.4 m × 4.8 m?
Sol. Length of the floor = 5.4 m = 540 cm
Breadth of the floor = 4.8 m = 480 cm
Area of the floor = 540 × 480 sq cm
= 259200 sq cm
Area of one tile = 18 × 18 sq cm = 324 sq cm
Number of tiles required = 259200/324= 800
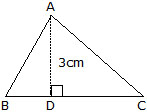
Ex. In given figure, if the area of the triangle ABC is 36 cm2 and the height AB is 3 cm than the base would be
Sol. Given area = 36 sq cm and height = 3cm base = ?
Area of the triangle = (base × height) ÷ 2
36 = (base × 3) ÷ 2
base = (36 × 2) ÷ 3
= 24 cm
SOLID FIGURES
You already know that the geometerical figure which have only two dimensions are called the plane figures. A figure which have three dimensions as length, breadth and height is not a plane figure and we can not draw such figures on black board exactly. These three dimensional figures are called solids for example Cube, cuboid, cylinder cone, sphere etc. are some three dimensional figures. In this section we will leam how we determine the surface area of such solids.
DEFINITIONS
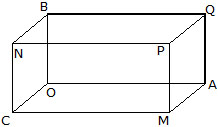
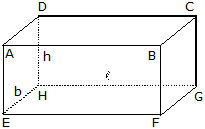
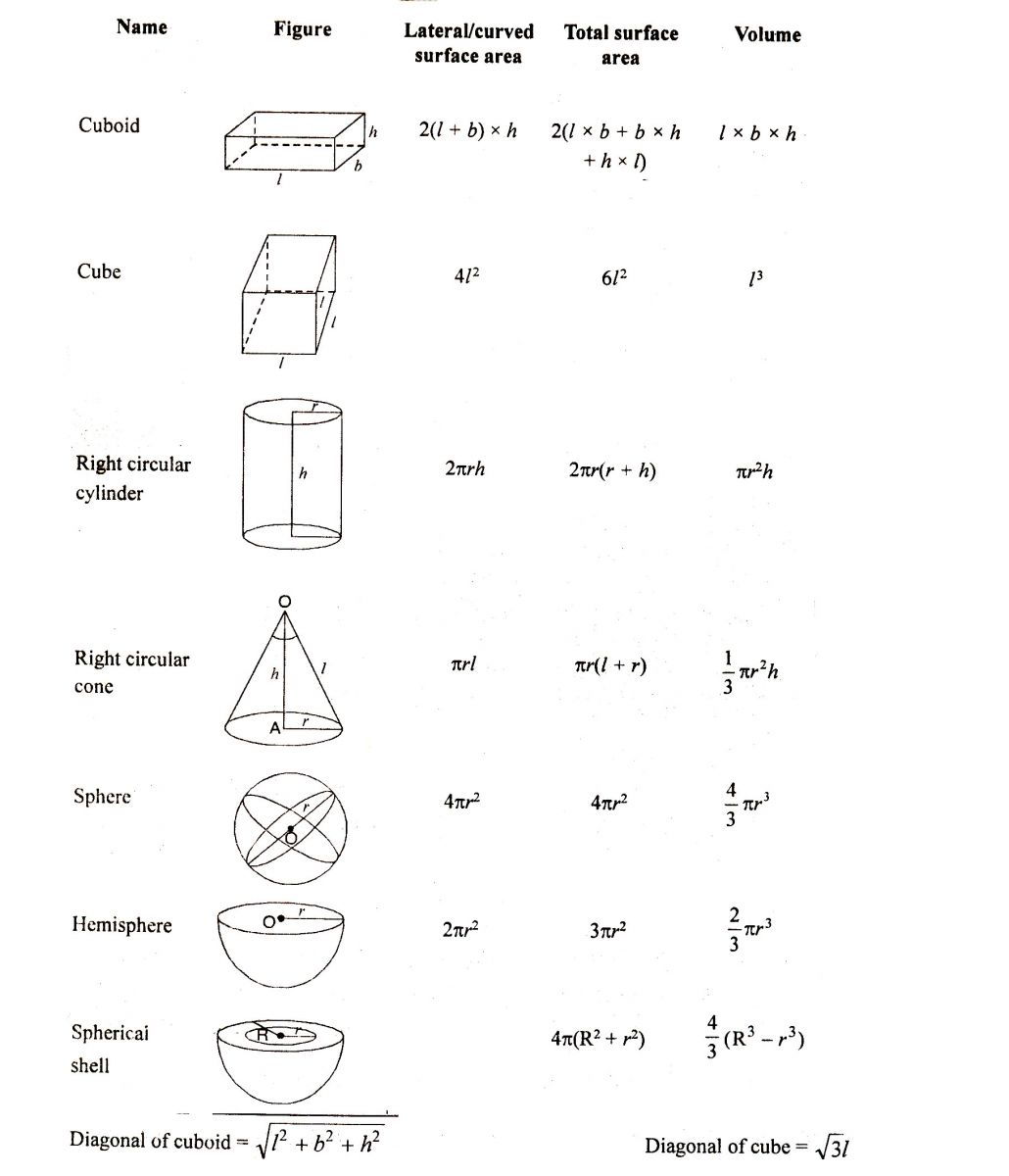
(i) Cuboid : A solid bounded by six rectangular plane regions is called a cuboid. [Figure below]
A cuboid has six faces OAQB, CMPN, OAMC, BQPN, PQAM and OCNB, eight vertices O, P, Q, M, N, A, B and C, twelve edges : OA, BQ, NP, CM, PM, CN, OB, AQ, BN, PQ, MA and OC and four diagonals OP, CQ, BM and AN.
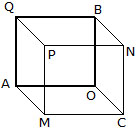
Cube : A cuboid whose length, breadth and height are all equal is called a cube. [Figure below].
SURFACE AREA OF CUBE & CUBOID
(i) Surface area of a cuboid : In earlier section, we have learned about a cuboid and a cube. As we have seen that the surface of a cuboid consists of six rectangular faces. So, the surface area of a cuboid is equal to the sum of the areas of its six rectangular faces. In this section, we shall derive the formula for the surface area of a cuboid.
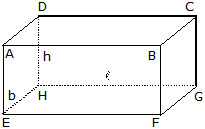
Consider a cuboid whose length is l cm, breadth b cm and height h cm as shown in Figure.
Area of face ABCD = Area of face of face EFGH = (l × b) cm2
Area of face AEHD = Area of face BFGC = (b × h) cm2
Area of face ABFE = Area of face DHGC = (l × h) cm2
Total surface area of the cuboid
= Sum of the areas of all its six faces
= 2 (l × b) + 2 (b × h) + 2(l × h) cm2
= 2 (l × b + b × h + l × h) cm2
= 2 (lb + bh + lh) cm2
= 2 (length × breadth + breadth × height + length × height) cm2
For the calculation of surface area of a cuboid, the length, breadth and height must be expressed in the same units.
(ii) Surface area of a cube : Since all the faces of a cube are squares of the same size i.e. for a cube we have l = b = h. Thus, if l cm is the length of the edge of side of a cube, then
Surface area of the cube = 2(l × l + l × l + l × l)
2 × 3l2 = 6l2 = 2 (Edge)2
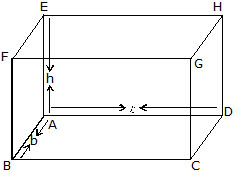
(iii) Lateral surface area of a cuboid and a cube : If out of the six faces of a cuboid, we only find the sum of the areas of four faces leaving the bottom and top faces. This sum is called the lateral surface area of the cuboid. Consider a cuboid of length l, breadth b and height h as shown in figure.
Lateral surface of the cuboid,
= Area of face AEHD + Area of face BFGC + Area of face ABFE + Area of face DHGC
= 2 (b × h) + 2 (l × h)
= 2 (l + b) × h
= 2 (Length + breadth) × Height
= perimeter of the base × Height
Lateral surface area of the cube
= 2 (l × l + l × l)
= 2 (l2 + l2) = 4l2 = 4(Edge)2
Ex. Find the side of a cube whose surface area is 600 cm2.
Sol. Surface area of a cube = 6 (side)2
6 (side)2 = 600
(Side)2 =600/6 = 100 (10)2
Side = 10 cm
Hence, side of the cube = 10 cm.
Ex. If length and breadth of a cuboid is 4 cm and 6 cm and having total surface area is 208 cm2 then find the height of cuboid.
Sol. Let L = 4 cm, B = 6 cm
Total surface area of cuboid = 2(LB + BH + HL)
208 = 2[4 × 6 + 6 × H + H × 4]
208 = 2[24 + 6 × H + H × 4]
208 = 2[24 + 10H]
24 + 10 H = 208/2 = 104
10 H = 104 – 24 = 80
H =80/10 = 8
there for height of the cuboid = 8 cm
VOLUMES OF SOLID FIGURES
Now you are familiar with solid figures and their surface areas. These figure lie in space, i.e., in three dimensions. These figures can not lie entirely on a two dimensional plane. As these figures lie in space so they cover a part of sapce, that part of space is called volume of that solid figure. The volume of a solid is the amount of space enclosed by its bounding surface. The unit of volume is cubic centimeter or cubic meter. The basic formula for volume is area of base × height. In this section we will study how we determine the volume of some solid figures like cube, cuboid, cylinder, cone, sphere etc.
IMPORTANT FORMULAE
Recall that the volume of a soild object is the measure of the space occupied by it. In our day-to-day life we also come across hollow objects. The interior of a hollow object can be filled with air or some liquid that takes the shape of the object. In such cases, the volume of the object can accommondate is called the capacity of the hollow object. Thus, we may say that the volume of an object is the measure of the space it occupies and the capacity of an object is the volume of the substance its interior can accommodate.
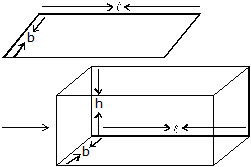
(i) Volume of cuboid : Let there be a cuboid of length l, breadth b and height h as in fig.. The area of the rectangular base ABCD of the cuboid is (l × b).
If we take rectangular sheets congruent to the base ABCD of the cuboid and the sheets are put one over the other as shown in fig.. Then, the height to which the sheets are stacked to form the cuboid is h.
Measure of the space occupied by the cuboid
= Area of a rectangular sheet × h
= (l × b) × h
= lbh
Hence,
Volume of the cuboid = l b h = Length × Breadth × Height
Also, Volume of the cuboid = Area of the base × Height
REMARKS :
(i) While finding the volume of a cuboid, its length, breadth and height must be expressed in the same units.
(ii) From the above formula, we obtain
Length = volume/breadth×height
Breadth =volume/length×height
Height = volume/length×height
(iii) Volume of a cube : We known that a cube is special type of a cuboid whose length, breadth and height are all equal.
So, the volume V of cube edge l is given by
V = l × l × l × l3 = (Edge)3
Ex. Find the number of 8 cm cubes that can be cut out of a cube of side 24 cm.
Sol. Number of cubes =
N =243/83 = 33 = 27
Ex. A cube of 9 cm edge is immersed completely in a rectangular vessel containing water. If the dimensions of the base are 15 cm and 12 cm. Find the rise in water level in the vessel.
Sol. We have
Edge of the given cube = 9 cm.
Volume of the cube = (9)3 cm3 = 729 cm3
If the cube is immersed in the vessel, then the water level rises. Let the rise in water level be h cm.
Clearly,
Volume of the cube = Volume of the water replaced by it.
Volume of the cube
= Volume of a cuboid of dimension 15 cm × 12 cm × h cm
729 = 15 × 12 × h
h = 729/15×12×h cm
h = 81/20 cm = 4.05 cm.
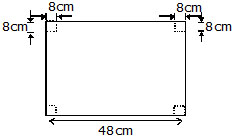
Ex. A metallic sheet is of the rectangular shape with dimenstion 48 cm × 36 cm. From each one of comers, a square of 8 cm is cut off. An open box is made of the remaining sheet. Find the volume of the box.
Sol. In order to make an open box, a square of side 8 cm is cut off from each of the four comers and the flaps are folded up.
Thus, the box will have the following dimensions :
Length = (48 – 8 – 8) cm = 32 cm,
Breadth = (36 – 8 – 8) cm = 20 cm,
Height = 8 cm
Volume of the box formed = (32 × 20 × 8) cm3 = 5120 cm3
SOME IMPORTANT FORMULE
Q.1 The perimeter of regular pentagon of side 8 cm is :
(A) 32 cm (B) 40 cm (C) 48 cm (D) 56 cm
Q.2 Find the area of square having perimeter 20 cm.
(A) 5 cm2 (B) 10 cm2 (C) 20 cm2 (D) 25 cm2
Q.3 A regular polygon having n side perimeter m unit, then length of each side of polygon is :
(A) mn unit (B) – l unit (C) unit (D) can't be determine
Q.4 Rectangle having length l unit and perimeter p unit then its breadth is :
(A) unit (B) unit (C) + l unit (D) unit
Q.5 A rectangular floor having dimension 40m × 30m is paved with square tiles of side 5 m, find the number of tiles required.
(A) 24 (B) 48 (C) 96 (D) 120
Q.6 If the area and length of a rectangular plot are 440 m2 and 22 m respectively, then find its breadth ?
(A) 20 m (B) 10 m (C) 30 m (D) 40 m
Q.7 A lawn is in the shape of a rectangle of length 80 m and width 40 m. Out side the lawn there is footpath of uniform width 3 cm. Find the area of the path.
(A) 756 m2 (B) 706 m2 (C) 736 m2 (D) 726 m2
Q.8 The length and width of a rectangular field are 500 m and 400 m respectively; within it two roads of 10 metres width run parallel to both sides. Find the area covered by both the roads.
(A) 8800 m2 (B) 8900 m2 (C) 8860 m2 (D) 8830 m2
Q.9 The cost of levelling a playground at Rs.5 per square meter is Rs. 7000. It is 20 m wide. Find the cost of fencing it at Rs.2 per meter.
(A) Rs. 330 (B) Rs. 340 (C) Rs. 350 (D) Rs. 360
Q.10 A street lane is to be paved with bricks. The length of the lane is 200 m and its breadth 15m. Find the number of bricks required to pave the lane if each brick measures 20 cm by 10 cm
(A) 15 (B) 150 (C) 1500 (D) 150000
Q.11 The perimeters of two square are 748 cm and 336 cm. Find the perimeter of a square whose area is equal to the sum of the areas of these two squares :
(A) 810 cm (B) 815 cm (C) 820 cm (D) 825 cm
Q.12 The dimensions of a hall are 40 m, 25 m and 20 m. If each person requires 200 cubic metres.
Then the number of persons who can be accommodated in the hall are :
(A) 120 (B) 150 (C) 140 (D) 100
Q.13 How many cubes of side 15 cm can be fitted into a box which measure 1.5 m × 90 cm × 75 cm ?
(A) 120 (B) 300 (C) 140 (D) 100
Q.14 The edge of cube is 20 cm. How many small cubes of 5 cm edge can be formed from this cube ?
(A) 4 (B) 32 (C) 64 (D) 100
Q.15 Length and breadth of a rectangle is x and y, the its perimeter is :
(A) xy (B) x + y (C) 2(x + y) (D) 2xy
Q.16 Perimeter of an equilateral triangle of side x is :
(A) x3 (B) x2 (C) 3x (D) 2x
Q.17 The length and breadth of rectangle are 10 cm and 6 cm respecitively. Its area will be :
(A) 36 cm2 (B) 60 cm2 (C) 100 cm2 (D) 16 cm2
Q.18 Area of square of side 5 cm is :
(A) 25 sq cm (B) 10 sq cm (C) 20 sq cm (D) none of these
Q.19 The cost of flooring a room at Rs. 25 per m2 is Rs.625.
The area of the floor is :
(A) 25 m2 (B) 15 cm2 (C) 50 cm2 (D) 25 cm2
Q.20 The length of a rectangle having area 340 cm2 and breadth 20 cm is :
(A) 170 cm (B) 15 cm (C) 17 cm (D) 20 cm
Q.21 To find the distance around the figure we find its :
(A) area (B) perimeter (C) both (D) none of these
Q.22 The side of regular pentagon having perimeter 5x units is :
(A) 25 units (B) x units (C) 5 units (D) none of these
Q.23 If the side of the square field is doubled, then its area will be :
(A) four times (B) doubled (C) halved (D) tripled
Q.24 To calculate length of rectangle we divide its area by its :
(A) breadth (B) length (C) perimeter (D) 2
SUBJECTIVE TYPE
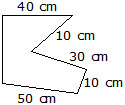
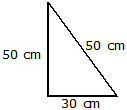
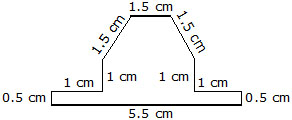
Q.1 Calcualte the perimeter of the following figures.
(A)
(B)
(C)
(D)
(E)
(F)
(G)
(H)
Q.2 A square sheet of paper has a perimeter of 40 cm. What is the length of its side ?
Q.3 Anand's garden is 70 m long and 50 m wide and is in the from of a rectangle. If he uses three of barbed wire to fence the garden, what is the total length of the wire used ?
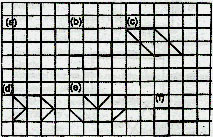
Q.4 Find the area of each of the figure drawn on squared paper in given figure. Area of each square is 1 cm2.
Q.5 The length of a rectangular field is 300 m and its breadth is its length. If a road of width 10 m is built along the inner wall of the field, what is the area of the road ?
Q.6 The area of a square picture is 441 sq. cm. What is the length of its side ?
Q.7 A marble tile measure 10 cm × 12 cm. How many tiles will be required to cover a wall is size 3 m × 4m ?
Q.8 How many envelope of size 15 cm × 20 cm can be made out of a paper of size 4 m × 6 m ?
Q.9 Five square flower beds each of side 1.2 m are dug on a piece of land 4.8 m long and 4.2 wide.
What is the area of the remaining part of the land ?
Q.10 The area of rectangular field is 594 square metre. Its breadth is 22 m. Find its perimeter.
Q.11 The area of a triangle, whose base and the corresponding altitude are 15 cm and 7 cm, is equal to a right triangle whose one of the sides containing the right angle is 10.5 cm. Find the other side of this triangle.
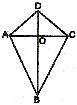
Q.12 Calculate the area of the quadrilateral ABCD as shown in figure, given that BD = 42 cm, AC = 28 cm, OD = 12 cm and AC PERPENDICULAR TO BD.
Q.13 Find the area of the shaded figure, where BAP = 90º & CDP = 90º.
Q.14 An open box is made of a thin cardboard (negligible thickness of cardboard). It is 8 cm long, 6 cm wide and 5 cm high. It is without a lid. Find the total surface area of the box.
Q.15 Three cubes, each having an edge 4 cm, are joined together. Find the surface area of the cuboid thus formed. Is this surface area equal to the sum of the surface areas of the three separate cubes ?
Q.16 Calculate the area of the shaded region in each of the following figures.
OBJECTIVE :
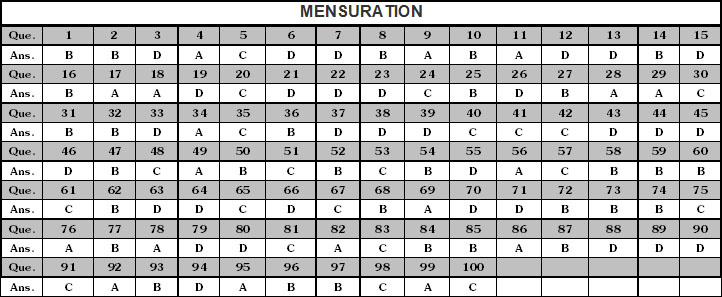
1. B 2. D 3. B 4. B 5. B 6. A 7. A 8. B 9. D 10. D
11. C 12. D 13. B 14. C 15. C 16. C 17. B 18. A 19. A 20. C
21. B 22. B 23. A 24. A
SUBJECTIVE :
1. (a) 220m (b) 420m (c) 21cm (d) 230cm
(e) 50cm (f) 160cm (g) 130cm
2. 10cm
3. 720m
4. (a) 9cm2 (b) 5cm2 (c) 4cm2 (d) 4cm2
(e) 6cm2 (f) 5cm2
5. 9600m2
6. 21cm
7. No. of tiles = 1000
8. No. of envelopes = 800
9. 12.96 sq m
10. 98m
11. 10cm
12. 588cm2
13. 625cm2
14. 188cm2
15. 224cm2 No, the surface area of cuboid and 3 cube are not equal
16. (i) 60m2 (ii) 74cm2 (iii) 44m2 (iv) 5.76m2
1. What is the length of the greatest rod that can be placed in a room whose length is 10 m, breadth 8 m and height 6 m. Given that = 1.42 .
(A) 13.2 (B) 14.2 (C) 15.2 (D) 16.2
2. Two cubes, each of edge 12 cm are joined end to end. Find the surface area of resulting cuboid.
(A) 1450 cm2 . (B) 1440 cm2 (C) 1420 cm2 (D) 1410 cm2
3. Three cubes whose edges are 3 cm, 4 cm and 5 cm respectively are melted to fo a single cube. Find the surface area of the new cube.
(A) 210 cm2 (B) 213 cm2 (C) 224 cm2 (D) 216 cm2
4. Three cubes of metal whose edges are in the ratio 3 : 4 : 5 are melted down into a single cube whose diagonal is 12X31/2 cm. Find the edge of smallest of the three given cubes.
(A) 6 cm (B) 7 cm (C) 8 cm (D) 9 cm
5. If the radius of the base of the right circular cylinder is reduced by 50%, keeping the same height, what is the ratio of the volume of the reduced cylinder to that of the original.
(A) 1 : 9 (B) 1 : 8 (C) 1 : 4 (D) 1 : 2
6. The radii of the two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. What is the ratio of their volumes?
(A) 20 : 27 (B) 18 : 27 (C) 15 : 21 (D) 11 : 15
7. The volume of the metallic cylindrical pipe is 748 cm3. Its length is 14 cm and its external radius is 9 cm. Find its thickness.
(A) 4 (B) 3 (C) 2 (D) 1
8. Find the number of coins 1.5 cm in diameter and 0.2 cm thick to be melted to form a right circular cylinder whose height is 8 cm and diameter 6 cm.
(A) 620 (B) 640 (C) 660 (D) 680
9. The vertical height of a conical tent is 42 dm and its diameter of the base is 54 dm. How many persons can it accommodate if each person is to be allowed 2916 dm3 of space? (Pie = 22/7)
(A) 11 (B) 10 (C) 9 (D) 8
10. A piece of metal in the form of a cone of radius 3 cm and height 7 cm melted and cast into a cube. Find the side of cube (nearest to a whole number)
(A) 5 cm (B) 4' cm (C) 3 cm (D) 2 cm
11. A right circular cylinder and a right circular cone have equal bases and equal heights. If their curved surfaces are in the ratio 8 : 5, what is the ratio of their base to their heights?
(A) 3 : 4 (B) 5 : 4 (C) 6 : 7 (D) 9 : 8
12. Three solid spheres of gold whose radii are 1 cm, 6 cm and 8 cm respectively are melted into a single solid sphere. Find the radius of the sphere.
(A) 6 cm (B) 7 cm (C) 8 cm (D) 9 cm
13. It needs 50 ml paint for painting a picture 50 cm × 25 cm. How much paint is needed to paint a similar picture 100 cm × 50 cm?
(A) 100 ml (B) 400 ml (C) 750 ml (D) 200 ml
14. The sides of a rectangular plot are in the ratio of 4 : 3 and its area is 1452 m2. Find the cost of fencing it at Rs 2.50 P per metre.
(A) Rs. 480 (B) Rs. 385 (C) Rs.375 (D) Rs. 365
15. How many metres of carpet 50 cm wide will be required to cover the floor of a room 30 m × 20 m?
(A) 1000 (B) 600 (C) 2400 (D) 1200
16. A room is 15 metres long, 4 metres broad and 3 metres high. Find the cost of white washing its four walls at 50 P. per m2. '
(A) Rs. 60 (B) Rs. 57 (C) Rs.55 (D) Rs. 52
17. The area of four walls of a room is 120 m2 and its length is twice the breadth, the height being 4 metres. Find the area of the floor.
(A) 50 m2 (B) 60 m2 (C) 75 m2 (D) 100 m2
18. Find the cost of fencing a circular field at the rate of 50 P. per metre if its area is 13860 m2. (p = 22/7)
(A) Rs. 660 (B) Rs.540 (C) Rs. 700 (D) Rs. 800
19. The inside circumference of a circular field is 1188 m. A road 7 m wide is constructed on the outside. Find its area.
(A) 8070 m2 (B) 8270 m2 (C) 8370 m2 (D) 8470 m2
20. The area of two circular fields is in the ratio 16 : 49. If the radius of the latter is 14 m, what is the radius of the former?
(A) 32 m (B) 18 m (C) 8 m (D) 4 m
21. The radii of the two circular field is in the ratio 3 : 5. The area of the first field is what percent less than the area of the second?
(A) 50% (B) 60% (C) 40% (D) 64%
22. What is the radius of a circular field whose area is equal to the sum of the areas of the three circular fields with radii 4 m, 4.5 m and 6 m respectively?
(A) 9 m (B) 10.5 m (C) 10 m (D) 8.5 m
23. If all the sides of a triangle be increased by 200 percent what is the corresponding increase in its area?
(A) 300% (B) 400% (C) 600% (D) 800%
24. How much paint is required for painting the outer surface of the water tank 2 m × 4 m × 3 m if it needs of a litre for every m2?
(A) 16 litres (B) 15 litres (C) 12 litres (D) 10 litres
25. The edge of three iron cubes are 6 cm, 8 cm, 10 cm respectively. A new cube was made by melting them. Find the edge of the new cube.
(A) 8 (B) 12 (C) 14 (D) 10
26. A closed wooden box 44 cm long, 32 cm wide and 28 cm high is made of wood 2.5 cm thick. Find the quantity of wood used.
(A) 16215 cm3 (B) 15005 cm3 (C) 16205 cm3 (D) 15205 cm3
27. The circumference of a circle is 100 cm. What is the side of a square inscribed in the circle?
28. A wire is in the form of a circle of radius 28 cm. What is the area of the square into which the wire is bent (pie = 22/7)
(A) 1936 cm2 (B) 1866 cm2 (C) 19.36 cm2 (D) none of these
29. If the length of a rectangle is increased by 50% and its breadth is decreased by 25%, what is the change percent in its area?
(A) 12.5% increase (B) 10% increase (C) 25% increase (D) 20% decrease
30. A reservoir is 45 m long and 12 m broad. How many kilo litres of water must be poured into it to raise the water level by 2 metres. [1 cub metric can contain 1 kiloliter]
(A) 540 (B) 1280 (C) 1080 (D) 1380
31. How many cubes can be cut out of a metre cube? Given that the parameter of the small cube is 48 cm.
(A) 7500 (B) 15625 (C) 9261 (D) 17576
32. A water tank whose dimensions are 1.5 m, 0.75 m and 0.48 m is full. Its contents are emptied into another empty tank whose base area is 1 m2. How much the water level shall rise?
(A) 64 m (B) 54 m (C) 5.4 cm (D) 34 cm
33. A hall is 100 m × 75 m × 22 m, the number of persons, who can be accommodated in it, each requiring 50 m3 of air are :
(A) 2200 (B) 1100 (C) 2500 (D) 3300
34. The diagonal of cube is 15 m, what is its volume?
(A) 375*31/2 m3 (B) 375 m3 (C) 125*31/2 m3 (D) 750*31/2m3
35. A cubic metre of a certain metal is hammered to from a fine sheet so as to cover one hectare of land. What is the thickness of the sheet?
(A) 1 cm (B) 0.1 cm (C) 0.01 cm (D) 0.001 cm
36. A conical flask of radius r and height h is full of water. It is emptied into another cylindrical flask of radius xr. If this flask becomes full, what is its height?
(A) 3x2h (B) h/3x2 (C)xh/3 (D) 3h/x
37. It is required to construct a conical circus tent of radius 21 m and 35 m slant height. The width of the canvas cloth is 3 metre, what will be the length of the cloth which shall do the needful.
(A) 700 m (B) 1250 m (C) 776.5 m (D) 770 m
38. Two spheres have volumes in the ratio 64 : 729. If 160 ml paint is required for painting the surface area of the smaller sphere, how much paint is required to paint the larger one?
(A) 729 ml (B) 750 ml (C) 216 ml (D) 810 ml
39. The diagonal of a square A is a + b, the diagonal of a square B with twice the area of A is :
(A) 2 (a + b) (B) 21/2 (a + b) (C) a + 2b (D) 2a + 4b
40. The length of a rectangle is 1 cm more than its width and its perimeter is 14 cm, then the area of the rectangle is
(A) 16 cm2 (B) 14 cm2 (C) 12 cm2 (D) 10 cm2
41. If each of the dimensions of a rectangle is increased by 100%, then the area is increased by
(A) 100% (B) 200% (C) 300% (D) 400%
42. If the length of a rectangle is increased by1/3 rd and the width is decreased by 1/3rd, then the area of the rectangle is decreased by the fraction
(A) 2/3 (B) 1/6 (C) 1/9 (D) 1/8
43. The length of a given rectangle is increased by 20% and the breadth is decreased by 20%, then the area
(A) remains the same (B) increases by 5% (C) decreases by 5% (D) decreases by 4%
44. A room is rectangular in shape and has a flat roof. It is 10 m wide, 13 m long and 5 m high. It is to be painted inside and outside and on the floor but not on the ceiling, then the total area to be painted is
(A) 360 m2 (B) 460 m2 (C) 490 m2 (D) 590 m2
45. The side of an equilateral triangle are (2a – b) cm, (a + 3b) cm and (2a – 2b + 1) then the perimeter of the triangle is :
(A) 3 cm (B) 12 cm (C) 15 cm (D) 21 cm
46. In a right triangle with sides x and y, hypotenuse z, the altitude drawn on the hypotenuse is a, then
(A) xy = a2 (B)1/x+1/y=2a2 (C) 2 + y2 = 2a2 (D) 1/x+1/y=1/a2
47. If the diagonals of a rhombus are 24 dm and 10 dm, then the perimeter of the rhombus will be
(A) 68 dm (B) 60 dm (C) 52 dm (D) 50 dm
48. If the radius of the circle is increased by 100%, then the area is increased by
(A) 100% (B) 200% (C) 300% (D) 400%
49. The side of a square is 2 cm and semicircles are constructed on each side of the square, then the area of the whole figure is
(A) (4 + 2pie) cm2 (B) (4 + 4pie) cm2 (C) 4pie cm2 (D) 8pie cm2
50. The area of a square that can be inscribed in a circle of radius r is
(A) r2 (B) 2r2 (C) 4r2 (D) 1pie2
51. If the circumference of a circle is reduced by 50%, then the area will be reduced by
(A) 50% (B) 25% (C) 75% (D) 12.5%
52. The circumference of a circle is 100 cm. Then the side of a square inscribed in the circle is
53. The area of a circle inscribed in an equilateral triangle is 48p square units. Then the perimeter of the triangle is (in units)
(A) 71*31/2 (B) 48*31/2 (C) 72 (D) 36
54. The area of the largest triangle that can be inscribed in a semi circle whose radius r cm is
(A) 2 r cm2 (B) r2 cm2 (C) 2r2 cm2 (D) 1/4 r2 cm2
55. A cord in the form of a square encloses the area 'S' cm2. If the same cord is bent into the form of a circle, then the area of the circle is
56. A circular disc of radius 10 cm is divided into sectors with angles 120° and 150°, then the ratio of the areas of two sectors is
(A) 4 : 5 (B) 5 : 4 (C) 2 : 1 (D) 8 : 7
57. The areas of three adjacent faces of a cuboid are x, y and z, then the volume of the cuboid is :
58. Three metal cubes of volume 125 cm3, 64 cm3 and 27cm3 are melted to form a new cube, then the edge of the new cube formed is
(A) 12 cm (B) 6 cm (C) 20 cm (D) 10 cm
59. If 'l', 'b' and 'h' of a cuboid are increased, decreased and increased by 1%, 3% and 2% respectively, then the volume of the cuboid
(A) increases (B) decreases
(C) increases or decreases depending on original dimensions (D) can't be calculated with given data
60. A metal pipe has an external diameter of 4 cm and internal diameter of 3 cm and is 20 cm long, then the volume of the metal used is
(A) 22 cm3 (B) 110 cm3 (C) 220 cm3 (D) 440 cm3
61. A rectangular paper of dimensions 6 cm and 3 cm is rolled to form a cylinder with height equal to the width of the paper, then its base radius is
(A) cm (B) crn (C) cm (D) cm
62. A conical container of base radius 'r' and height 'h' is full of water which is poured into a cylindrical container of radius mr, then it will occupy a height equal to
(A) 3m2h (B) h/3m2 (C) mh/3 (D) 3h/m
63. The volume of a sphere of diameter 2p cm is given by
64. The radius of a solid sphere is 'r' cm. It is bisected, then the total surface area of the two pieces obtained is
65. The radius of a sphere is increased by 50%, then the increase in surface area of a sphere is
(A) 200% (B) 150% (C) 125% (D) 50%
66. If the volume in m3 and the surface area in m2 of a sphere are numerically equal, then the radius of the sphere in m is
(A) 4 (B) 2 (C) 3.5 (D) 3
67. A sphere of radius 5 cm weights 4.4 kg, then the weight of a sphere of the same material whose radius is 3 cm is
(A) 2.64 kg (B) 1.584 kg (C) 0.9504 kg (D) 4/3(0.9504) kg
68. The volume of a sphere is r3 cubic units, then the ratio of the volume of a cube to that of a sphere which will fit inside the cube is
69. If S1 and S2 be the whole surface of a sphere and the curved surface of circumscribed cylinder, then S1 is equal to
(A) S2 (B) 2S2 (C) 2S2 (D) S2
70. A sphere has the same volume as a cylinder whose height is equal to the diameter of its cross section, then the ratio of their radii is
71. A right circular cone and a cylinder have a circle of unit radius as base and thel heights are equal to the radius itself and a hemisphere has the same radius, then their volumes are proportional respectively to
(A) 1: 2 : 3 (B) 3: 2 : 1 (C) 2: 1 : 3 (D) 1: 3 : 2
72. In the case of cuboid, No denotes the number of vertices, N1 the number of edges and N2 the number of faces, then
(A) N0 + N1 = N2 + 2 (B) N0 + N2 = N1 + 2 (C) N1 + N2 = N0 + 2 (D) N1 + N2 = 2N0
73. If the diagonal of a rectangle is twice one of the sides, then the ratio of the sides of the rectangle is
74. The length of a rectangle exceeds its breadth by 3 cm. If the numerical values of the area and the perimeter of the rectangle are equal, then the breadth of a rectangle will be
(A) 2 cm (B) 3 cm (C) 1 cm (D) 5 cm
75. If the length of every side of a triangle is increased by 50%, then the area of the triangle will be increased by
(A) 50% (B) 100% (C) 125% (D) 150%
76. If the area of a circle is halved when its radius is decreased by n, then the radius is equal to
77. If the number of units in the circumference of a circle is same as the number of units in the area, then the radius of the circle will be
(A) 1 unit (B) 2 units (C) 3 units (D) 4 units
78. The side of a square is 2 cm. Semicircles are constructed on two sides of the square, then the area of the whole figure is
79. A piece of wire 132 dm long is bent successively in the shape of an equilateral triangle, a square, a regular hexagon and a circle. Then the area included is largest when the shape is
(A) triangle (B) square (C) hexagon (D) circle
80. A wire, in the shape of an equilateral triangle, encloses an area '5' cm2. If the same wire is bent to form a circle, then the area of the circle will be
81. Two cubes have volumes in the ratio 1 : 27, then the ratio of the area of the face of one to that of the other is
(A) 1: 3 (B) 1: 6 (C) 1: 9 (D) 1: 18
82. The ratio of the height of a circular cylinder to the diameter of its base is 1 : 2, then the ratio of the areas of its curved surface to the sum of the areas of its two ends is
(A) 1: 1 (B) 1: 2 (C) 2:1 (D) 1: 3
83. The curved surface of a circular cylinder of height 'h' and the curved surface area of the cone of slant height '2h' having the same circular base, are in the ratio of
(A) 1 : 2 (B) 2 : 1 (C) 1 : 1 (D) 1 : 3
84. The volume of the greatest sphere cut off from a cylindrical wood of base radius 1 cm and height 5 cm is
85. A solid cylinder of glass whose diameter is 1.5 m and height 1 m is melted and recasted into a sphere, then the radius of the sphere is
(A) 1 m (B) 0.75 m (C) 1.25 m (D) 1.5 m
86. The perimeter of a right angled triangle is 60 cm and its hypotenuse is 26 cm, then the area of the triangle is
(A) 120 cm2 (B) 121 cm2 (C) 119 cm2 (D) 125 cm2
87. The side of a regular hexagon is 'p' cm, then its area is
88. If every side of a triangle is doubled, then the area of the new triangle is 'K' times the area of the old one. The value of K is
(A) 2 (B) 3 (C) 21/2 (D) 4
89. If the longer side of a rectangle is doubled and the other reduced to half, then the area of the new rectangle goes up by
(A) 50% (B) 100% (C) 150% (D) no change
90. If a rectangle of sides 5 cm and 15 cm is to be divided into three squares of equal area, then the sides of the squares will be
(A) 4 cm (B) 6 cm (C) 7 cm (D) none
91. Three cubes of metal whose edges are 3 cm, 4 cm and 5 cm are melted to form a new cube whose side is
(A) 4 cm (B) 5 cm (C) 6 cm (D) 12 cm
92. A closed tea box has 47 cm × 47 cm × 60 cm internal dimensions, then the total area of tin foil needed for lining it is
(A) 1.57 m (B) 1.81 m (C) 1.46 m (D) 2.10 m
93. The length, breadth and height of a cuboid are in the ratio of 5 : 4 : 2 and the total surface area is 1216 cm2, then the volume of the cuboid is
(A) 2460 cm3 (B) 2560 cm3 (C) 2660 cm3 (D) 2700 cm3
94. A wood 1 cm thick required to make a box of dimensions 24 cm × 22 cm × 17 cm, is
(A) 2276 cm3 (B) 2500 cm3 (C) 2600 cm3 (D) 2376 cm3
95. The volume of a solid cubical box whose surface area is 600 cm2 is
(A) 1000 cm3 (B) 1200 cm3 (C) 1100 cm3 (D) 900 cm3
96. If two cubes each of side 12 cm are joined end to end, then the surface area a the resulting cuboid is
(A) 1728 cm2 (B) 1440 cm2 (C) 1445 cm2 (D) 1450 cm2
97. The number of bullets of radius 2 cm that can be made from a cube of lead whose side is 44 cm is
(A) 2540 (B) 2541 (C) 2560 (D) 2575
98. If the radius of a lead shot 9 cm is melted and recasted into a right circular cylinder of height 8 cm and radius 6 cm, then the internal radius of the shot is
(A) 6 cm (B) 7 cm (C) 8 cm (D) 9 cm
99. If a sphere has the same curved surface area as total surface area of cone of vertical height 40 cm and radius 30 cm, then the radius of the sphere is
(A) 10*61/2 cm (B) 10*31/2 cm (C) 10*1/2cm (D) 12 cm
100. If the sphere of radius 6 cm is melted and drawn into a wire of radius 0.2 cm, then the length of the wire is
(A) 75 cm (B) 72 cm (C) 72 m (D) 75 m