LINES SEGMENT
In the given fig. l is a line and A and B are two points on it. The portion of the line from A to B is a line segment AB.
NOTE :
(a) Two distinct points in a plane determine one and only one line segment.
(b) A line segment is completely known if its end points are given.
(c) A line segment has length but no breadth or thickness.
Comparison of line segments :
Comparison of two line segments means finding an order (relation) between their lengths, i.e., which of them is longer than the other.
(Comparison by observation)
The method of comparing two segements by observations is not always correct. Therefore, we need a better method.
Comparison by divider or compass :
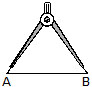
The line segments are compared with the help of a divider or a pair of compasses.
SETP 1. Place the end points of one arm of the devider at A.
SETP 2. Open the divider so that the end end points of the other arm reaches the other point B.
SETP 3. Lift the divider and without disturbing its opening, place the end points of one arm at P.
Now three cases might arise :
Case 1. The second arm of the divider falls on Q. In this case, we say that the length of AB and PQ are equal i.e AB = PQ.
Case 2. The second arm falls, at a point R between P and Q. In this case, we conculde that AB is shorter than PQ i.e AB < PQ.
Case 3. The second arm falls at a point M outside PQ. In this case, we conclude that AB is longer than PQ and AB > PQ.
Units for measurment of line segments :
In 1962 india started adopting S.l. units and the unit of measurment of length was changed to metre.
A metre is divided into 100 equal parts, each called a centimetre. A centimetre is further subdivided into 10 equal parts, each called a millimetre.
10 Millimetres (mm) = 1 Centimetre (cm)
10 Centimetres (cm) = 1 Decimetre (dm)
10 Decimetres (dm) = 1 Metre (m)
or,
1 metre = 10 decimetres
= 100 centimetres
= 1000 millimetres
Lengths of the segements in geometry are measured with the help of a straight edged ruler.
Measurement of Length of A segment :
(a) Using a ruler :
(b) Using a divider or a compass
(a) Using a ruler :
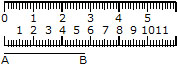
Suppose we have to measure the length of a given segment AB. Take a rule with centimeter marks and place it along the segment AB such that the zero mark on the ruler is just at A as shown in the figure.
Now read the mark on the ruler which corresponds to B. In this figure we see that the mark corresponding to B is the eighth small division after 5, i.e. AB contains 5 full centimeters and 8 millimeters.
We say that the length of AB is 5.8 cm and write it as AB = 5.8 cm.
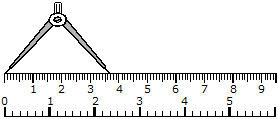
(b) Using a divider or a compass :
We open the divider such that the point of one arm is at A and the second exactly at B, i.e. the segment AB is contained in the divider. Now lift the divider carefully without disturbing its opening and place it on the ruler so that one point of the divider is at zero (0) mark. We then read the mark which corresponds to the second point of the divider.
In the adjoining figure the second point of the divider is at the seventh mark after 3, i.e. AB contains 3 complete centimeters and seven=tenths of a centimeter. We say that AB is 3 cm and 7 mm and write it as AB = 3.7 cm.
Congruent Segments :
Two segments are equal or congruent if they are of the same length.
Ex. If B is the mid point of AC and C is the mid-point of BD where A, B, C and D are collinear, show that AB = CD?
Sol. B is the mid-point of AC
\ AB = BC ....... (i)
Again C is the mid-point of BD
CD = BC ..........(ii)
From (i) and (ii), we get
AB = CD
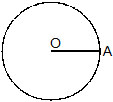
Magnitude of An angle :
Magnitude of an angle is the amount of rotation through which one of the arms must be rotated about the vertex to bring it to the position of the other arm.
Degree measure of an Angle :
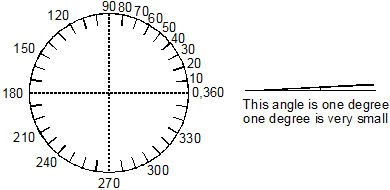
Many centuries ago in Babylonia, it was decided to divide circles into 360 equal parts and to use one of the 360 parts, or , as a unit. This unit is still used today and is called degree.
Instead of spelling out the words degree or degrees, we usually use the sign(º).
The drawing above shows a circle divided into 360 equal parts. The numerals label the marks for each of 10 arcs, beginning at 0. The arc from 0 to 1 is a 1 degree arc. 1º is read "one degree". The arc from 0 to 10 is a 10-degree arc.
Ex. What is the measure of the arc from 0 to 20 ?
Sol. The measure of the arc from 0 to 20 is 20º
Ex. What fractional part of the circle is the 90 – degree arc from 0 to 90 ?
Sol. , i.e.
Ex. Is a 180-degree arc, of the circle ?
Sol. =
Yes, 180-deree arc is of the circle.
The following illustrates the number of degrees in angles of standard rotations.
Starting position (0º)
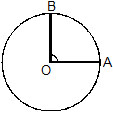
rotation (90º)
rotation (180º)
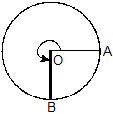
rotation (270º)
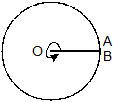
1 complete rotation (360º)
Ex. What fraction of a revolution does the hour hand of a clock turn clockwise when it goes from
(a) 3 to 9 (b) 6 to 3 (c) 2 to 5
Sol. (a) Half (b) 3 quarters (c) quarter
Ex. Where will the hour hand of a clock stop if it starts at :
(a) 12 and makes revolution, clockwise
(b) 5 and makes revolution, clockwise
(c) 7 and makes revolution, clockwise
Sol. (a) For 1 revolution, hour hand takes 12 hours
For revolution, hour hand takes × 12 or 6 hours.
It will stop at 6.
(b) For revolution, hour hand takes × 12 or 3 hours.
It will stop at 8.
(c) For revolution, hour hand takes × 12 or 9 hours.
\ It will stop at 4.
Ex. How many degrees are there in 2 right angles ?
Sol. 1 right angle = 90º
2 right angles = 2 × 90º = 180º
Congruent Angles :
If the measures of two angles are equal, the angles are called Congruent (or equal) angles.
For example, if ÐABC = 45º and ÐDEF = 45º, then ÐABC = ÐDEF i.e. ÐABC is congruent to ÐDEF.
Kinds of Angles :
Angles are classified according to their degree measure.
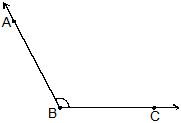
(a) An angle with measures greater than 0º and less than 90º is called an acute angle. In Fig. ABC is an acute angle.
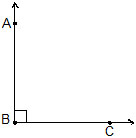
(b) An angle which measures 90º is called a right angle. In Fig. ABC is a right angle.
(c) An angle which measures greater than 90º and less than 180º is called an obtuse angle. In Fig. ABC is an obtuse angle.
(d) An angle which measures 180º is called a straight angle in figure. ÐABC is a straight angle.
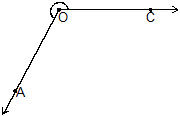
(e) An angle with measure greater than 180º and less than 360º is called a reflex angle. ÐAOC is a reeflex angle.
(f) An angle which measures 360º is called a complete angle. ÐAOB is complete angle.
(g) An angle which measures 0º is called a zero angle. ÐAOB is a zero angle.
CLASSIFICATION OF TRIANGLES
We know that a triangle is a polygon of 3 sides. It has 3 angles and 3 sides. So we classify triangles according to sides as well as according to angles.
According to sides, the triangle are
(a) Scalene Triangle : If all the sides of a triangle are unequal in length, it is called a scalene triangle.
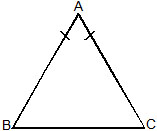
(b) Isosceles Triangle : If two sides of a triangle are equal. It is called isosceles triangle.
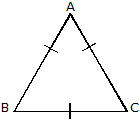
(c) Equilateral Triangle :
If all the three sides of triangle are equal, it is called equilateral triangle.
AB = AC = BC, so DABC is an equilateral triangle.
According to angles, the triangles are
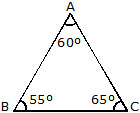
(a) Acute angled Triangle : A triangle whose all angles are acute is known as an acute angled triangle or simply acute trinagle.
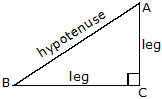
(b) Right angled Triangle : A triangle whose one of the angles is a right angle is called a right angled triangle or simply a right triangle.
The side opposite to the right angle is called the hypotenuse and the other two sides are called the legs of the triangle.
(c) Obtuse angled Triangle : A triangle whose one of the angles is obtuse angle is called on obtuse angled triangle or simply obtuse triangle.
Reaction between Sides and Angles of a Triangle :
(a) The angles of a scalene triangle are unequal.
(b) In an isosceles triangle, two angles are equal.
(c) All the angles of an equilaterial triangle are equal.
(d) If two angles of a triangle are equal then the the sides opposite to them are also equal.
(e) A right angled triangle with two sides equal is called an isosceles right angled triangle.
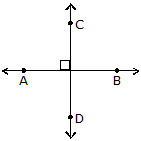
PERPENDICULAR LINES
Two lines are said to be perpendicular if the angle between them measure 90º. Line AB is perpendicular to CD, also we can say line CD is perpendicular to AB.
Represented as ^
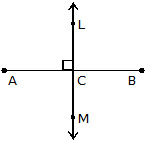
PERPENDICULAR BISECTOR
A line perpendicular to the given line segment as well as bisects it, is called perpendicular bisector. Line LM is perpendicular bisector of line segment AB.
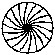
CLASSIFICATION OF QUADRILATERAL
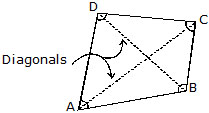
We know that a quadrilateral is a polygon of 4 sides. In other words, a quadrilateral is a closed plane figure with four sides. A quadrilateral is named by taking its vertices in order either clockwise or anticlockwise direction. ABCD is a quadrilateral. The line segments AC and BD are its diagonals.
The classification of six types of quadrilaterals is summarised below :
Parallelogram : 2 pair of opposite sides parallel
Trapezium : 1 pair of opposite sides parallel
Rectangle : Parallelogram with 4 angles right angles
Rhombus : Parallelogram with all 4 sides equals
Square : Rhombus with 4 angles right angles
Kite : 2 pair of adjacent sides equal
POLYGON
A polygon is a plane closed figure made up of lines segments.
The minimum number of sides of a polygon is 3. A polygon can have more than 3 sides.
NOTE :
Number of sides of a polygon are equal to its number of angles.
Classification of polygons :
We name the polygon according to the number of sides as follows :
No. of sides Name
3. Triangle
4. Quadrilateral

5. Pentagon
6. Hexagon
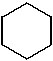
7. Heptagon
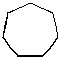
8. Octagon
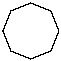
9. Nonagon
Regular polygon :
A polygon is called regular if all its sides are equal in length and all angles are equal in measure.
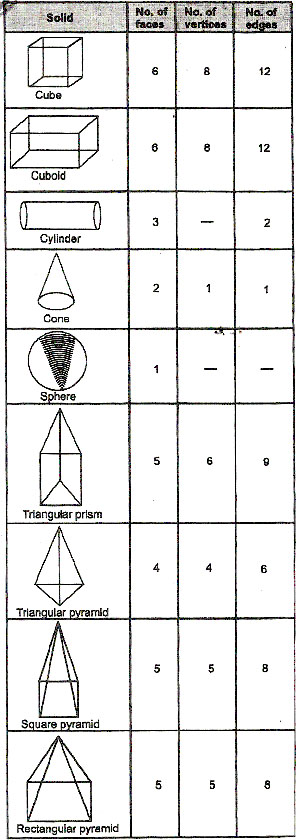
SOLID FIGURES
A Closed figure which lies in more than one plane is called a space figure or a solid figure.
The figures such as cube, cuboid, cylinder, pyramid, etc., which have three dimensions, namely length, breadth and height are called solid figures or 3-dimensional figures.
Solid figures (Three dimensional figures)
Faces, Edges and vertices of Solid Figure
· The surface of a solid is called its face.
· An edge is a line segment that is the intersection of two faces.
· A corner or vertex in a solid shape is the point where the faces meet.
TYPES OF SOLID
There are mainly three types of solids :
(a) Prism : A solid whose base and top are identical polygons and side faces are rectangles, is called a prism. In a square prism whose base and top are congruent squares. Cuboid, cube etc. are all special types of prisms.
(b) Pyramid : A solid whose base is any polygon and side faces are triangles, is called a pyramid.
Figure shows a pentagonal pyramid.
(c) Sphere : sphere is a solid whose every point is equidistant from a fixed point. Figure shows the sphere.
NOTE :
(i) All the side faces of a pyramid (triangular, rectangular, squares, pentagonal etc.) are triangular.
(ii) A pyramid is named according to the shape of its non-triangular face. If all the faces are triangular, then it is called a triangular pyramid or tetrahedron.
Cuboid :
A cuboid has
(i) 6 rectangular faces
(ii) 12 edges
(iii) 8 vertices.
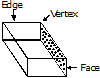
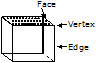
Cube (Square prism) :
A cube has
(i) 6 square faces
(ii) 12 edges
(iii) 8 vertices
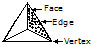
Triangular Pyramid :
A triangular pyramid (Tetrahedron) shown in fig. has :
(i) 4 faces
(ii) 6 edges
(iii) 4 vertices
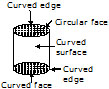
Cylinder : A cylinder has
(i) no vertex
(ii) two circular faces
(iii) one curved face
(iv) two curved edges
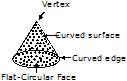
Cone : A cone has
(i) one vertex
(ii) one curved edge
(iii) one curved face and one flat face
· Following table provides the details of the number of faces, edges and vertices of some solids.

 Starting position (0º)
Starting position (0º) rotation (90º)
rotation (90º) rotation (180º)
rotation (180º) rotation (270º)
rotation (270º) 1 complete rotation (360º)
1 complete rotation (360º)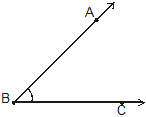
.JPG)