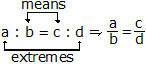RATIO
Ratio : A comparison by division is called ratio. A ratio is usually denoted by the symbol (:). If a and b (b is not equal to 0) are two quantities of the same kind, then the fraction a/b is called the ratio of a to b, we write it as a : b.
or = a/b=
In the ratio a: b, the first term is 'a' and the second term is 'b'. A ratio is said to be in the simplest form if its two terms have no common factor other than 1.
NOTE :
(i) The ratio of two numbers is usually expressed in its simplest form.
(ii) In a ratio, we compare two quantities. The comparison becomes meaningless if the quantities being compared are not of the same kind i.e. they are not measured in the same units.
(iii) It is just meaningless to comeare 20 bags with 200 crows. Therefore, to find the ratio of two quantities, they must be expressed in the same units.
(iv) Since the ratio of two quantities of the same kind determines how many times one quantity is contained by the other. So the ratio of any two quantities of the same kind is an abstract quantity.
In other words, ratio has no unit or it is independent of the units used in the quantities compared.
(v) The order of the terms in a ratio a : b is very important. The ratio 3 : 2 is different from the ratio 2 : 3.
(vi) We can multiply or divide both the terms of the ratio by a non zero number which does not alter the value of the ratio.
RATIO IN THE SIMPLEST OR LOWEST FORM
A ratio a/b or a : b is said to be in its lowest or simplest form if a and b have no common factors except 1.
For example,
40 : 80 =
= 1/2 = 1 : 2
10000 : 8000 =
= 5/4 = 5 : 4
STEPS :
(a) Write the ratio as a fraction.
(b) Divide the numerator and the denominator by their HCF.
(c) The answer is a fraction in its lowest form ; so change it to ratio, which will be in the lowest form.
Ex. Express the following ratio in their simplest form :
(a) 150 : 400
(b) 85 : 225
Sol. (a) 150 : 400 =
= 3/8 = 3 : 8
(b) 85 : 255 =
= 1/3 = 1 : 3
Ex. Find the ratio of the following :
(a) 36 minutes to 2 hours.
(b) 50 cm to 5 metres.
(c) 32 g to 1 kg
(d) 3 days to 1 years.
Sol. (a) Change both 36 minutes and 2 hours to the same unit.
Now, 36 minutes = 36 minutes
2 hours = 2 × 60 minutes = 120 minutes
Ratio of 36 minutes to 2 hours
36 : 120 =
= 3/10 = 3 : 10
(b) First convert both into numbers with the same unit.
50 cm = 50 cm
5 metres = 500 cm
Hence ratio of 50 cm to 5 metes is
= 50 : 500 =
= 1/10 = 1 : 10
(c) First convert both into numbers with the same unit.
32 g = 32 g
3kg = 3000 g
Ratio = 32 : 3000 =
= 4/375= 4 : 375
(d) First, convert both into numbers with the same unit.
3 days = 3days
1 year = 365 days
Ratio = 3 : 365
Comparison of Ratios :
1. Write the given ratios as fractions in the simplest form.
2. Find the LCM of the denominators of the fractions.
3. Convert them into like fractions with same denominators.
4. Compare the numerators and arrange the fractions.
5. Then respective ratios are also in the same order.
Ex. Compare 5 : 12 and 3 : 6
Sol. 5 : 12 = 5/12, 3 : 8 =3/8
LCM of 8, 12 = 24
5 : 12 = 5/12 ×2/2 =10/24
3 : 8 = 3/8 ×3/3 =9/24
9/24< 10/24
3/8 < 5/12 OR 3 : 8 < 5 : 12
Ex. The ratio of the number of girls to the number of boys in a school is 5 : 8. In another school the ratio of the number of girl to the number of boys is 7 : 10. Which school has a higher ratio of girls?
Sol. The ratios of girls to boys in the two schools are 5 : 8 and 7 : 10. Since the number of girls forms the numerator in both the cases, the school which has a greater ratio has a higher number of girls. We have two fractions 5/8 and 7/10 . We can compare these fractions by converting both the fractions into fractions with same denominator.
The LCM of 8 and 10 is 40.
5/8 = 5×5/8×5 =25/40 , 7/10×4/4 = 28/40
28/40> 25/40
So the second school with the ratio 7 : 10 has a higher ratio of girls.
Ex. Mr. Harry divided Rs. 84,630 between Shinchan and Nimavari in the ratio 3 : 4. How much did each of them get?
Sol. Ratio of money between Shinchan and Nimavari = 3 : 4
Sum of the terms of the ratio = 3 + 4 = 7
Sinchan's share = 3/7 of total money
Nimavari's share = 4/7 of total money
The amount of money Shinchan's gets
= 3/7 × Rs. 84,630
= Rs. 36, 270
The amount of money Nimavari gets
= 4/7 × Rs. 84,630
= Rs. 48,360.
Ex. The number of stamps in the collections of Suniyo, Lobita, and Suzuka are in the ratio 3 : 4 : 5. If lobita has a collection of 108 stamps, find the number of stamps that Suniyo, and Suzuka each has.
Sol. The number of stamps in the collections of Suniyo Lobita, and Suzuka are in the ratio = 3 : 4 : 5.
Sum = 3 + 4 + 5 = 12
Let the number of stamps with Suniyo be 3x. Then Lobita will have 4x stamps and Suzuka will have 5x stamps.
Given that Lobita's 4x = 108 stamps
x = 108/4 = 27
Suniyo's 3x = 3 × 27 = 81 stamps
Suzuka's 5x = 5 × 27 = 135 stamps
Suniyo's has 81 stamps and Suzuka has 135 stamps.
EQUIVALENT RATIO
The two or more ratios are set to be equivalent if their simplest form is same.
e.g.21/35 , 12/20 are equivalent ratios
because simplest form of 31/35,12/20 is 3/5 .
Ex. If a : b = 2 : 3 and b : c = 5 : 7, find a : c & b : c.
Sol. Given a/b =2/3 and b/c = 5 : 7
a/c =
=
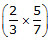
= .10/21
So, a : c = 10 : 21
Aslo, a : b = 2 : 3 and b : c = 5 : 7
LCM of 3 and 5 is 15
a/b = 2/3 × 5/3 = 10/15
b/c =5/7 × 3/3 = 15/21
a : b : c = 10 : 15 : 21.
Ex. Divide Rs. 4340 between A, B and C so that A's share : B's share : C' share = 1/2 : 1/3 : 1/5
Sol. A, B and C so that A's share : B's share : C' share = 1/2 : 1/3 : 1/5
L.C.M. 2, 3, 5 is 30
A, B and C so that A's share : B's share : C' share = 1/2 : 1/3 : 1/5
= 1/2 × 30 : 1/3 × 30 : 1/5 × 30
= 15 : 10 : 6
A share =
= × 4340 = 2100 Rs.
B share =
= × 4340 = 1400 Rs.
C share =
= × 4340 = 840 Rs.
PROPORTION
An equality of two ratios is called a proportion.
For example, 3 : 5 = 9 : 15
The first and the fourth terms are called the extremes or extreme terms. The second and the third terms are called the middle terms or means.
In case of proportion, we can say that the product of the extreme terms = the product of the middle terms.
Product of extremes = product of means
Þ a × d = b × c
Ex. If a : 30 :: 7 : 15, find the value of a.
Sol. Product of the extremes = 15a
product of the means = 30 × 7
Product of the extremes = product of the means
15a = 30 × 7
so a = 30 × 7/15 = 14
Ex. Are 36, 49, 6, 7 in proportion.
Sol. We have,
Product of extremes = 36 × 7 = 252
Product of means = 49 × 6 = 294
Clearly, Product of extremes ¹ Product of means.
Hence, 36, 49, 6, 7 are not in proportion.
Ex. 80 students consume 720 kg of wheat in a month.
How many kilograms of wheat are required in a hostel with 150 students for a month?
Sol. Let wheat required be x kg.
Students : Students :: Quantity of Wheat : Quantity of wheat
80 : 150 :: 720 : x
Product of extremes = Product of means
80x = 150 × 720
x = (150 × 720)80 = 1,350 kg.
Ex. Rajiv invest Rs. 9500 in a bank and earn interest Rs. 665. If Deepak invests in the same bank, at the same rate of interest, for the same time period, an amount of Rs.7,500, what will be the interest that he will earn?
Sol. Let the interest Deepak earns be Rs. x.
9500 : 7500 :: 665 : x
9500x = 7500 × 665
x =(7500 ×665)/9500 = Rs 525.
UNITARY METHOD
Look at this problem.
If the cost of 3 pens is Rs. 12, what will be the cost of 8 pens?
The cost of 3 pens is Rs.12. So we know that the cost of one pen will be lesser than Rs. 12. We can find the cost of one pen by dividing Rs.12 by 3. The cost of one pen is Rs.12 ¸ 3 = Rs. 4. If we have to find the cost of 8 pens, we know that it will be more than the cost of one pen. So we multiply Rs.4 by 8 and we get Rs. 32. So the cost of 8 pens is Rs. 8 × 4 = Rs. 32.
In the process of our calculation we found out the value of one unit(in this case cost of one pen)
So this method of solving is called unitary method.
Steps to follow in unitary method
1. Identify the facts given.
2. Identify what is to be found out.
3. Find the value of a unit by dividing.
Value of one = ( given value ) / number of articles
4. Multiply this result with the required units. Value of many = value of one × required no of units.
Ex. If the cost of 6 chocolates is Rs. 210, then find the value of 4 chocolates.
Sol. Cost of 6 chocolates = Rs. 210
Cost of 1 chocolates = Rs. 210/6 = Rs. 35
Cost of 4 chocolates = Rs. 35 × 4 = Rs. 140
Thus, 4 chocolates cost Rs. 140.
Ex. A bus travels 240 km in 6 hours. How long will it take to travel 360 km?
Sol. Time taken for 240 km = 6 hours
Time taken for 1 km = 6/240 hours = 1/40 hours
Time taken for 360 km = 1/40 × 360 = 9 hours.
Thus, the bus takes 9 hours to travel 360 km.
Ex. Raj earns Rs. 1500 in 10 days. How much will he earn in 45 days ?
Sol. Earning in 10 days = Rs. 1500
Earning in 1 day = 1500/10 = Rs. 150
Earning in 45 days = Rs 150 × 45 = Rs. 6750
Thus, Raj earns Rs. 6750 in 45 days.
Ex. A family of 8 people is entitled to a ratio of 6,400 grams of sugar. What will be the sugar ratio for a family of 10 people?
Sol. Quantity of sugar for 1 person = 6400/8 = 800 gm
Quantity of sugar for 10 people = 800 × 10 = 8000 gm = 8 kg.
OBJECTIVE TYPE
Q.1 If the cost of 8 Shirts is Rs. 4000, then find the cost of 3 shirts.
(A) Rs. 1000 (B) Rs. 1200 (C) Rs. 1500 (D) Rs. 500
Q.2 A scooter travels 60 km in 2 hours. How long will it take to travel 300 km ?
(A) 5 hr. (B) 8 hr. (C) 10 hr. (D) 12 hr.
Q.3 The length and breadth of rectangle are 45 cm and 30 cm find the ratio of breadth to length.
(A) 2 : 3 (B) 3 : 2 (C) 5 : 3 (D) 3 : 5
Q.4 Find the ratio of 5 days to 60 hours.
(A) 1 : 2 (B) 12 : 1 (C) 1 : 12 (D) 2 : 1
Q.5 Which one is not the equivalent ratio of 3 : 5
(A) 6 : 10 (B) 12 : 25 (C) 9 : 15 (D) 15 : 25
Q.6 If Rs. 75 is divided in the ratio 2 : 3 between Shinchan and Nimavari, then find Nimavari share.
(A) Rs. 30 (B) Rs. 45 (C) Rs. 60 (D) Rs. 50
Q.7 If 3 : x :: 12 : 20, find the value of x.
(A) 5 (B) 6 (C) 7 (D) 8
Q.8 The greatest ratio among the following ratios is :
(A) 2 : 3 (B) 40 : 25 (C) 5 : 8 (D) 75 : 21
Q.9 A perpendicular rod of length of 12 cm make 8 cm. long shadow on the ground. At the same time a tower makes 40 meter long shadow on the ground. The height of the tower will be
(A) 60 meter (B) 40 meter (C) 50 meter (D) 30 meter
Q.10 If x/y=3/2 , then (x+y)/(x-y) is equal to :
(A)4/3 (B) 1/2(C) 5/4(D) 5
Q.11 Which of the following are in proportion ?
(A) 6, 8, 2, 3 (B) 5, 10, 2, 4 (C) 9, 4, 5, 3 (D) 8, 5, 3, 6
Q.12 a, b, c, d are said to be in proportion if :
(A) a × c = b × d (B) a × b = c × d (C) a × d = b × c (D) None of these
Q.13 Ratio 9 : 12 is same as :
(A) 8 : 14 (B) 4 : 3 (C) 3 : 4 (D) 1 : 4
Q.14 If x : 15 :: 8 : 3, then the value of x :
(A) 8 (B) 32 (C) 40 (D) 20
Q.15 The ratio of 75 paise to Rs. 5 is :
(A) 15 : 1 (B) 1 : 15 (C) 3 : 20 (D) 20 : 3
Q.16 25, 45, 45, y are in proportion then value of y is :
(A) 225 (B) 5 (C) 81 (D) 45
Q.17 There are 18 boys and 14 girls in a class. The ratio of girls to boys is :
(A) 9 : 7 (B) 7 : 9 (C) 9 : 14 (D) 18 : 7
Q.18 The simplest form of 9 : 15 is :
(A) 9 : 5 (B) 15 : 9 (C) 3 : 5 (D) 5 : 3
Q.19 On comparing 7 : 21 and 3 : 5, we find that the smaller ratio is :
(A) 7 : 21 (B) 3 : 1 (C) 1 : 3 (D) (A) and (C) both
Q.20 In a basket containing 40 apples, 15 were found to be rotten. Find the ratio of rotten to fresh apples.
(A) 7 : 3 (B) 3 : 5 (C) 8 : 3 (D) 3 : 8
SUBJECTIVE TYPE
Q.1 The price ratio of one scooter and one cycle is 9 : 5. If the value of scooter is 4200 Rs. more than cycle, then find the price of cycle.
Q.2 Fill in the missing numbers :
9/12= -----/48 = 3/.......
Q.3 Present age of father is 50 years and that of his son is 15 year. Find the ratio of
(i) present age of father to the present age of son.
(ii) age of father to the age of son, when son was 10 year old.
Q.4 Shinchan earns Rs. 1000 in 5 days. How much will he earn in 15 days ?
Q.5 In a year, Harry earns Rs. 3,00,000 and saves 1,20,000. Find the ratio of
(i) Money that Harry earn to the money he saves.
(ii) Money that he save to the money he spends.
Q.6 In a school, out of 4000 students, 2400 are girls. Find the ratio of :
(i) Number of girls to the total number of students.
(ii) Number of boys to the number of girls.
Q.7 Are 30,40,45 and 60 in proportion.
Q.8 Shanta bought 72 kg wheat for Rs. 324. How many kilogram of wheat could she have bought if she had spent only Rs. 144.
Q.9 20 balloons have to be divided between Amit and Anshu in the ratio 2 : 3. How many does each receive?
Q.10 A profit of Rs. 3000 is to be divided between three persons A, B and C in the ratio 3 : 4 : 5.
Find the share of each.
Q.11 In an election between two candidates A and B, 30,000 votes polled. A won the election with the margin of 400 votes. Find the ratio of votes polled in favour of each candidates.
Q.12 A bullock-cart travels 35 km in 5 hours and a car travels 120 km in 2 hours. Find the ratio of their speeds.
Q.13 The angles of a triangle are in the ratio 3 : 2 : 1. Find the angles.
Q.14 1 score of pencils cost Rs. 12.50. How many pencils can be bought for Rs. 15? (1 Score = 20)
Q.15 4.5 g of an alloy of copper and zinc contains 3.5 g of copper. What weight of copper will be there in 18.9 g of the alloy.
Answer keys
OBJECTIVE :
1. C 2. C 3. A 4. D
5. B 6. B 7. A 8. D
9. A 10. D 11. B 12. C
13. C 14. C 15. C 16. C
17. B 18. C 19. D 20. B
SUBJECTIVE :
1. Cycle cost Rs.5250
2. 9/12=(9x4)/(12x4)=36/48;
9/12=(9÷3)/(12÷3)
3. (i) 50/15=10/3
(ii) When son was 10 at that time father was = 45 year so required ratio = 45/10=9/2
4. Earning is 5 days = Rs.1000
Earning in 1 day = 1000/5 = Rs.200
Earning in 15 days = Rs.200 × 15
= Rs.3000
Thus, Shinchan earns Rs.3000 in 15 days
5. Earning = 3,00,000
Save = 1,20,000
Expanses = Earning – Save
= 3,00,000 – 1, 20,000 = 1,80,000
(i)
(ii)
6. No. of girls = 2400
No. of boys = 4000 – 2400 = 1600
(i)
(ii)
7. We have,
Product of extremes = 30 × 60 = 1800
Product of means = 40 × 45 = 1800
Clearly, Product of extremes = Product of means
Hence, 30, 40, 45 and 60 are in proportion
8. Let the quantity of wheat that she purchased for Rs.144 be x kg.
Product of extreme = 72 × 144
Product of the middle terms = 324x
x = (72x144)/324 = 32 kg
9. 8, 12
10. Rs.750, Rs.1000 Rs.1250
11. 38 : 37
12. 7 : 60
13. 90°, 60°, 30°
14. 24 pencil
15. 14.7 gram
In questions 1 to 10, only one of the four options is correct. Write the correct one.
1. The ratio of 8 books to 20 books is
(A) 2 : 5 (B) 5 : 2 (C) 4 : 5 (D) 5 : 4
2. The ratio of the number of sides of a square to the number of edges of a cube is
(A) 1 : 2 (B) 3 : 2 (C) 4 : 1 (D) 1 : 3
3. A picture is 60cm wide and 1.8m long. The ratio of its width to its perimeter in lowest form is
(A) 1 : 2 (B) 1 : 3 (C) 1 : 4 (D) 1 : 8
4. Neelam’s annual income is Rs. 288000. Her annual savings amount to Rs. 36000. Theratio of her savings to her expenditure is
(A) 1 : 8 (B) 1 : 7 (C) 1 : 6 (D) 1 : 5
5. Mathematics textbook for Class VI has 320 pages. The chapter ‘symmetry’ runs from page 261 to page 272. The ratio of the number of pages of this chapter to the total number of pages of the book is
(A) 11 : 320 (B) 3 : 40 (C) 3 : 80 (D) 272 : 320
6. In a box, the ratio of red marbles to blue marbles is 7:4. Which of the following could be the total number of marbles in the box?
(A) 18 (B) 19 (C) 21 (D) 22
7. On a shelf, books with green cover and that with brown cover are in the ratio 2:3. If there are 18 books with green cover, then the number of books with brown cover is
(A) 12 (B) 24 (C) 27 (D) 36
8. The greatest ratio among the ratios 2 : 3, 5 : 8, 75 : 121 and 40 : 25 is
(A) 2 : 3 (B) 5 : 8 (C) 75 : 121 (D) 40 : 25
9. There are ‘b’ boys and ‘g’ girls in a class. The ratio of the number of boys to the total number of students in the class is:
(A) b/b + g (B) g / b + b (C) b/g (D) b + g / b
10. If a bus travels 160 km in 4 hours and a train travels 320km in 5 hours at uniform speeds, then the ratio of the distances travelled by them in one hour is
(A) 1 : 2 (B) 4 : 5 (C) 5 : 8 (D) 8 : 5
In questions 16 to 34, state whether the given statements are true (T) or false (F).
16.3/8=15/40
17. 4 : 7 = 20 : 35
18. 0.2 : 5 = 2 : 0.5
19. 3 : 33 = 33 : 333
20. 15m : 40m = 35m : 65m
21. 27cm2 : 57cm2 = 18cm : 38cm
22. 5kg : 7.5kg = Rs 7.50 : Rs 5
23. 20g : 100g = 1metre : 500cm
24. 12 hours : 30 hours = 8km : 20km
25. The ratio of 10kg to 100kg is 1:10
26. The ratio of 150cm to 1metre is 1:1.5.
27. 25kg : 20g = 50kg : 40g
28. The ratio of 1 hour to one day is 1:1.
29. The ratio 4 :16 is in its lowest form.
30. The ratio 5 : 4 is different from the ratio 4 : 5.
31. A ratio will always be more than 1.
32. A ratio can be equal to 1.
33. If b : a = c : d, then a, b, c, d are in proportion.
34. The two terms of a ratio can be in two different units.
In questions 35 to 46, fill in the blanks to make the statements true.
35. A ratio is a form of comparison by ______.
36. 20m : 70m = Rs 8 : Rs ______.
37. There is a number in the box such that , 24, 9, 12 are in proportion. The number in the box is_____.
38. If two ratios are equal, then they are in _____.
Use Fig. 2.1 (In which each square is of unit length) for questions 39 and 40:
39. The ratio of the perimeter of the boundary of the shaded portion to the perimeter of the whole figure is _______.
40. The ratio of the area of the shaded portion to that of the whole figure is ______.
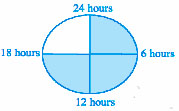
41. Sleeping time of a python in a 24 hour clock is represented by the shaded portion in Fig. 8.3.
The ratio of sleeping time to awaking time is ______.
42. A ratio expressed in lowest form has no common factor other than ______ in its terms.
43. To find the ratio of two quantities, they must be expressed in _____units.
44. Ratio of 5 paise to 25 paise is the same as the ratio of 20 paise to_____
45. Saturn and Jupiter take 9 hours 56 minutes and 10 hours 40 minutes, respectively for one spin on their axes. The ratio of the time taken by Saturn and Jupiter in lowest form is ______.
46. 10g of caustic soda dissolved in 100mL of water makes a solution of caustic soda. Amount of caustic soda needed for 1 litre of water to make the same type of solution is ______.
47. The marked price of a table is Rs 625 and its sale price is Rs 500. What is the ratio of the sale price to the marked price?
48. Which pair of ratios are equal? And why?
(i)2/3,4/6 (ii) 8/4,2/1(iii) 4/5,12/20
49. Which ratio is larger 10 : 21 or 21 : 93?
50. Reshma prepared 18kg of Burfi by mixing Khoya with sugar in the ratio of 7 : 2. How much Khoya did she use?
51. A line segment 56cm long is to be divided into two parts in the ratio of 2 : 5. Find the length of each part.
52. The number of milk teeth in human beings is 20 and the number of permanent teeth is 32. Find the ratio of the number of milk teeth to the number of permanent teeth.
53. Sex ratio is defined as the number of females per 1000 males in the population. Find the sex ratio if there are 3732 females per 4000 males in a town.
54. In a year, Ravi earns Rs 360000 and paid Rs 24000 as income tax. Find the ratio of his
(a) income to income tax.
(b) income tax to income after paying income tax.
55. Ramesh earns Rs 28000 per month. His wife Rama earns Rs 36000 per month. Find the ratio of
(a) Ramesh’s earnings to their total earnings
(b) Rama’s earnings to their total earnings.
56. Of the 288 persons working in a company, 112 are men and the remaining are women. Find the ratio of the number of
(a) men to that of women.
(b) men to the total number of persons.
(c) women to the total number of persons.
57. A rectangular sheet of paper is of length 1.2m and width 21cm. Find the ratio of width of the paper to its length.
58. A scooter travels 120km in 3 hours and a train travels 120km in 2 hours.
Find the ratio of their speeds.
[speed=distance/time taken]
59. An office opens at 9 a.m. and closes at 5.30 p.m. with a lunch break of 30 minutes. What is the ratio of lunch break to the total period in the office?
60. The shadow of a 3m long stick is 4m long. At the same time of the day, if the shadow of a flagstaff is 24m long, how tall is the flagstaff?
61. A recipe calls for 1 cup of milk for every 21/2 cups of flour to make a cake that would feed 6 persons. How many cups of both flour and milk will be needed to make a similar cake for 8 people?
62. In a school, the ratio of the number of large classrooms to small classrooms is 3:4. If the number of small rooms is 20, then find the number of large rooms.
63. Samira sells newspapers at Janpath crossing daily. On a particular day, she had 312 newspapers out of which 216 are in English and remaining in Hindi. Find the ratio of
(a) the number of English newspapers to the number of Hindi newspapers.
(b) the number of Hindi newspapers to the total number of newspapers.
64. The students of a school belong to different religious backgrounds. The number of Hindu students is 288, the number of Muslim students is 252, the number of Sikh students is 144 and the number of Christian students is 72. Find the ratio of
(a) the number of Hindu students to the number of Christian students.
ANSWER
1. (A) 2. (D) 3. (D) 4. (A) 5. (C) 6. (D) 7. (C)
8. (D) 9. (A) 10. (C) 11. 12 12. 4 13. 10 14. 18, 60
15. 28, 81, 52 16. T 17. T 18. F 19. F 20. F
21. T 22. F 23. T 24. T 25. T 26. F 27. T
28. F 29. F 30. T 31. F 32. T 33. F 34. F
35. division 36. 28 37. 18 38. proportion 39. 3 : 7 40. 1 : 6
41. 3 : 1 42. one 43. same 44. 100 paise OR 1 Rupee
45. 149 : 160 46. 100gm 47. 4 : 5 48. (i) and (ii) 49. 10 : 21 50. 14kg
51. 16cm and 40cm 52. 5 : 8 53. 933 54. (a) 15 : 1 (b)1 : 14
55. (a) 7 : 16 (b) 9 : 16 56. (a) 7 : 11 (b) 7 : 18 (c) 11 : 18
57. 7 : 40 58. 2 : 3 59. 1 : 17 60. 18 m 61.42/3 cups 62. 15
63. (a) 9 : 4 (b) 4 : 13
64. (a) 4 : 1 (b) 1 : 3