INTEGERS
We have learnt about natural and whole numbers in the previous chapters. But when we subtract a greater whole number from a smaller whole number, then the difference will not be a whole number. Hence, there is a need to extend the number system to include such numbers.
In our day-to-day life, we often come across many situation involving the use of opposites. Some of these are discussed below.
Temperature : During the winter season, the minimum temperature on a particular day, say in Chennai, may be 20ºC. This means that the temperature in Chennai is higher than the melting point of ice, which is 0ºC. On the same day, the minimum temperature in Shimla may be 5ºC below 0ºC. How do we represent this? This can be represented as –5ºC, read as minus five degree centigrade.
Height : If we say that the height of a mountain is 2,000 metres, it means that the mountain top is 2,000 metres above the mean sea level. Here, mean sea level is considered to be the zero level. Simiarly, the depth of an ocean, say 300 metres below the mean sea level, can be expressed as –300 metres high. If height is considered as positive, depth is considered as negative height and vice versa.
=Direction : If we consider the direction towards North as positive, then 5 metres north would mean 5 metres towards the north, while -5 metres north would mean 5 metres in the opposite direction of north, i.e., 5 metres towards the south. Similarly, the negative of south is the positive of north.
Profit and Loss : If a profit of Rs 10 is expressed as Rs (+ 10), then a loss of Rs 20 is expressed as Rs (– 20) profit. We can say that negative profit is positive loss and negative loss is positive Profit.
EXAMPLE. If profit is considered as positive, state the following as profit :
(a) profit of Rs 50
(b) Loss of Rs 25
Sol. (a) profit of Rs. 50 is a positive quantity. So, profit is Rs (+ 50)
(b) Loss of Rs 25 is negative profit. Hence, loss of Rs 25 = Profit of Rs (– 25)
ORDERING OF INTEGERS
(a) Negative numbers and zero lie to the left of positive numbers, so all positive integers are greater than negative integers and zero.
i.e., – 2 < 2, – 3 < 1, – 4 < 3, 0 < 2
(b) 0 (zero) lies to the right of negative integers, so 0 is always greater than the negative integers.
i.e., – 1 < 0, – 2 < 0, – 3 < 0, – 10 < 0
(c) In positive integers, a number with greater numerical value is greater as these are on the right side on the number line.
i.e., 22 > 20, 121 > 51
(d) In negative integers, a number with greater numerical value is smaller as these are farther on the left side on the number line.
i.e., – 22 < – 20, – 121 < – 51
EXAMPLE. Insert > or <.
(a) 8 – 8 (b) – 10 – 6
Sol. On the number line, –8 is on the left of zero and 8 is on the right of zero, So, 8 is greater than – 8.
(b) – 10 is on the left of – 6 on a number line.
Hence, – 10 is less than – 6.
So, – 10 – 6
EXAMPLE. Arrange the following integers in ascending order :
– 20, – 65, 25, 5, – 10
Sol. The smallest number is – 65
The next one is – 20.
The next one is – 10.
The next one is 5
and the last one is 25.
So, the numbers in ascending order are :
– 65, – 20, – 10, 5, 25
EXAMPLE. Which integer in each of the following pairs is to the right of the other on the number line ?
(a) 1, 7 (b) – 2, – 5 (c) 0, – 3 (d) – 5, 8
Sol. (a) 7 (b) – 2 (iii) 0 (d) 8
EXAMPLE. Use a number line to answer the following questions :
(i) Which number shall we reach if we move 5 numbers to the left of 3 ?
(ii) Which number shall we reach if we move 6 numbers to the right of – 3 ?
Sol. (i)
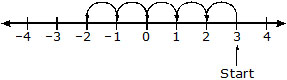
Moving 5 numbers to the left of 3, we reach the point –2.
(ii)
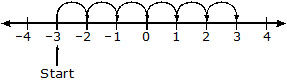
Moving 6 numbers to the right of – 3, we reach the point 3.
EXAMPLE. Write all integers between
(i) – 2 and 3 (ii) – 4 and 2
Sol.
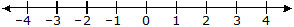
(i) The integers between – 2 and 3 are – 1, 0, 1, 2.
(ii) The integers between – 4 and 2 are – 3, – 2, – 1, 0, 1.
ABSOLUTE VALUE OF INTEGERS
On the number line, the distance from, say, 0 to +5 is said to be 5 units. So, the absolute value of 5 is 5. Also, the distance, from 0 to – 5 is 5 units. So, the absolute value of –5 is 5.
The absolute value of an integer is the distance of that integer from 0 irrespective of the direction, i.e. negative or positive.
The absolute value of 3 is written as | 3 | which is read as absolute value of 3 and is equal to 3.
The absolute value of – 3 is written as | – 3 | and is read as absolute value of – 3 and is equal to 3.
EXAMPLE. State the absolute values of the following.
(a) | – 82 | (b) | 121 |
Sol. (a) | – 82 | = 82
(b) | 121 | = 121
The two integers are called additive inverse of each other if their sum is zero. So, –5 is the. additive inverse of 5 and 7 is the additive inverse of – 7.
OPERATION ON INTEGERS
Addition
Rules for addition of integers
1.When adding integers with like signs (both positive or both negative), add their absolute values, and place the common sign before the sum.
2. When adding integers of unlike signs, find the difference of their absolute values and give the result the sign of the integer with the larger absolute value.
3. When the addition and subtraction signs are placed side by side without any number in between, these two opposite signs give a negative sign.
For EXAMPLE
– 3 + (– 7) = – 3 – 7 = – 10
4. A number when added to its opposite gives zero as the result.
EXAMPLE. Add the following
(a) 2 + 3 (b) 2 + (– 3) (c) – 2 + 3 (d) – 2 + (– 3)
Sol. (a) 2 + 3 = (+ 2) + (+ 3) = 5
(b) 2 + (– 3) = – 3 + 2 = – 1
(Find the difference of the absolute values and since 3 is greater than 2 and it has a negative sign, the answer will be – 1.)
(c) – 2 + 3 = + (3 – 2) = + 1
(Find 3 – 2 and since 3 > 2 and it is a positive integer, the answer will also be positive.)
(d) (– 2) + (– 3) = – 2 – 3 = – 5
(Add the absolute values and place the common sign which is negative or minus sign in the answer.)
Subtraction
We know that subtraction is the reverse of addition.
EXAMPLE. Consider 5 – 3. Actually we have to subtract + 3 from 5.
So, we need to find a number which when added to 3 gives 5.
The answer 2, i.e., 5 – 3 = 5 + (– 3) = 2
Subtraction is the opposite of addition. We can change subtraction to addition by adding the additive inverse of the second number to the first number.
EXAMPLE. Find 6 – (– 7)
The additive inverse of – 7 is 7.
So, 6 – (– 7) = 6 + (+ 7) = 6 + 7 = 13
EXAMPLE. Find – 13 – (+ 5)
The additive inverse of + 5 is – 5
So, – 13 – (+ 5) = (– 13) + (– 5)
= – (13 + 5) = – 18
EXAMPLE. Subtract the sum of 998 and – 486 from the sum of – 290 and 732.
Sol. Sum of 998 and – 486 is 998 + (– 486)
= (998 – 486) = 512
Sum of – 290 and 732 is – 290 + 732
= 732 – 290 = 442
Now, 442 – 512 = 442 + (– 512) = – 70
[We subtract 442 from 512 and give minus sign to the result]
EXAMPLE. The sum of two integers is – 396. If one of them is 64, determine the other.
Sol. Other integer = Sum – Given integer
= (– 396) – 64 = (– 396) + (– 64)
= – 460.
EXAMPLE. Replace * by < or > in each of the following to make a true statement.
(i) – (6) + (– 9) * (– 6) – (– 9)
(ii) (– 12) – (– 12) * (– 12) + (– 12)
Sol. (i) Left side = (– 6) + (– 9) = – 15,
Right side = (– 6) – (– 9)
= (– 6) + 9 = 3
Since – 15 < 3 so the answer is <
(ii) Left side = (– 12) – (– 12)
= (– 12) + 12 = 0
Right side = (– 12) + (– 12) = – 24
Since 0 > – 24 so the answer is >.
EXAMPLE. Find the value of – 12 – [(– 15) + (– 2) – 3].
Sol. – 12 – [(– 15) + (– 2) – 3]
= – 12 – [(– 15) + (– 2) + (– 3)]
= – 12 – (– 20) = – 12 + 20 = 8.
EXAMPLE. On a particular day, the temperature at Deheradun at 10 AM was 20ºC but by midnight, it fell down to 11ºC. The temperature at Bangaluru at 10 AM the same by was 30º C but fell down to 18º C by the midnight.
Which fall is greater?
Sol. Fall in temperature at Dehradun
= 20ºC – 11ºC = 9ºC
Fall in temperature at Bangaluru
= 30ºC – 18ºC = 12ºC
\ The fall in temperature at Bangaluru is greater and is 12ºC
Points to Remember
1. The smallest positive integer is 1.
2. The greatest negative integer is – 1.
3. There is no greatest positive integer and smallest negative integer.
4. The integer on the right is always greater than the one on the left.
5. For every positive integer, there exists a negative integer at the same distance from zero in the opposite direction. These two integers are called the opposites of each other. These two integers are also called additive inverse of each other as their sum is zero.
6. The absolute value of a negative or a positive integer is the positive value of the integer as it represents the distance of the number from zero.

