The English word Geometry has been derived from the Greek woud geometron which means to measure the Earth'. Geometrical idea have developed over centuries to cater to needs in art, architecture etc. Here, we will discuss some basic concepts in geometry.
POINT
A point shows an exact location of an object. It is the basic unit of geometry. It is represented with the help of a dot. It is named by using a single capital English alphabet.
LINE, LINE SEGEMENT, AND RAY
A line is a collection of points going endlessly in both directions along a straight path.
The symbol for a line is «.
The arrows show that line goes on endlessly in both directions. A and B are two points on the line.
We call it line AB and write it as or . It can also be named by means of any small English letter, say l.
(a) Intersecting Lines :
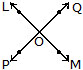
If two or more lines meet each other at one point then they are called intersecting lines. Two intersecting lines have one common point.
(b) Parallel Lines :
If two or more lines do not meet each other however far they are extended, then they are called parallel lines.
The opposite edges of a book, table, ruler etc. are good examples of parallel lines.
(c) Line segment :
A line segment is part of a line. It has two endpoints and has a fixed legnth.
We name the segment by its endpoints.
The symbol for a line segment is "_____" .
Points P and Q are the two endpoints of the line segment PQ as shows above. We write it as or .
(d) Ray :
You must have noticed rays of light coming out of a torch or car headlights. A ray is part of a line. It has one endpoint and goes on endlessly in one direction. The endpoint is mentioned first while naming a ray.
Ray QR is written as . It is important to note that is not a ray as Q is an end point.
(e) Collinear Points:
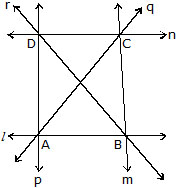
Three or more points in a plane are said to be collinear if they all lie on the same line.
In Fig. points A, B, C and D are collinear because only one line l passes through all of them.
If the points do not lie on a line, they are called non-collinear points.
NOTE :
We have learnt earlier that through two given distinct points, we can always draw a line.
Thus two distinct points are always collinear. But given three distinct points may or may not be collinear. So we talk of collinearity of three or more distinct points.
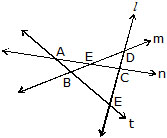
Ex. In Fig. name :
(i) Four non-collinear points.
(ii) Point of intersection of the lines l and m.
(iii) Point of intersection of the lines r and n.
(iv) Point of intersection of the lines q and n.
(v) Point of intersection of the lines p and q.
(vi) Four line segments.
Sol. (i) A, B, C, D
(ii) B
(iii) D
(iv) C
(v) A
(vi) , , ,
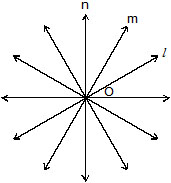
(f) Concurrent lines
Three or more lines in plane are said to be concurrent if they all pass through the same point. In below Fig., the lines l, m, n,..... all pass through a common point O. Such lines are said to be concurrent lines and we say that they are concurrent at O. The point O is called the point of concurrency.
The point of concurrency of three or more lines in a plane is also called the point of intersection of these given lines.
Now look at below Fig., the lines l, m, n, t are not concurrent lines but are intersecting lines. The points A, B, C, .... are the points of intersection on the lines l, m, n,... but none of them is a point of concurrency. ln this case the point of intersection is not point of concurrency.
NOTE :
As collinearity is defined for three or more points, we define concurrency for three or more lines.
Curves
When you draw lines on a piece of paper without lifting the pencil and without using a scale, the shapes that you get are called curves. Some examples are shown below.
Simple curve : A curve that does not cross itself is called a simple curve. The figures shown below are simple curves.
Open and Closed figures
Open figure : The figures that do not begin and end at the same point are called open figures.
Closed figure : The figures that begin and end at the same point are called closed figures. They are also called closed curves. The closed curves that do not cross themselves are called simple closed curve. For example : triangle, circle, ellipse, rectangle, square, etc. are all closed figures.
POLYGON
A polygon is a closed figure made by joining three or more line segments (not curves), where each line segments intersects exactly two other line segments. For example triangle, quadrilateral, pentagon, etc., are all examples of polygon.
If all sides of a polygon are equal and all angles are also equal, then it is called a regular polygon.
Sides, vertices, and diagonals
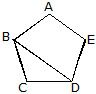
Consider the given figure. This is a polygon.
(a) The line segment forming a polygon are called its side. ln the given polygon , , , are sides.
(b) Any two sides with a common end point are called adjacent sides.
(c) The meeting point of a pair of sides is called vertex. Side and meet at B, so B is a vertex of the polygon ABCDE. Similarly A, C, D and E are the other vertices.
(d) The end points of the same side are called adjacent vertices. Vertices A and B are adjacent vertices but A and C are not.
(e) The line joining two non-adjacent vertices of a polygon is called a diagonal. Since A and C are
non-adjacent vertices, so is a diagonal.
lnterior and exterior of closed figures :
There are three parts in a closed curve
(a) lnterior (inside) of the curve.
(b) Exterior (outside) of the curve
(c) Boundary of (on) the curve.
The interior of a curve together with its boundary is called its region.
A lies in the interior of the curve, B on its boundary and C lies in its exterior.
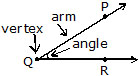
ANGLE
An angle is formed when two rays meet at a common point called a vertex. Each of these rays is called an arm of the angle. An angle is represented by the symbol Ð.
In figure and meet at the vertex Q to form an angle PQR. We write it as ÐPQR or ÐRQP or ÐQ. An angle can also be formed by the intersection of line segment.
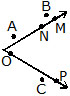
lnterior of an angle :
The space within the arms of an angle, produced indefinitely, is called the interior of the angle, ln figure points P, Q and R are said to lie in the interior of the angle.
Exterior of an angle :
The space outside the arms of an angle, produced indefinitely, is called the exterior of the angle, Point A, B, and C lie in the exterior of the angle shown in Figure.
M, N, O and P are points on the angle and are, there fore, part of the angle.
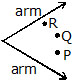
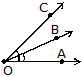
Adjacent Angles :
Two angles which have a common arm, a common vertex, and lie on either side of the common arm are called adjacent angles. ln Fig. ÐAOB and ÐBOC are adjacent angles as they have a common arm , a common vertex O and both the angles AOB and BOC are on either side of the common arm . Both the angles are distinct angles and no part of ÐAOB is a part of ÐBOC and vice versa.
TRIANGLE
A triangle is a closed figure made of three line segments. ln figure, line segments AB,BC,CA form a closed figure. The figure given below is a triangle and is denoted by ABC. This triangle can also be named as ABC, BCA, CAB, CBA, DBAC or DACB.
The line segments forming a triangle are the three sides of the triangle. In the above figure , and are the three sides of the triangle.
The point where any two of the three line segments of triangle intersect is called the vertex of the triangle. A triangle has three vertices. In the given figure, A, B and C are the three vertices.
When two lines segments intersect, they form an angle at the point. In the above triangle and intersect at B and form an angle at that vertex. This angle at B is read as ÐB or ÐABC or ÐCBA.
Thus a triangle has three angles, DABC has three angles namely ÐA, ÐB and ÐC.
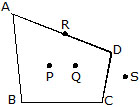
Look at DABC in figure below points P and Q are in the interior of DABC. The region within the boundary of DABC is called interior region of the triangle.
Note that DABC only refers to the boundary of the figure and not its interior. Points X, Y and Z are on n n the boundary of the DABC and hence they are on DABC. The interior region with the boundary is known as the triangular region. Points K, L and M are on the exterior of DABC.
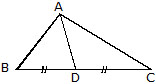
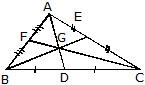
Medians of a Triangle :
A line segment joining a vertex to the mid-point of the side opposite to the vertex is called a median of the triangle.
Thus, in the above figure, D is the mid-point of BC and AD is a median. Obviously, every triangle has three medians, one from each vertex.
The point G where all the median of triangle intersects is known as Centroid.
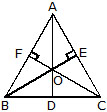
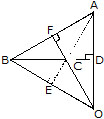
Altitudes of a Triangle :
An altitude of a triangle is the perpendicular drawn from a vertex to the opposite side (produced if necessary).
Clearly, every triangle has three altitudes, one from each vertex.
If we take BC as the base, then AD is called the height of the triangle.
The point O where all the altitudes of a triangle meets is known as Orthocentre.
QUADRILATERAL
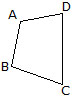
A quadrilateral is a closed figure formed by four line segments.
All the shapes shown above are quadrilaterals as they are all bounded by four line segments.
A quadrilateral has four sides, four vertices, and four angles. In the above figure , , and constitute the sides, and ÐA, ÐB, ÐC and ÐD are the four angles. These quadrilaterals are read as quadrilateral ABCD.
Elements of a Quadrilateral :
Adjacent sides : In the quadrilaterial PQRS there are four sides, namely , , and .
The two sides of a quadrilateral having a common endpoint are called adjacent sides. Thus, sides and are adjacent sides having the common endpoint Q. Sides and are also adjacent sides having the common endpoint R. Similarly, and are adjacent sides, and and are also adjacent sides.
Opposite sides : The sides and are called opposite sides. Similarly, and are also opposite sides. They have no common end point.
Adjacent angles : Two angles of a quadrilateral which have a common arm are called adjacent angles.
Therefore ÐP and ÐQ are adjacent angles as they have a common arm . Similarly, ÐQ and ÐR ; ÐR and ÐS ; ÐS and ÐP are also adjacent angles.
Opposite angles : ÐP and ÐR are opposite angles as they have no common arm.
Similarly, ÐQ and ÐS are also opposite angles.
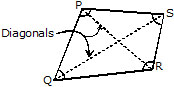
Diagonals : The line segments joining the opposite vertices are called the diagonals of the
quadrilateral. and are the two diagonals of the quadrilateral PQRS.
lnterior and exterior of a quadrilaterial :
The region inside the quadrilateral ABCD is called its interior and that outside is called the exterior. ln the given figure, four points P, Q, R and S are marked. P and Q are said to be in the interior of the quadrilateral ABCD, R is on the quadilateral ABCD, while S is in the exterior of the quadrilateral ABCD.
The interior of the quadrilateral ABCD along with the quadrilateral ABCD is called the quadrilateral region of ABCD, i.e., P, Q and R are points in the quadrilateral region of the quadrilateral is 360º.
CRICLE
A circle is a simple closed curve all of whose points are at the same distance from a given point O in the same plane. The given point O is called the the centre of the circle.
Parts of a Circle
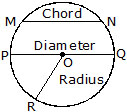
A line segment joining any two points on a circle is called a chord of that circle.
A chord that passes through the centre of a circle is called a diameter of that circle.
NOTE :
(i) A diameter is the longest chord of a circle.
(ii) The diameter is twice the radius i.e. PQ = 2OR
(iii) The distance around a circle is called the circumference.
A Few More Definitions
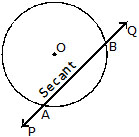
1. Secant. A line which intersects or meets the circle at two distinct points is called a secant.
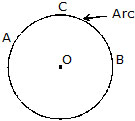
2. Arc. A part (continuous) of a circle is called an arc.
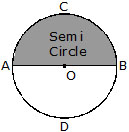
3. Semi-circle. A diameter divides a circle into two equal parts which are called semi-circles.
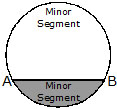
4. Segment. A chord AB of a circle divides the area enclosed by it into two parts which are called segments.
The smaller part is called a minor segment and the larger part a major segment. The chord also divides the circumference of the circle into two parts. The smaller part is called a minor arc because it is less than a semicircle and the larger part a major arc because it is greater than a semi-circle.
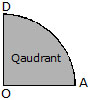
5. Sector and Quadrant. The part of a circle enclosed by any two radii of the circle is called a sector of the circle.
In this figure OACB is a sector.
If the two radii are at right angles to each other the sector is called a quadrant. A quadrant is thus th of a circle. In the figure AOD is a quadrant.
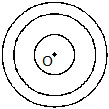
6. Concentric Circles : Two or more circles drawn with the same centre are called concentric circles.
OBJECTIVE TYPE
Q.1 Which of the following figures is made of line segments only?
(A) (B)
(B)  (C)
(C) (D)
(D) 
Q.2 Which of the following is another name for ÐABC?
(A) ÐA (B) ÐCBA (C) ÐACB (D) ÐCAB
Q.3 Which of the following rays are the arms of ÐBOA?
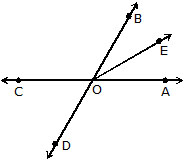
(A) OB, OE (B) OE, OA (C) OB, OA (D) OC, OA
Q.4 Which of the following is not a pair of adjacent angles of quadrilateral ABCD ?
(A) ÐA, ÐB (B) ÐC, ÐD (C) ÐB, ÐD (D) ÐD, ÐA
Q.5 A quadrilateral has
(A) 2 diagonals, 3 angles (B) 4 diagonals, 4 angles
(C) 2 diagonals, 4 angles (D) 4 diagonals, 4 sides
Q.6 The complete distance around a circle is called the
(A) Secter (B) Quadrant (C) Circumference (D) Segment
Q.7 One-fourth part of a circle is known as a
(A) semi-circle (B) major segment (C) sector (D) quadrant
Q.8 The longest chord of a circle is known as a
(A) radius (B) diameter (C) circumference (D) secant
Q.9 An arc is a continuous part of the _______ of the circle.
(A) diameter (B) major segment (C) circumference (D) chord
Q.10 The centre of the circle always lies in the interior of the
(A) minor segment (B) semi-circle (C) major segment (D) plane
Q.11 An exact location in space is called a
(A) ray (B) point (C) line segment (D) plane
Q.12 Which of the following has no end points ?
(A) (B) (C) (D)
Q.13 a quadrilateral is a simple closed figure formed by ________ line segments.
(A) 3 (B) 4 (C) 2 (D) 5
Q.14 The radius of a circle is 3 cm. Its diameter is
(A) 1.5 cm (B) 9 cm (C) 4.5 cm (D) 6 cm
Q.15 The end points of a diameter of a circle divide the circle into two parts, each of which is known as
(A) segment (B) sector (C) semi-circle (D) quadrant
Q.16 What is three or more lines called if they pass through a common point ?
(A) parallel lines (B) intersecting lines (C) concurrent (D) none of these
Q.17 How many end points does a ray has ?
(A) one (B) two (C) three (D) zero
Q.18 Two angles of a quadrilateral having a common side are called :
(A) opposite angles (B) equal angles (C) adjacent angles (D) none of these
Q.19 The point where a pair of adjacent sides of a polygon meets is called :
(A) diagonal (B) adjacent angles (C) vertex (D) none of these
Q.20 Diameter =
(A) 2 × radius (B) 2 (C) radius (D) 1/2 × radius
SUBJECTIVE TYPE
Q.1 Write :
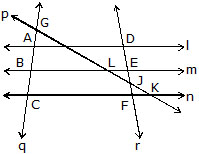
(i) All pairs of parallel lines.
(ii) All pairs of intersecting lines.
(iii) Lines whose points of intersection is L.
Q.2
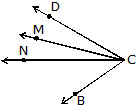
Name the six angles in the diagram above that have C as a vertex.
Q.3 In Fig. name the lines which are concurrent at the point
(i) A (ii) O (iii) B
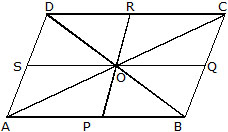
Name also the sets of collinear points.
Q.4 In the given triangle, S is mid point of QR :
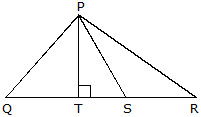
(i) The side opposite to vertex P, in DPQR.
(ii) The altitude from vertex P, in DPQR.
(iii) The angle opposite to side PQ, in DPQT.
(iv) The vertex opposite to side PR in DPQR.
(v) The median from vertex P, in DPQR.
Q.5 Two points A and B are given. How many circles can be drawn
(i) passing through both the points ?
(ii) with A as centre and AB as radius ?
Q.6 O is the centre of the two circles in the figure drawn below. Fill up the blanks in the following :
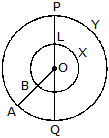
(i) _______ are radii of the inner circle.
(ii) OA, OQ, OP are the ________ of the ________ circle.
(iii) LM is a ________ of the ________ circle.
(iv) PQ is a ________ of the ________ circle.
(v) The two circles are called ________ circles.
(vi) LXM is a ________ of the ________ circle.
(vii) POA is a _________ of the _________ circle.
Q.7 Answer True (T) or False (F) :
(i) Only one ray can be drawn with a given initial point.
(ii) Two planes intersect in a line.
(iii) The interior of a triangle, and the triangle itself make the triangular region.
(iv) In a quadrilateral PQRS, P and R are a pair of adjacent angles.
(v) The line segments joining the centre of the circle and any point on the circle are all equal.
(vi) A segement is a figure enclosed by a chord and the corresponding arc of the circle.
(vii) The distance of a point which is in the interior of a circle from the centre, is less than its radius.
(viii) Two concentric circle have two distinct centres.
Q.8 Name the doted/shaded part.
(i)

(ii)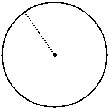
(iii) 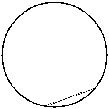
(iv)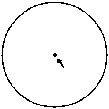
(v)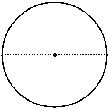
(vi) 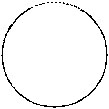
(vii)
(viii) 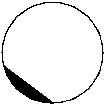
Q.9 In a quadrilateral, define each of the following :
(i) Sides (ii) Vertices (iii) Angle
(iv) Diagonals (v) Adjacent sides (vi) Adjacent angles
(vii) Opposite angles (viii) Opposite sides
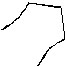
Q.10 Classify the following as open or closed :
(i)

(ii)

(iii)

(iv)

(v)
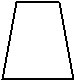
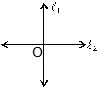

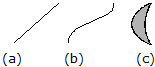
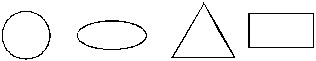



.JPG)
(B)

(D)

