Thrust : Force acting normally on a surface is called the thrust.
Thrust is a vector quantity and is measured in the unit of force, i.e., newton (N).
Pressure : The thrust acting on unit area of the surface is called the pressure.
If a thrust F acts on a area A, then pressure (P) =
Pressure is directly proportional to the force.
Pressure in inversely proportional to the area.
For the examples :
Ex. A sharp knife cuts easily than a blunt knife by applying the same force.
Ex. A sharp needle pressed against our skin pierces it. But a blunt object with a wider contact area does not affect the skin when pressed against it with the same force.
1. The foundation of a building or a dam has a large surface area so that the pressure exerted by it on the ground is less.
This is done to prevent the sinking of the building or the dam into the ground.
2. The tyres of a bus or a truck have larger width than those of a car. Further, the number of tyres of heavy vehicles is more than four.
This is done to enable the tyres to carry more weight and to
prevent sinking into ground.
3. A sleeping mattress is so designed that when you lie on it, a large area of your body comes in its contact. This reduces the pressure on the body and sleeping becomes comfortable.
4. Railway track are laid on large sized wooden or iron sleepers.
We know, Pressure =
The weight (i.e., thrust) of the train is spread over a large area of the sleepers. Therefore, the pressure acting on the ground under the sleepers is reduced. This prevents the sinking of the ground under the weight of the train.
5 A sharp knife is more effective in cutting the objects than a blunt knife.
The pressure exerted =
The area under the sharp knife is less than the area under the blunt knife. Hence, the pressure exerted by the sharp knife is more than the pressure exerted by the blunt knife on an object. Therefore, the sharp knife penetrates easily into the object than the blunt knife when same force is applied in both the cases. Hence, a sharp knife cuts the objects easily than a blunt knife.
6. A camel walks easily on the sandy surface than a man inspite of the fact that a camel is much heavier than a man.
This is because the area of camel's feet is large as compared to the area of man's feet. So the pressure exerted by camel on the sandy surface is very small as compared to the pressure exerted by man. Due to large pressure, sand under the feet of a man yields (i.e. sink) and hence he cannot walk easily on the sandy surface.
7. A sharp needle, pierce the skin easily but not a blunt needle although the force applied on both the needles is same.
Pressure exerted =
The area under the pointed end of the sharp needle is very small as compared to the area under the pointed end of the blunt needle. So pressure exerted by the sharp needle is much more than the pressure exerted by the blunt needle. Hence a sharp needle pierces the skin easily than the blunt needle.
8. It is painful to hold a heavy bag having strap made of a strong and thin string.
We know, Pressure =
When we hold a heavy bag having strap made of a strong and thin string, then the area under the strap is small. Hence, large pressure is exerted by the strap on our fingers or shoulder. Due to this large pressure, the strap tends to cut the skin and hence pain is caused.
9 The army tank has a large weight. Therefore to avoid large pressure on the ground its weight is distributed throughout the tank. This is done by making the tank run on a steel track rather than on wheels. The steel tracks reduce the
pressure of the ground .
The SI unit of pressure is called pascal (Pa) in honour of Blaise Pascal.
I Pa = 1 N/m2
One pascal is defined as the pressure exerted on a surface area of 1 m2 by a thrust of 1 N (acting normally on it).
Other units:
(i) In C.G.S unit of pressure is dyne/cm2
(ii) 1 bar = 105 N/m2
(iii) 1 millibar = 102 N/m2
(iv) 1 atmospheric pressure (1 atm) = 101·3 k Pa = 1·013 bar = 1013 m bar = 760 mm of Hg
(v) 1 Torr = 1mm of Hg
(i) Pressure exerted by the liquid is the same in all directions about a points
(ii) Pressure exerted is the same at all points in a horizontal plane as well as in a stationary liquid.
(iii) Pressure at a points inside a liquid increases with depth from the free surface.
(iv) Pressure at a particular depth is different for different liquids, i.e. P = hdg
where, h = height of the column of liquid. d = density of the liquid
g = acceleration due to gravity
(v) The pressure exerted anywhere in a confined liquid is transmitted equally and undiminished in all directions throughout the liquid which is called 'Pascal's law'.
(A) Hydrostatic Pressure :
The normal force (or thrust) exerted by a liquid at rest per unit area of the surface in contact with it is called "pressure of liquid or hydrostatic pressure."
(B) Atmospheric Pressure :
The pressure exerted by atmosphere is called atmospheric pressure.
(i) At sea level, atmospheric pressure is the pressure exerted by 0.76 m of mercury column i.e. h = 0.76 m.
(ii) The density of mercury,
d = 13.6 × 103 kg m–3 and g = 9.8 ms–2.
Þ atm pressure = P = hdg = 1.013 × 105 Nm–2 or Pa
Density of a substance is defined as its mass per unit volume.
density(d) =
Unit of density :- Since mass (M) is measured in kilogram (kg) and the volume (V) is measured in metre3 (m3), the unit of density is kg/m3. In cgs system, the unit of density is g cm–3.
These units are related as : 1 g cm–3 = 1000 kgm–3.
A substance which can flow is called a fluid. All liquids and gases are thus fluids. We know that a solid exerts pressure on a surface due to its weight. Similarly, a fluid exerts pressure on the container in which it is contained due to its weight. However, unlike a solid, a fluid exerts pressure in all directions.
A fluid contained in a vessel exerts pressure at all points of the vessel and in all directions.
All the streams of water reach almost the same distance in the air.
In an enclosed fluid, if pressure is changed in any part of the fluid, then this change of pressure is transmitted undiminished to all the other parts of the fluid.
When a body is partially or wholly immersed in a liquid, an upward force acts on it which is called upthrust or buoyant force. The property of the liquids responsible for this force is called buoyancy.
Buoyancy is a familiar phenomenon : a body immersed in water seems to weigh less than when it is in air. When the body is less dense than the fluid, then it floats. The human body usually floats in water, and a helium filled balloon floats in air.
When a body is immersed in a fluid (liquid or gas) it exerts an upward force on the body. This upward force is called upthrust or buoyant force (U or FB) and the phenomenon is termed as buoyancy. Thus buoyancy or upthrust is the upward force exerted by a fluid (liquid or gas) when a body is immersed in it.
It is a common experience that when a piece of cork is placed in water it floats with two-fifth of its volume inside water. If the cork piece is pushed into water and released it comes to the surface as if it has been pushed by someone from inside due to the buoyant force exerted by fluid.
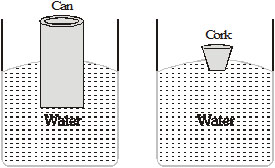
Upthrust depends upon the following two factors :
(a) The volume of the body submerged in the fluid. :- It is found that greater the volume of a body greater is the upthrust it experience when inside a fluid.
(b) The density of fluid in which the body is immersed :- It is also found that greater the density of the fluid greater is the upthrust it applies on the body.
Archimedes principle states that :- "Anybody completely or partially submerged in a fluid is buoyant up by a force equal to the weight of the fluid displaced by the liquid".
In other words :- "When a body is partially or completely immersed in a fluid, the fluid exerts an upward force on the body equal to the weight of the fluid displaced by the body.
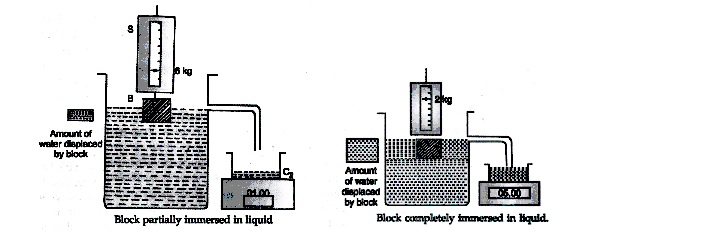
Consider a container C1 filled with water upto the level from where pipe P extends out. The other end of pipe P opens to a small container C2 placed on a weighing balance which measure 00.00 [after the placement of the container C2]. A block B hangs on a spring balance S which shows a reading of 7 kg.
(a) If we partially immerse the block in water we observe some water flows out from C1 to C2 through P. The weighing machine shows a reading 1 kg and the loss of reading in spring balance is 7 – 6 = 1kg. This means that weight of water displaced by the block is equal to loss in weight of block.
(b) Now we completely immerse the block in water, we observe that the weight of water displaced by the block is 5 kg and the reading in spring balance is 2 kg. The loss of weight of block is 7 – 2 = 5 kg. Again we reach the same conclusion that weight of water displaced by the block is equal to the loss in weight of block.
(c) What happens when the block is further immersed? No more water will be displaced by the block and therefore
reading shown by weighing machine and spring balance remains
unchanged.
Why the spring balance shows a loss in weight of the block when Fig. A block of 7 kg hanging on a the block is immersed in water? This is because of buoyant force on spring balance acting vertically upwards. The loss in weight is equal to the buoyant force.
Buoyant force µ volume of liquid displaced (V). If two bodies of different material have same volume, the buoyant force acting on them, when completely immersed in water, is same.
Instead of water if we take a liquid lighter than water then the volume displaced by the block on complete immersion will be the same but the buoyant force will be less. This is because the density of lighter liquid is less than that of water.
We know that Density =
\ Mass = Density × Volume
For lighter liquids, the mass of the liquid displaced is less even when the volume displaced is the same.
Buoyant force & Density of liquid
i.e., Buoyant force µ d
It has also been found that buoyant force also depends on the acceleration due to gravity.
Buoyant force µ g
If we combine all the three, we get
Buoyant force µ V dg
Þ Buoyant force µ mg [mass = V × d]
Þ Buoyant force µ Weight of the liquid displaced
Note: A body placed in a gaseous medium is also acted by the upthrust equal to the weight of the gas displaced.
The above facts has been summarised in Archimedes principle which states that the upward force acting on a solid body which is partially or completely immersed in a fluid, is equal to the weight of the fluid displaced.
This upward force is called buoyant force or upthrust.
Relative density (R.D.) of a substance is the ratio of the density of the substance to the density of water at 4°C.
Thus,
Relative density =
Unit of Relative Density
Since relative density is a ratio of two similar quantities, it has no unit.
Further,


Relative density for solids and liquids can also be determined with the help of Archimedes principle.
(i) For solids:
By definition, we have
Relative density =
=
Relative density =
Relative density of a solid can be measured by weighing it first in air and then when fully immersed in water
Let weight of the body in air = W1
Weight of solid body in water = W2
Loss in weight = W1 – W2
R.D. = =
(ii) For liquids:
To measure relative density of a liquid, choose a body which can be fully immersed in water as well as in the given liquid. The body is weighed first in air, then fully immersed in water and then fully immersed in that particular liquid.
R.D. =
=

Relative density of a substance is a number of times the given substance is heavier than the equal volume of water. When we say that the relative density of silver = 10.5, it means, silver is 10.5 times heavier than equal volume of water.
Law of floatation is an extension of Archimedes principle.
When a body is partially or fully immersed in a fluid, then following vertical forces are experienced by it.
(a) Its weight (W) acting vertically downwards through the centre of the body.
(b) Force of buoyancy (B or FB) or upthrust, acting vertically upwards through the centre of gravity of the body.
The following three cases arise :-
(1) When W < B, the body floats : In this case the body will rise above the surface on the liquid to the extent that the weight of the liquid displaced by its immersed part equals the weight of the body. Then the body will float with only a part of it immersed in the liquid. In this case Vrg < Vsg or r < s. Thus if a cork, which has a density less than that of water will rise in water till a portion of it is above water. Similarly a ship floats in water since its density is less than the density of water.
(2)

(3) When W = B :- The resultant force acting on the body when fully immersed in the fluid is zero. The body is at rest anywhere within the fluid. The apparent weight of the body is zero for all such positions.
Thus, we find that a body will float when its weight is equal to the weight B of the fluid displaced i.e. the upthrust.
(a) Special features of floating body:
(i) Floating body is a weightless body: As the weight acting downwards is neutralized by the buoyant force acting upwards, a floating body is a weightless body. We can also say that the apparent weight of the floating body is zero.
(ii) Loss of weight of a floating body is complete: As the floating body is weightless, it means it has lost its weight completely.
loss of weight for a floating body
= Real weight – Apparent weight
= Real weight – 0 = Real weight
(b) Relation between Density of Solid and Liquid:
Let r1 be the density of the solid whose volume is V1. Let r2 be the density of the liquid and the volume of the portion of the solid immersed in the liquid be V2.
Now, weight of the floating solid = weight of the liquid displaced.
i.e. V1r1g = V2r2g \
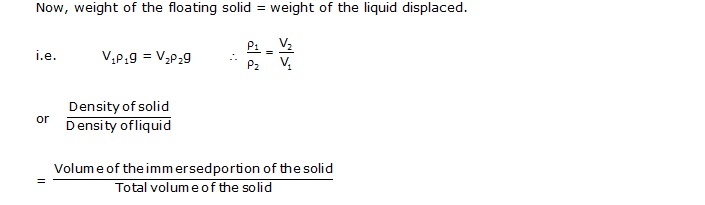
Q. The volume of a solid of mass 500 g is 350 cm3.
(A) What will be the density of this solid?
(B) What will be the relative density of solid?
(C) Will it float or sink in water?
(D) What will be the mass of water displaced by this solid?

Thus the relative density of solid is 1.42.
(C) Since the relative density of this solid (1.42) is greater than the relative density of water which is 1 so it will sink in the water.
(D) The solid will displace water equal to its own volume. Since the volume of solid is 350 cm3 so it will displace 350 cm3 of water. Now, volume of water displaced is 350 cm3 and the density of water in common units is 1 gm/cm3. Putting these values in (i), we get,
Density of water =
We get 1 gm/cm3 =
So, Mass of water = 1 g/cm3 × 350 cm3
Thus, the mass of water displaced is 350 grams.
From law of floatation, we know that a body will float in a liquid when its weight W is equal to the weight w of the liquid displaced by the immersed part of the body. But this does not necessarily indicate that the body will be in equilibrium. A body will be in equilibrium only if the resultant of all the forces and couples acting on the body is zero. If W and w act along different lines, they will then form a couple which will tend to rotate the body. Thus, a floating body can be in equilibrium if no couple acts on it. It will be so if the line of action of W and w is along the same vertical straight line. Thus, there will be equilibrium of floating bodies if the following conditions are fulfilled:
(i) A body can float if the weight of the liquid displaced by the immersed part of body must be equal to the weight of the body.
(ii) A body can be in equilibrium if the centre of gravity of the body and centre of buoyancy must be along the same vertical line.
(iii) The body will be in stable equilibrium if centre of gravity of body lies vertically below the centre of buoyancy and in the unstable equilibrium if centre of gravity lies vertically above the centre of buoyancy.
² NOTE:
When an ice block is floating in water in a vessel, then the level of water in the vessel will not change when the whole ice melts into water.
When an ice block is floating in a liquid in a vessel and ice completely melts, then the following cases may arise for the level of liquid in the vessel.

Q. A body of volume 300 cm3 and relative density 1/3 is placed in water. Will it sink or float in water and what will be the volume of water displaced by it?
Sol. Relative density of body =
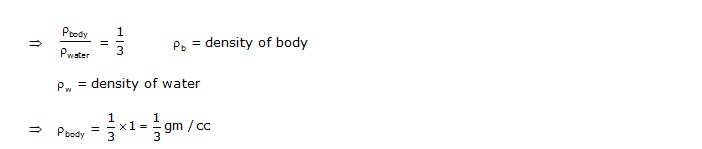
Since density of body is less then density of water it will float.
Let “x” be the volume of body immersed inside the water then volume of displaced water will also be equal to “x”.
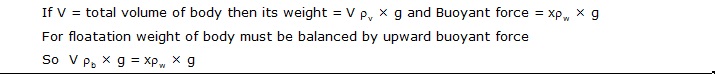

1. In designing ships and submarines.
2. Lactometer is based on the Archimedes principle. It is used to determine the purity of a sample of milk.
3. Hydrometer is also based on the Archimedes principle. It is used to determine the density of liquids.
(a) Ships :
Although it is made of iron and steel which are materials denser than water a ship floats in water. This is due to the fact that a floating ship displaces a weight of water equal to its own weight including that of the cargo. The volume of the ship is much larger than the volume of the material with which it is made. Since the empty space in the ship contains air therefore its average density is less than the density of water. Thus a ship floats with a small section under water.
A ship has to move in waters of different seas which have different densities. As a result it sinks more in water with less density than in water with more density. Therefore ships are marked with white lines on its sides called load lines of pimsoll marks. The load lines (called the Plimsoll Mark) on the side of a ship of a ship show how low in the water it can lie and still be safely and legally loaded under different conditions.
A submarine, figure sinks by taking water into its buoyancy tanks. Once submerged, the upthrust is unchanged but the weight of the submarine increases with the inflow of water and it sinks faster. To surface, compressed air is used to blow the water out of the tanks.
Each submarine is provided with ballast tanks. If the submarine has to submerge these tanks are filled with water. This makes the average density of the submarine greater than that of water as a result it sinks. When the submarine has to be surfaced, compressed air is blown into these tanks to expel the water. Again the average density of the submarine becomes less than that of water, hence it floats.
Ex.1 A sealed tin of Coca-cola of 400 g has a volume of 300 cm3. Calculate the density of the tin.
Sol. Here, mass of tin m, = 400 g
Volume of tin, V = 300 cm3
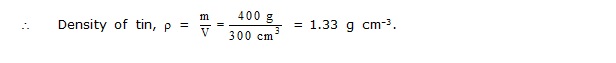
Ex.2 A sealed cane of mass 600 g has a volume of 500 cm3. Will this cane sink in water ? Density of water is 1 g cm–3.
Sol. Here, mass of cane, m = 600 g
Volume of cane, V = 500 cm3
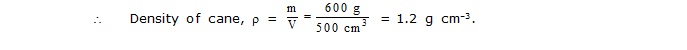
Since, density of the cane is greater than the density of water, so the can will sink in water.
Ex.3 The density of water is 1000 kg m–3. If density of gold is 19320 kg m–3, find the relative density of the gold.
Sol. Density of water = 1000 kg m–3
Density of gold = 19320 kg m–3
Using, R.D. of gold = Density of gold/Density of water
we get R.D. of gold = 19320 kg m-3/ 19320 kg m-3 = 19.32
Ex.4 The density of water is 1000 kg m–3. If relative density of iron is 7.874, then calculate the density of iron.
Sol. Density of water = 1000 kg m–3
Relative density (R.D.) of iron = 7.874
Using, R.D. of iron = Density of iron / Density of water , we get
Density of iron = R.D. of iron × density of water
= 7.874 × 1000 kg m–3 = 7874 kg m–3.
Ex.5 A plastic bottle of 500 g has a volume of 450 cm3. Will the bottle float or sink in water ? Density of water is 1 g cm–3 ? Also calculate the mass of the water displaced by the bottle.
Sol. Mass, m = 500 g
Volume, V = 450 cm3
![]()
Since, density of bottle is greater than the density of water (1 g cm–3), so the bottle will sink in water.
(ii) Mass of water displaced by the bottle = Volume of water displaced × Density of water
= Volume of bottle × Density of water
= 450 cm3 × 1 g cm–3
= 450 g.
Ex.6 Fig. (a) shows how to calculate pressure exerted by a brick of mass 3 kg : (a) when standing on end; (b) when lying flat. The total force or thrust exerted is the same in both the cases.
Sol. In Fig. (a), A1 = 5 cm × 10 cm = 50 cm2 = 50 × 10–4 m2 and
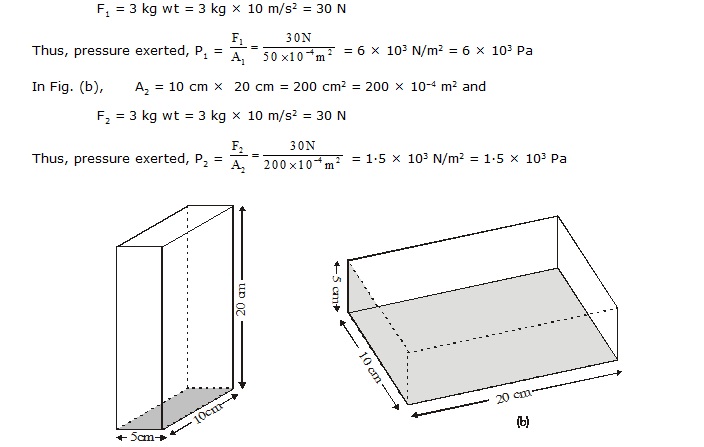
Q.1 Why is it difficult to hold a school bag having a strap made of a thin and strong string?
Ans. It is difficult to hold a school bag having a thin strap because the pressure on the shoulders is quite large. This is because the pressure is inversely proportional to the area on which the force acts. The smaller is the area the larger will be the pressure on the surface. In the case of a thin strap, the contact area is very small. Hence, the pressure exerted on the shoulder is very large.
Q.2 What do you mean by buoyancy?
Ans. The tendency for an immersed body to be lifted up in a fluid, due to an upward force that acts opposite to the action of gravity is called buoyancy.
Q.3 Why does an object float or sink when placed on the surface of water?
Ans. If the density of an object is more than the density of the liquid, then it sinks in the liquids. This is because the buoyant force acting on the object is less than the weight of the object. If the density of the object is less than or equal to the density of the liquid, then it floats on the surface of the liquid. This is because the buoyant force acting on the object is equal to the weight of the object.
Q.4 You find your mass to be 42 kg on a weighing machine. Is your mass more or less than 42 kg?
Ans. When you weigh your body, an upward buoyant force acts on your body due to the air (a fluid) present around you. As a result, the body gets pushed slightly upwards, causing the weighing machine to show a reading slightly less than the actual value.
Q.5 You have a bag of cotton and an iron bar, each indicating a mass of 100 kg when measured on a weighing machine. In reality, one is heavier than other. Can you say which one is heavier and why?
Ans. A weighing machine measures the apparent weight of an object. We know that apparent weight (Wa) is equal to true weight (Wt) minus buoyant force (FB) i.e.,
Wa = Wt – FB or Wt = Wa + FB
Now, buoyant force on the cotton due to the air present around it is large as compared to the buoyant force on the iron. This is because the volume of cotton is very large as compared to the volume of iron. As a result, the true weight of cotton must be greater than the true weight of iron. Thus, the given cotton sample is heavier than the given iron sample.
Q.6 In what direction does the buoyant force on an object immersed in a liquid act?
Ans. An object immersed in a liquid experiences a buoyant force in upward direction.
Q.7 Why does a block of plastic released under water come up to the surface of water?
Ans. Density of plastic block is less than the density of water. Thus, when it floats, it is partially immersed in water such that its weight gets balanced with the buoyant force acting on it. When it is put completely in water, buoyant force on it becomes more than its weight. thus, when it is released, it comes up to the surface of the water due to a net upward force acting on it.
Q.8 The volume of 50g of a substance is 20 cm3. If the density of water is 1 g cm–3, will the substance float or sink in water?
Ans. iven, mass of substance, m = 50 g;
volume, V = 20 cm3, density, r = ?
Density = = = 2.5 g cm–3
Q.9 The volume of a 500g sealed packet is 350 cm3. Will the packet flaot or sink in water if the density of water is 1 g cm–3? What will be the mass of the water displaced by this packet?
Ans. Given, mass of sealed packet, m = 500 g;
volume, V = 350 cm3; density, r = ?;
Density = = = 1.428 g cm–3
The density of the packet is more than the density of water (1g cm–3). Hence, the packet will sink in water. Thus, the volume of sealed packet (V) is equal to the volume of water displaced (Vw) as the packet is completely immersed in water.
i.e. Vw = V = 350 cm3
Now, mass of water displaced, ![]()
or mw = 1 × 350 = 350 g
Thus, the mass of water displaced by the packet is 350 g.
Q.1 Define ‘thrust’.
Q.2 What is the unit of thrust in SI ?
Q.3 Define the term ‘pressure’.
Q.4 Name the SI unit of pressure.
Q.5 Write the relationship between thrust and pressure. Thrust
Q.6 What is meant by upthrust or buoyant force?
Q.7 Define the term “buoyancy”.
Q.8 State the factors on which upthrust or buoyant force depends.
Q.9 Define density.
Q.10 Give SI unit of density.
Q.11 The density of silver is 10500 kg M–3. Explain this statement.
Q.12 Define relative density of a substance.
Q.13 Relative density of aluminium is 2.7. Explain this statement.
Q.14 The density of a solid is 7.9 g cm–3 in air. What is the density of the solid in SI unit ?
Q.15 Why is the bottom part of the foundation of a building made wider ?
Q.16 Why cutting instruments are sharpened ?
Q.17 Explain why it is difficult to push a tin can into water keeping its mouth upwards than when its mouth is kept downwards towards the water.
Q.18 A piece of ice is gently placed on the surface of water filled in glass tumbler, so the water rises to the brim. What will happen to the level of water when the ice melts ? Will the water overflow ? If not, explain with reason.
Q.19 You are provided with a hollow iron ball of volume 20 cm3, a mass of 15 g and a solid iron ball of mass 20 g. Both are placed on the surface of water contained in a large tub. Which will float ? Give reason for your answer.
Q.20 Explain the following :
(i) Icebergs floating in the sea are dangerous for the ship.
(ii) An egg sinks in fresh water but floats in a strong solution of salt.
(iii) An iron nail sinks in water but a ship made of iron floats.
(iv) A ship sinks to a great depth in river water than in sea water.
(v) It is easier for a man to swim in sea water than in river water.
(vi) A dead body floats, with its head immersed in water.
Q.21 A solid brass cylinder tied to a thread is hanging from the hook of a spring balance. The cylinder is gradually dipped into the water contained in a jar. What change do you expect in the reading of the spring balance ? Give reason for your answer.
Q.22 If a solid of the same density as that of a liquid is placed in it, what will happen to the solid ?
Q.23 A block of wood is kept on a tabletop. The mass of wooden block is 5 kg and its dimensions are 40 cm × 20 cm × 10 cm. Find the pressure exerted by the wooden block on the table top if it is made to lie on the table top with its sides of dimensions
(i) 20 cm × 10 cm and (ii) 40 cm × 20 cm.
Q.24 Relative density of silver is 10.8. The density of water is 103 kg m–3. What is the density of silver in SI unit ?
1. The total force exerted by a body perpendicular to the surface is known as thrust.
2. S.I. unit of thrust is newton (N).
3. Pressure is defined as the force acting perpendicular on unit area of the surface.
4. S.I. unit of pressure is N/m2 or pascal.
5. Pressure = Thrust / Area
6. The upward force exerted by a liquid on a body which is immersed in the liquid is known as upthrust or buoyant force.
7. The tendency of an object to float in a liquid is called buoyancy.
8. (i) Size or volume of body immersed in a liquid.
(ii) Density of the liquid in which the body is immersed.
9. Density of a body is defined as mass per unit volume.
10. S.I. unit of density is kg/m3 (kg M–3).
11. One cubic metre of silver has 10500 kg mass.
12. It is defined as the ratio of the density of the substance to the density of water.
13. Aluminium is 2.7 times heavier than the equal volume of water.
14. Density = 7.9 g cm–3 = 7.9 × 1000 kg M–3
= 7.9 × 103 kg M–3.
23. (i) 2459 Nm2 (ii) 612.5 Nm–2
24. 10.8 × 103 kg m–3
Q.2 Pressure exerted by a sharp needle on a surface is:
(A) more than the pressure exerted by blunt needle
(B) less than the pressure exerted by a blunt needle
(C) equal to the pressure exerted by a blunt needle
(D) none of these
Q.3 If a force of 10N acts on two surfaces (area in the ratio 1 : 2), then the ratio of thrusts will be:
(A) 1 : 2 (B) 2 : 1 (C) 3 : 1 (D) 1 : 1
Q.4 The height of mercury which exerts the same pressure as 20cm of water column, is equal to:
(A) 1.47 cm (B) 14.8 cm (C) 148 cm (D) None of these
Q.6 A force of 50N is applied on a nail of area 0.001 sq. cm. Then the thrust is:
(A) 50N (B) 100N C) 0.05N (D) 10N
Q.7 The S.I. unit of pressure is:
(A) atmosphere (B) dyne/cm2 C) pascal (D) mm of Hg
Q.9 The S.I. unit of thrust:
(A) N (B) dyne (C ) Nm2 (D) N m–2
Q.10 Pressure cannot be measured in:
(A) Nm2 (B) bar ( C) Pa (D) kg.wt.
Q.11 The total force exerted by the body perpendicular to the surface is called:
(A) pressure (B) thrust (C) impulse (D) none of these
Q.12 Pressure is a:
(A) scalar quantity
(B) normal force
(C) vector quantity
(D) all the above are wrong
Q.13 1 N/m2 equals:
(A) 1 Pa (B) 0.1 Pa (C) 0.01 Pa (D) 10 Pa
Q.14 The atmosphere exerts a pressure of P on the surface of earth, then P equals:
(A) 1.01 × 105 Nm–2 (B) 1.01 × 10–5 Nm–2
(C) 1.01 × 107 Nm–2 (D) 1.01 × 10–7 Nm–2
Q.15 Pressure exerted by a liquid column:
(A) Is independent of its density
(B) Is independent of the acceleration due to gravity
(C) Decreases with depth
(D) Is normal to the surface to vessel
Q.16 Thrust is a:
(A) Scalar quantity (B) Vector quantity
(C) Tangential force (D) None of these
Q.17 A piece of wood is held under water. The upthrust on it is:
(A) equal to the weight of the wood (B) less than the weight of the wood
(C) more than the weight of wood (D) zero
Q.18 Archimedes principle states that when a body is totally or partially immersed in a fluid the upthrust is equal to:
(A) the weight of the fluid displaced (B) the weight of the body
(C) volume of the fluid displaced (D) volume of the body
Q.19 S.I. unit of density is:
(A) kgm–2 (B) kgm–3 (C) m2kg–1 (D) N kg–1
Q.20 Unit of relative density is:
(A) kgm–3 (B) gcm–3 (C) m2litre–3 (D) it does not have a unit
Q.21 Relative density of a solid is 0.6. It floats in water with:
(A) whole of its volume inside water
(B) 60% volume inside water
(C) 60% volume outside water
(D) 40% volume inside water
Q.22 Buoyant force acting on a body due to different fluids is:
(A) same (B) different (C) zero (D) none of these
Q.23 The relative density of silver is 10.5, if the density of water is 1000 kgm–3, then density of silver will be:
(A) 10.5 kgm–3 (B) 1050 kgm–3 (C) 105 kgm–3 (D) 10500 kgm–3
Q.24 A boat full of iron nail is floating on water in a lake. When the iron nails are removed, the water level:
(A) rises (B) remains same (C) falls (D) nothing can be said
Q.26 A cylinder of wood floats vertically in water with one-fourth of its length out of water. The density of wood is:
(A) 0.25 g/cm3 (B) 0.5 g/cm3 (C) 0.75 g/cm3 (D) 1 g/cm3
Q.27 Relative density of a solid is:
(A) R.D. = (B) R.D. = (C) R.D. = (D) All of the above
Q.28 Archimedes principle is used to:
(A) design ships
(B) design Submarines
(C) design Lactometers
(D) all of them
Q.29 Two solids X and Y float on water, X floats with half of its volume submerged while Y floats with one-third of its volume out of water. The densities of X and Y are in the ratio of:
(A) 4 : 3 (B) 3 : 4 (C) 2 : 3 (D) 1 : 3
Q.30 The balloon stops rising up beyond a particular height when the density of gas inside the balloon:
(A) exceeds the density of air outside (B) equals the density of air
(C) becomes less than the density of air (D) none of the above
Q.31 A small iron ball suspended with spring balance weights 20 gm in air. Now it is completely dipped in water along with spring balance. Which of the following statement is/are correct:
(1) Both iron ball and spring balance will experience an upward force
(2) Only ball will experience upward force
(3) Spring balance will show more reading than before
(4) Spring balance will show less reading than before
(A) 1 & 4 are correct
(B) 2 & 3 are correct
(C) 1 & 3 are correct
(D) 2 & 4 are correct
Q.32 Two pieces of metal when completely immersed in a liquid have equal upthrust on them, then:
(A) Both pieces must have equal weights (B) Both pieces must have equal densities
(C) Both pieces must have equal volumes (D) Both are floating to the some depth
Q.33 Buoyant force is inversely proportional to:
(A) Volume body immersed in a liquid (B) Density of fluid
(C) Acceleration due to gravity
(D) Temperature of fluid
Q.34 As we move upwards, the atmosphere pressure:
(A) Increases (B) Decreases
(C) Remains same (D) Cannot be said
Q.35 If the mass of a body is 12.1 g and the density is 2.2 g/cc, its volume is: [NTSE]
(A) 5.5 cm3 (B) 8 cc (C) 11 cc (D) 55 cc
Q.36 Aluminium has a density of 2.7 g/cc. The mass of 15 cc of aluminium is: [NTSE]
(A) 45 g (B) 40.5 g (C) 80 g (D) 100 g
Q.37 Brine has a density of 1.2 g/cc. 40 cc of it are mixed with 30 cc of water. The density of solution is: [NTSE]
(A) 2.11 g/cc (B) 1.11 g/cc (C) 12.2 g/cc (D) 20.4 g/cc
Q.38 60 cc of a liquid of relative density 1.4 are mixed with 40 cc of another liquid of relative density 0.8. the density of the mixture is:
(A) 11.16 g/cc (B) 2.26 g/cc [NTSE]
(C) 11.6 g/cc (D) 116 g/cc
Q.39 If a force of 10N acts on surfaces of areas in the ratio 1 : 2, the thrust has the ratio:[NTSE]
(A) 1 : 2 (B) 2 : 1 (C) 3 : 1 (D) 1 : 1
Q.40 The height of mercury which exerts the same pressure as 20 cm of water column, is equal to
(A) 1.48 cm (B) 14.8 cm [NTSE]
(C) 148 cm (D) none of these
Q.41 The buoyant force depends on: [NTSE]
(A) depth of a liquid (B) colour of a liquid
(C) density of liquid (D) none of these
Q.42 The hot air balloon rises because it is:[NTSE]
(A) denser
(B) less denser
(C) equally dense
(D) the given statement is wrong
Q.43 A force of 50N is applied on a nail of area 0.001 sq. cm. Then the thrust is: [NTSE]
(A) 50N (B) 100N (C) 0.05N (D) 10N
Q.45 A piece of wood floats in water. What happens in alcohol? [NTSE]
(A) floats higher (B) stays as before (C) sinks (D) sinks and rises
Q.46 A boat full of iron nails are removed, the water level: [NTSE]
(A) rises
(B) falls
(C) remains the same
(D) nothing can be said
Q.47 An ice cube is floating in a glass of water. What happens to the water level when the ice melts? [NTSE]
(A) rises
(B) falls
(C) remains same
(D) first rises and then falls
Q.48 A solid weighs 32 gf in air and 28.8 in water. The R.D. of the solid is: [NTSE]
(A) 8.9 (B) 10 (C) 29.12 (D) 20
Q.49 A body of mass 50kg has a volume 0.049 m3. The buoyant force on it is: [NTSE]
(A) 50 kgf (B) 50 N (C) 49 N (D) 49 kgf
Q.50 If the density of a metal in 8.2 g/cc, its relative density is: [NTSE]
(A) 8.2 (B) 1/82 (C) 0/82 (D) none of these
Q.51 The SI unit of pressure is: [NTSE]
(A) atmosphere (B) dyne/cm2 (C) pascal (D) mm of Hg
Q.52 If two masses A and B have their masses in the ratio 1 : 4 and their volumes are equal, then their densities have the ratio: [NTSE]
(A) 1 : 4 (B) 4 : 1 ( C) 2 : 1 (D) 3 : 1
Q.54 If the density of a block is 981 kg/m3, it shall: [NTSE]
(A) sink (B) float
(C) float completely immersed in water (D) float completely out of water
Q.55 The R.D. of a metal block is 2.7 × 103 kg/m3. It is immersed in water. Then the metal block
(A) sinks [NTSE]
(B) floats
(C) is partially immersed
(D) has no part immersed
1. A 2. A 3. D 4. A
5. B 6. A 7. C 8. B
9. A 10. D 11. B 12. A
13. A 14. A 15. D 16. B
17. C 18. A 19. B 20. D
21. B 22. B 23. D 24. C
25. B 26. C 27. D 28. D
29. B 30. B 31. A 32. C
33. D 34. B 35. A 36. B
37. B 38. A 39. D 40. A
41. C 42. B 43. A 44. B
45. C 46. B 47. C 48. B
49. D 50. A 51. C 52. A
53. B 54. B 55. A