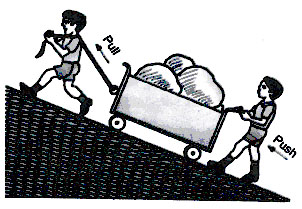
From our day to day experience, we all are familiar with the concept of 'Force'. While opening a door, lifting a bucket or a bag, kicking a football or throwing a stone, we have to act differently and in many ways. We are either pushing or pulling the object. No non-living object moves on its own. We have to apply the effort in the form of push or pull. This pull or push is called force. Thus a force is an external agency that displaces or tends to displace a body from its position of rest. The direction in which the object is pushed or pulled is called the direction of the force. Force has both magnitude and direction. It is a vector quantity.
Force is the 'push' or 'pull' which can make a body move, stop a moving body, change the direction and speed of a moving body. Force cannot be seen but the effect of force on an object can be seen or felt.
A force is physical quantity which causes or tends to cause a motion in an object at rest or changes or tends to change the direction of motion of a moving object or changes or tends to change the size and shape of an object or change or tends to change the speed of an object.
A force produces the following effects :-
Broadly speaking forces are classified as being of two types. (i) Contact force, (ii) Non-contact force
1. Contact force : The force which act on a body either directly or through some connector are called contact forces.
Examples : Biological force, muscular force, mechanical force and frictional force are the examples of contact force.
(a) Muscular Force : This force produced by the muscles of living beings is called muscular force or biological force.
(b) Mechanical Force : The force generated by machines are called mechanical force.
(c) Friction Force: A force which acts at the surface of contact, when one body moves or tends to move upon another body is called the force of friction.
(d) Resultant force : If a single force acting on a body produces
the same acceleration as produced by a number of forces, that single force is called the resultant of these individual forces.
(e) Normal Force :-
The force acting perpendicular to the ground surface then the
force is called normal force.
The force of friction has the following properties :
(i) It is produced only when one body is made to move upon another body.
(ii) It always opposes the motion of the body and tries to stop the body.
(iii) It wears off the surface of contact of two bodies.
It is the force of friction which makes it difficult for us to move heavy objects such as large boxes; carts laden with different kinds of substances, etc. Again, it is the force of friction which wears off the tyres of our bicycles, cars, trucks, etc.
2. Non-contact Force or Field force :
The force which do not make a direct contact with a body and act through space, without any connector are called non-contact force.
Examples:
(i) The force of gravity of the earth is a non-contact force which attracts all bodies towards the earth.
(ii) The electrostatics force can pull tiny bits of dry paper is a non-contact force.
(iii) A magnet can attract common pins of steel from a distance and hence the magnetic force is non-contact force.
(a) Gravitational Force :-
F=Gm1m2/r2 , Here G is a universal gravitational constant & m1 m2 are masses, and r is a distance between two bodies.
(b) Electrostatics Force :-
F=Kq1q2/r2 , Here K is a Coulomb's constant & q1 q2 are charges, and r is a distance between two charges.
(c) Magnetic Force: The strange property of some substances to attract iron or steel objects towards itself is called magnetic property. The substance which has the above property is called a magnet. As the objects of iron or steel move towards magnet, therefore we can say that they are acted upon by the force of magnet.
3. Balanced and unbalanced forces :
If a set of forces acting on a body produces no acceleration in it, the forces are said to be balanced. If it produces a non-zero acceleration, the forces are said to be unbalanced.
Definition of balance force :-
When two forces of equal magnitude but acting in opposite directions on an object simultaneously then the object continues in its state of rest of uniform motion in a straight line. Such forces acting on the object are known as balance force.
Examples of balanced force :-
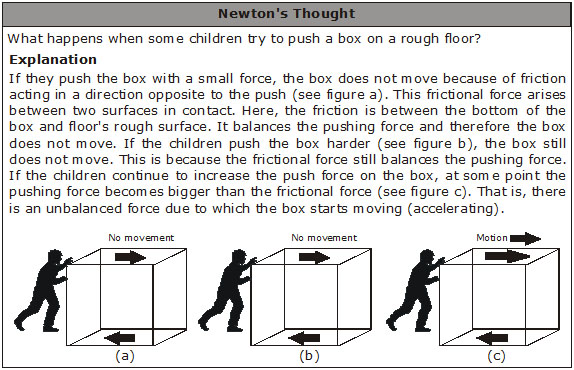
1. When we push a wall, the wall does not move at all i.e., it remains at rest.
In this case, the force of push on the wall acts in the forward direction. On the other hand, the wall also exerts equal force on our hand in the backward direction. These two equal and opposite forces cancel out the effect of each other and hence these two forces are the balanced forces.
2. When we try to push a heavy box on a rough surface, it does not move.
Definition of Unbalance force :-
When two forces of unequal magnitudes act in opposite directions on an object simultaneously then the object move in the direction of a large force. These forces acting on the object are known as unbalanced forces.
Examples of unbalanced force :-
1. When a boy drags a box on the floor, then an unbalanced force is acting on the box.
2. A bicycle will slow down if the rider stop pedaling it.
I.Newton's first law of motion :
A body at rest will remain at rest and a body in motion will remain in uniform motion unless an
unbalanced forces acts on it to change its state of rest or of uniform motion.
The above law can be understood in two parts.
(i) A body at rest remains at rest unless an external unbalanced force acts on it to change its state of rest.
Ex. Consider a wooden block kept on a horizontal surface at rest. It
will remain at rest unless somebody moves it.
(ii) A body in motion will remain in uniform motion unless an external unbalanced force acts on it to change its state of uniform motion.
(i) There is an inherent property of an object by virtue of which it cannot change its state of motion or rest by itself. This property is called 'inertia'.
(ii) Inertia is of two types– inertia of rest and inertia of motion.
(A) Inertia of rest:
If the body is at rest, it will continue to be at rest unless some external force is applied on it. Examples are following.
(i) When a train at rest starts moving suddenly, a passenger standing inside the compartment tends to fall backward.
(ii) When a carpet is beaten up with a stick, the dust particles are detached.
(iii) When a bullet is fired into a glass pane, it pierces a hole only at the point where the bullet hits the glass without breaking the entire glass pane into pieces.
(B) Inertia of motion :
When a body is in uniform motion, it will continue to remain in its uniform motion, i.e. it resists any change in its state of motion due to inertia of motion.
(i) when a person jumps out of a moving bus, he should run in the direction in which bus is moving otherwise he will fall down.
(ii) A train moving with a uniform speed and if a ball is thrown upwards inside the train by a passenger, then the ball comes back to his hand.
Mass and Inertia :
(i) Larger the mass of the body, larger is the inertia.
(ii) eg. it is more difficult to stop a cricket ball than a tennis ball.

(i) Gravitational mass of a body is the inherent property measured by a physical balance or beam balance.
(ii) When the balance beam becomes horizontal then the masses on both the pans are equal because the force of gravity experienced by both the masses is equal.
(iii) Gravitational mass of a body does not depend on the place where it is measured, i.e. it will be the same on the earth as well as on the moon.
(iv) Inertial mass is related to the motion of the body while the gravitational mass is related to the force of attraction in equilibrium.
(v) Both of them are proportional to the quantity of matter contained in the body.
(vi) Both of them have additive property.
(vii) None of them is affected by chemical changes.
(viii) Both of them have same units, i.e. kilogram.
Definition :
The product of mass and velocity of a body is called Linear momentum, it is denoted by P.
Linear momentum = mass × velocity
² Conclusion :-
(a) The momentum of the moving body is proportional to
(i) mass of the body and (ii) velocity of the body.
(b) Momentum is a vector quantity.
(c) Magnitude of momentum, P = mass × speed
P = mv
(d) Direction of momentum of a body is same as that of the direction of the velocity of the body.
Momentum = mass × velocity
\ Unit of momentum = unit of mass × unit of velocity
(i) S.I. unit of momentum is kg ms–1.
(ii) In CGS system, unit of momentum is g cm–1.
(iii) The other unit of momentum is N-s.
Note:
(i) Linear momentum has a sense of direction. Therefore it is a vector quantity.
(ii) The direction of linear momentum of a body at any instant is same as that of the velocity of the body at that instant.
(iii) A body moving in a curved path, the direction of velocity at a point is a tangent drawn at that point. Therefore, the direction of linear momentum is also tangential.
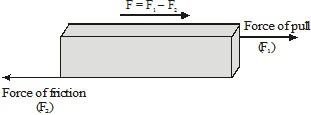
According to this law, the change in momentum of a body per unit time (i.e. rate of change of momentum) is directly proportional to the unbalanced force acting on the body and the change in momentum takes place in the direction of the unbalanced force on the body.
where, dp = change in momentum and dt = time taken for this change in momentum.
Consider a body of mass m moving with initial velocity u. Let a force F acts on the body for time t .
Initial momentum of the body, Pi = mu
Final momentum of the body, Pf = mv
Now, change in momentum of the body = Pf – Pi = mu – mu = m(v – u)

Then from equation (ii) 1 = k or k = 1
Put this value of k = 1 in equation (ii), we get
Thus, force acting on the body is directly proportional to (i) its mass (m) and (ii) its acceleration (a).
Equation (i) gives the mathematical form of Newton's second law of motion.
We know, F = ma
If m = 1 unit and a = 1 unit
Then F = 1 unit
SI unit of force :-
We know, F = ma
SI unit of mass,m = 1 kg
SI unit of acceleration, a = 1 ms–2
SI unit of force = 1 kg × 1 ms–2 = 1 kg ms–2.
1 kg ms–2 is known as 1 newton (N).
1 newton (N) = 1 kg ms–2
(i) Definition of Newton (N) :-
The force is said to be 1 newton if it products 1 ms–2 acceleration in a body of 1 kg mass.
C.G.S. unit of force :-
We know, F = ma
In CGS system, unit of mass, m = 1 g
unit of acceleration, a = 1 cm s–2
unit of force = 1 g × 1 cm s–2 = 1 g cm s–2
1 g cm s–2 is known as 1 dyne
1 dyne = 1 g cm s–2
(ii) Definition of Dyne :-
The force is said to be 1 dyne if it produces 1 cm s–2 acceleration in a body of 1 g mass.
We know, 1 newton (N) = 1 kg ms–2 ... (i)
Now 1 kg = 1000 g = 103 g
1 m = 100 cm = 102 cm
Put these values in equation (i), we get
\ 1 newton = 103 g × 102 cm s–2 = 105 g cm s–2
But 1 g cm s–2 = 1 dyne
\ 1 newton = 105 dyne
² Newton's Second Law in Terms of Linear Momentum
Definition : The rate of change of momentum of a body with respect to time is directly proportional to the external force acting on the body and takes place in the direction of force.
Suppose a body of mass m is acted upon by an unbalanced external force F which creates an acceleration a in the body. Let the initial velocity of the body be u. Let the force continues to act for a time interval t and the final velocity of the body be v. Then we can write

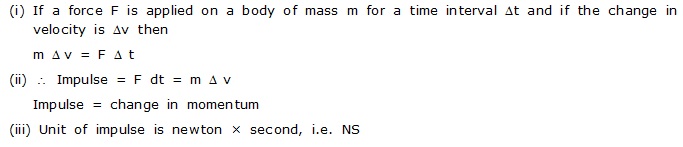
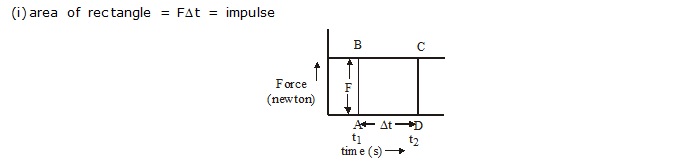
(i) A bullet fired from a gun with a large velocity resulting in a large momentum when strikes a body, its velocity becomes zero in a short interval of time.
(ii) The rate of change of momentum is very large and it exerts a large force and so that it can easily pierce the body.
(iii) While catching a cricket ball a player moves his hands backwards. Cricket ball coming towards fielder has a large momentum. By doing so he increases the time interval to reduce the momentum of the ball. Rate of change of momentum becomes slow.
(iv) The ball exerts lesser force.
(v) He does not get hurt.
Definition : For each and every action, there is equal and opposite reaction.
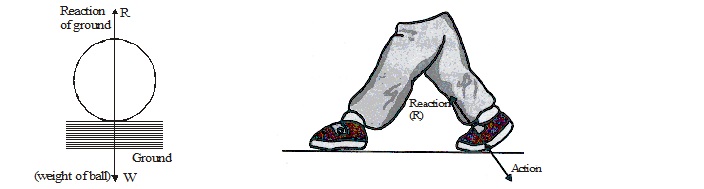
lf a body A exerts force on another body B, then B exerts a force – on A, the two forces acting along the same line. The two forces and – connected by Newton's third law are called action-reaction pair. Any one may be called 'action' and the other 'reaction'.
Action and reaction acts on different bodies hence they never cancel each other.
Note : Action and reactions forces occur simultaneously. It is wrong to think that first action occurs and it is followed by reaction.
An important conclusion :- When action-reaction forces are acting on two bodies of masses mA and mB then

Misconception : The action and reaction forces acting on a body are equal and opposite
and therefore cancel out the effect of each other.
Concept : Action and reaction do not cancel out the effect of each other because they act on different bodies.
Misconception : Any pair of equal and opposite forces is a action-reaction pair.
Concept : Only those forces from an action-reaction pair which involve the two bodies
responsible for action-reaction.
1. When a bullet is fired from a gun, we observe recoiling of the gun. The gun acts on bullet i.e., exerts a force on the bullet; simultaneously, the bullet reacts on the gun.
2. While walking or running, you push the ground in the backward direction with your feet. The ground simultaneously exerts a force of equal magnified in the forward direction on feet. This force enables us to walk.
3. When a man jumps from a boat, the boat also experiences a backward jerk. This is due to the action-reaction pair as shown in figure.
4. Inflate a balloon and leave it. You will observe that the balloon moves in opposite direction to the opening in balloon through which the air is coming out.
5. A ball rebounds after striking against a floor.
When a ball strikes against a floor, it exerts a force on the floor. According to Newton's third law of motion, the floor exerts an equal and opposite force on the ball. Due to this reaction, the ball rebounds.
6.How do we swim ?
While swimming, a swimmer pushes the water backward with his hands. The reaction offered by the water to the swimmer pushes him forward.
7. A boatman pushes the river bank with a bamboo pole to take his boat into the river.
When the boatman pushes the river bank with a bamboo pole, the river bank offers an equal and opposite reaction. This reaction helps the boat to move into the river.
8. Why a fireman struggles to hold a hose-pipe ?
A fireman has to make a great effort to hold a hose-pipe to throw a stream of water on fire to extinguish it. This is because the stream of water rushing through the hose-pipe in the forward direction with a large speed exerts a large force on the hose-pipe in the backward direction.
We know that if a moving body strikes a body at rest, the moving body slows down and the stationary body starts moving. Whereas the first body loses momentum, the second body gains momentum. We shall observe that the total momentum before impact is equal to total momentum after impact.
If two bodies of masses m1, m2 are initially moving with velocities u1, u2 and after collision they start moving with velocities vI and v2 respectively, then
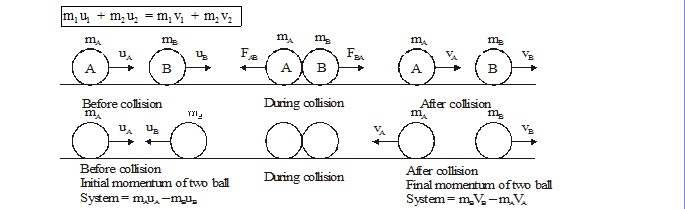
i.e., total momentum before collision is equal to total momentum after impact.
If one body gains momentum, the other loses an equal amount of momentum.
Proof of the law of conservation of linear momentum:
Consider a system consisting of two bodies A and B of (say glass spheres) masses m1 and m2 respectively. Let these bodies are moving with velocities u1 and u2 as shown in figure. Let u1 > u2. Let these bodies collide with each other for a small interval of time 'dt'. At the time of collision, body A exerts a force F on body B and body B exerts equal and opposite force (– F) on body A. Due to these forces, the momentum of the bodies changes. Let n1 and n2 be the velocities of body A and body B respectively after the collision.
Initial momentum of body A = m1 u1
Initial momentum of body B = m2 u2
Final momentum of body A = m1 v1
Final momentum of body B = m2 v2
Total momentum of the system before collision = m1u1 + m2u2
Total momentum of the system after collision = m1v1 + m2v2
Now, the rate of change of momentum of body A

i.e. Total momentum of the system (i.e. bodies A and B) before collision
= Total momentum of the system (i.e. bodies A and B) after collision.
This is the law of conservation of linear momentum.
Examples to illustrate the law of conservation of momentum
1. Recoil of a gun. The recoil of a gun can be explained with the help of the law of conservation of momentum.
The bullet inside the gun and the gun itself form a system. Thus, the system is gun + bullet. Before firing, the gun and the bullet are at rest, therefore, momentum of the system before firing is zero.
When the bullet is fired, it leaves the gun in the forward direction with certain momentum. Since no external force acts on the system, so the momentum of the system (gun + bullet) must be zero after firing. This is possible only if the gun moves backward with a momentum equal to the momentum of the bullet. That is, why gun recoils or moves backward figure.
Recoil Velocity. The velocity with which the gun moves backward after firing a bullet is known as recoil velocity.

Negative sign shows that the direction of the velocity of the gun after firing is opposite to the direction of the velocity of the bullet.
The movement of a rocket in the upward direction can also be explained with the help of the law of conservation of momentum.
The momentum of a rocket before it is fired is zero. When the rocket is fired, gases are produced in the combustion chamber of the rocket due to the burning of fuel. These gases come out of the rear of the rocket with high speed. The direction of the momentum of the gases coming out of the rocket is in the downward direction. To conserve the momentum of the system (rocket + gases), the rocket moves upward with a momentum equal to the momentum of the gases. The rocket continues to move upward as long as the gases are ejected out of the rocket.
3. Inflated balloon lying on the surface of a floor moves forward when pierced with a pin.
The momentum of the inflated balloon before it is pierced with a pin is zero. When it is pierced with a pin. air in it comes out with a speed in the backward direction. To conserve the momentum, the balloon moves in the forward direction.
Friction
If the switch off the engine of car it will stop after moving a certain distance. It means that some retarding force is acting on the car which stops it. The force opposing the motion of the car is called "force of friction".
(i) The frictional force is tangential to the surface in contact and always in a direction opposite to the direction of motion of the object.
(ii) Frictional force is a force opposing the relative motion between two surfaces which are in contact with each other.
(iii) The force of friction arises due to the interlocking of irregular projections on the two surfaces and is called as "force of contact".
(A) Static friction :
The frictional force that exists between the body and the surface so long as they are relatively at rest even when the external force acts, is called the static friction.
(B) Limiting friction :
(i) When there is no external force acting on the body, the frictional force is zero.
(ii) If we increase the magnitude of the external force, the static friction also increases.
(iii) At one pt, when there is a slight increase in the magnitude of the external force, the body just starts sliding over the surface.
(iv) The force of friction at the limiting stage is called the 'limiting friction.'
(v) The limiting friction depends upon the nature of the two surfaces in contact.
(C) Kinetic or Sliding friction :
(i) When the external force exceeds the limiting friction, the body just starts sliding.
(ii) The minimum force required to maintain the motion of the body over the other surface is called the "kinetic friction".
(iii) The frictional force that exists between the two surfaces when there is a uniform relative motion between them is called the "dynamic friction" or "sliding friction".
(iv) Kinetic friction is smaller than the limiting friction.
(D) Rolling friction :
(i) The frictional force that exists between the two surfaces when a body rolls over the other is called the "rolling friction".
(ii) It deforms the surface over which it rolls.
(iii) Rolling body it-self gets deformed at the pt of contact over the surface.
(i) The part OA of the graph shows that the static friction increases with the increase in applied force.
(ii) The force of friction is maximum at a pt A which is equal to AP.
(iii) If the applied force is increased further, the body will continue to be in motion but the force of friction is slightly lesser.
(iv) After this the force of friction remains constant.
Note : Rolling friction is smaller than sliding friction which in turn is smaller than the limiting friction.
The force of friction depends upon the following factors :
(i) Materials of the bodies in contact.
(ii) Roughness of the surfaces in contact
(iii) Force of friction is independent of the area of the two surfaces in contact.
(iv) The limiting frictional force is directly proportional to the normal reaction.
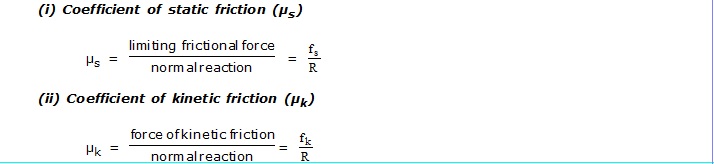
Frictional force can be reduced in the following ways:
1. Use of lubricants : In machines, friction can be reduced by applying lubricants between the contact surfaces to fill the fine pores or depressions in the surfaces and make them smooth thereby reducing friction.
2. Polishing : unevenness of the surfaces can be reduced by polishing, thereby reducing the friction.
3. Use of ball bearings : In rotating machines, shafts are mounted on ball bearings. By doing so, rolling friction occurs lesser than sliding friction, thereby reducing the friction.
4. By streamlining : Air friction is reduced by designing streamlined bodies of cars or aeroplanes. Similarly, if the bodies of boats and ships are streamlined, friction of water can be reduced.
5. Wheels: If a suitcase is fitted with wheels,it is easier to move it because the friction between the wheels and the ground is less.
1. Wear and Tear : In machine parts like gears, brakes when they come in contact with each
other continuously, they wear out gradually, which should be replaced time to time.
2. Friction reduces efficiency of the machine.
3. Friction in machine produces heat and undesirable noise which damages the machine. To avoid excessive heating, water is circulated in machines generally.
1. We would not be able to walk if there had been no friction b/w the soles of our shoes and the ground.
2. If there had been no friction, the wheels of a car will slip instead of rotating and stop moving. For that we have to increase the friction by making the tyres corrugated to get better grip of tyres on the road. Also, the friction is increased.
3. When brakes are applied, the vehicle stops due to the force of friction b/w the brake lining and the drum.
4. In the absence of friction, we cannot write on a blackboard with a chalk stick because the chalk stick will slide off the board without leaving any mark on the board.
Ex.1 Which of the following has more inertia :
(a) a rubber ball and a stone of the same size ?
(b) a bicycle and a train ?
(c) a five rupees coin and one-rupee coin ?
Sol. Mass of a body is the measure of its inertia; i.e., more the mass more is the inertia. Keeping this in mind :
(a) Stone has more inertia.
(b) Train has more inertia.
(c) Five rupees coin has more inertia.
Ex.2 In the following example, try to identify the number of times the velocity of the ball changes.
“A football player kicks a football to another player of his team who kicks the football towards the goal. The goalkeeper of the opposite team collects the football and kicks it towards a player of his own team : Also identify the agent supplying the force in each case.
Sol. The velocity of the football changes four times
First time the velocity changes when the player applies force to kick the ball towards another player of his team.
Second time the velocity changes when the other player kicks the ball towards the goal.
Third time the velocity changes when the goalkeeper collects the ball by applying force in the direction opposite to the direction of the motion of the ball.
Fourth time the velocity changes when the goalkeeper kicks the ball towards the player of his own team by applying force.
Ex.3 Explain why some of the leaves may get detached from a tree if we vigorously shake its branch.
Sol. When the branch is suddenly set in motion, the leaves attached to it tend to continue in their state of rest because of inertia of rest. It generates a lot of strain at the junction of leaves and the branch. Because of this strain some leaves get detached from the branch.
Ex.4 Why do you fall in the forward direction when a moving bus apply brakes to stop and fall backward when it accelerates from rest ?
Sol. The bus and the persons in it are in the state of motion before the application of the brakes. When the brakes are suddenly applied, the bus comes to the state of rest, the lower part of passengers which is in contact with bus comes to rest, but the upper part tends to continue in the state of motion because of inertia of motion. Therefore, they fall in forward direction. Conversely, when the bus is in the state of rest, the passengers in it have inertia of rest. When the bus accelerates suddenly, the passengers tend to continue in their state of rest and hence are left behind, relative to the position of bus. Therefore, they fall in the backward direction.
Ex.5 If action is always equal to the reaction, explain how a horse can pull a cart.
Sol. When a horse pulls a cart with a certain force, then the cart pulls the horse with the same force and the system of horse and cart should not move.
But, if we analyze the problem carefully, then horse not only applies force on the cart, but also pushes the earth backward with his feet. The earth reacts back in this action of the horse and pushes it in the forward direction. The force applied by the horse on the earth is insufficient to move the earth, but the force applied by the earth is sufficient to make the horse to move in the forward direction.
This unbalanced force applied by the earth makes the system of horse and cart to move in the forward direction.
Ex.6 Explain, why is it difficult for a fireman to hold a hose pipe, which ejects large amounts of water at high velocity.
Sol. We can explain the above observation on the basis of law of conservation of momentum. When a system of the hose and water is not ejecting any water its momentum is zero. When the water issues out from the hose with a high velocity, it has momentum in the forward direction. Therefore, in order to conserve momentum the hose tends to move in the backward direction and hence is difficult to hold.
Ex.7 From a rifle of mass 4 kg, a bullet of mass 50 g is fired with an initial velocity of
35 ms–1. Calculate the initial recoil velocity of the rifle.
Sol. Initial mass of rifle = 4 kg
Let initial velocity of recoil of rifle = v
Initial momentum of the rifle = 4 x v
Initial mass of bullet = 50 g
=
Initial velocity of bullet = 35 ms–1
Initial momentum of bullet = 0.05 × 35
Using the law of conservation of momentum ;
Momentum of the rifle = Momentum of the bullet
4 × v = 0.05 × 35
v = 0.05*35/4
v = 0.4375 ms–1
Ex.8 Two objects of masses 100 g and 200 g are moving along the same line and direction, with velocities 2 ms–1 and 1 ms–1, respectively.
They collide and after the, collision, the second object moves with a velocity of 1.67 ms–1. Determine the velocity of the first object.
Sol.
Let the 100 g and 200 g objects be A and B as shown in above figure.
Initial momentum of A = 100 × 2 = 200 g ms–1
Initial momentum of B = 200 × 1 = 200 g ms–1
\ Total momentum of A and B before collision
= 200 + 200 = 400 g ms–1
Let the velocity of A after collision = V
\ Momentum of A after collision = 100 × V
Also, Momentum of B after collision
= 200 × 1.67 = 334 g ms–1
\ Total momentum of A and B after collision
= 100 × V + 334
Using the Law of conservation of momentum.
Momentum of A and B after collision = Momentum of A and B before collision
100 × V + 334 = 400
100 × V = 400 – 334
Þ V =
V = 0.66 ms–1
Ex.9 An object experiences a net zero external unbalanced force. Is it possible for the object to be travelling with a non-zero velocity ? If yes, state the conditions that must be placed on the magnitude and direction of the velocity. If no, provide a reason.
Sol. No, the object will not be able to travel with non-zero velocity because there is net zero external unbalanced force. However, this will apply only on the surface of the earth where forces of gravity and friction always act on the object.
If the object is in deep space and is completely free from the forces of friction and gravitation, such that it is moving with non-zero velocity, then it will continue moving with the same velocity and in the same direction.
Ex.10 When a carpet is beaten with a stick, dust comes out of it. Explain.
Sol. Initially, the carpet and loose dust in it are in the state of rest. When the carpet is hit with a stick, it is suddenly set into motion, but the loose dust in it remains in the state of rest because of inertia of rest. Thus, in a way dust is left behind relative to carpet and hence comes out in air.
Ex.11 Why it is advised to tie any luggage kept on the roof of a bus with a rope?
Sol. Luggage on the top of the bus is a loose fixture and not a compact part of the bus. Thus, when a speeding bus brakes suddenly, the luggage continues moving forward because of inertia of motion and is likely to fall off the bus. Conversely, if a stationary bus accelerates suddenly, the luggage continues in the same state because of inertia of rest and hence is left behind relative to bus such that it falls backward. To avoid the falling of luggage, it is tied with a rope.
Ex.12 A batsman hits a cricket ball which then rolls on a level ground. After covering a short distance, the ball comes to rest. The ball slows to a stop because,
(a) the batsman did not hit the ball hard enough.
(b) velocity is proportional to the force exerted on the ball.
(c) there is a force on the ball opposing the motion.
(d) there is no unbalanced force on the ball, so the ball would want to come to rest.
Sol. Correct Answer : (c)
There is force on the ball opposing the motion.
This force is the force of friction between the ball and the surface of ground.
Ex.13 A truck starts from rest and rolls down a hill with a constant acceleration. It travels a distance of 400 m in 20 s. Find its acceleration. Find the force acting on it if its mass is 7 metric tonnes
(Hint : 1 metric tonne = 1000 kg.)
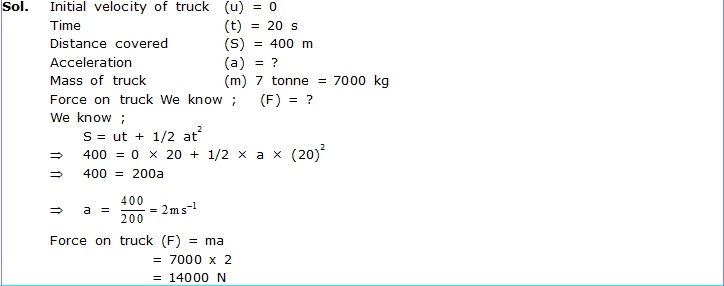
Ex.14 A stone of 1 kg is thrown with a velocity of 20 ms–1 across the frozen surface of a lake and comes to rest after travelling a distance of 50 m. What is the force of friction between the stone and the ice ?
Sol. Mass of stone (m) = 1 kg
Initial velocity of stone (u) = 20 ms–1
Final velocity of stone (v) = 0
Distance covered by the stone (s) = 50 m
Acceleration of stone (a) = ?
Force acting on the stone due to friction (F) = ?
We know : v2 – u2 = 2as
(0)2 – (20)2 = 2a × 50
– 400 = 100 a
a = = – 4
a = – 4 ms–2
\ Force of friction (F) = ma
= 1 × (– 4)
= – 4N
Negative sign signifies that force of friction is acting in the direction opposite to the direction of motion of the stone.
Ex.15 A 8000 kg engine pulls a train of 5 wagons, each of 2000 kg, along a horizontal track. If the engine exerts a force of 40000 N and the track offers a frictional force of 5000 N, then calculate:
(a) the net accelerating force;
(b) the acceleration of the train, and
(c) the force of wagon 1 on wagon 2.
Sol. (a) Force exerted by the engine = 40,000 N
Force of friction exerted by the tracks = 5000 N
As the force of friction always acts opposite to the direction of applied force.
\ Net accelerating force of engine
= 40000 – 5000 = 35000 N
(b) Mass 5 wagons
= 2000 × 5 = 10000 kg
We know : F = ma
35000 = 10000 × a
Þ 35000/10000 = 3.5m/s2
(c) Force of wagon 1 on wagon 2
F = ma
= 8000 × 3.5 = 28000 N
Ex.16 An automobile vehicle has a mass of 1500 kg. What must be the force between the vehicle and road if the vehicle is to be stopped with a negative acceleration of 1.7 ms–2 ?
Sol. Mass of the vehicle (m) = 1500 kg
Negative acceleration (a) = –1.7 ms–2
\ Force of friction between the road and vehicle
F = ma
F = 1500 × (–1.7) = – 2550 N
Negative sign means force is acting in the direction opposite to the direction of motion of the vehicle.
Ex.17 What is the momentum of an object of mass m, moving with a velocity v ?
(a) (mv)2 (b) mv2 (c) 1/2mv2 (d) mv
Sol. Correct Answer : mv
Ex.18 Using a horizontal force of 200 N, we intend to move a wooden cabinet across a floor at a constant velocity. What is the friction force that will be exerted on the cabinet ?
Sol. In order to move the cabinet with constant velocity, the net force acting on it should be zero, such that the forces are balanced.
This is possible only, if the frictional force is 200 N and acts in the direction opposite to the direction of motion of the cabinet.
Ex.19 Two objects, each of mass 1.5 kg, are moving in the same straight line but in opposite directions. The velocity of each object is 2.5 ms-’ before the collision during which they stick together. What will be the velocity of the combined object after collision ?
Sol. Let the object be A and B moving from opposite direction in the same straight line.
\ Momentum of A = m × v
= 1.5 x2.5 = 3.75 kg ms–1
Also, Momentum of B
= m × (–v)
= 1.5 × (–2.5) = –3.75 kg ms–1.
If, v is the velocity of the objects after collision, then Combined momentum after collision
= 3 × v
Using the law of conservation of momentum
Combined momentum of A and B = Momentum of A + Momentum of B
3 × v = 3.75 – 3.75
Þ 3 × v = 0
Þ v = 0
Ex.20 According to the third law of motion when we push on an object, the object pushes back on us with an equal and opposite force. If the object is a massive truck parked along the roadside, it, will probably not move. A student justifies this by answering that the two opposite and equal force cancel each other Comment on this logic and explain why the truck does not move.
Sol. The logic of the boy is completely wrong because the truck is going to move only due to the unbalanced force which is produced when the boy pushes the earth with his feet in the backward direction. However, this force produced by the reaction of earth is insufficient to overcome the force of friction offered by the wheels of the truck and hence, it does not move.
Q.1 A hockey ball of mass 200g travelling at 10 ms–1 is struck by a hockey stick so as to return it along its original path with a velocity of 5 ms–1. Calculate the change of momentum which occurred in the motion of the hockey ball by the force applied by the hockey stick.
Ans. Mass of ball, m = 200g = 0.2kg: initial velocity of ball, u1 = 10 ms–1; final velocity of ball, u2 = –5 ms–1.
(Negative sign denotes that ball is moving in opposite direction)
Initial momentum of ball = mu1 = 0.2 × 10 = 2 Ns
Final momentum of ball = mu2 = 0.2 × (–5) = –1 Ns
\ Change in momentum =
Final momentum – initial momentum = (–1) – (2) = – 3 Ns
Negative sign denotes that change in momentum is in the direction opposite to the direction of initial momentum of the ball.
Q.2 A bullet of mass 10 g travelling horizontally with a velocity of 150 ms–1 strikes a stationary wooden block and comes to rest in 0.03s. Calculate the distance of penetration of the bullet into the block. Also calculate the magnitude of the force exerted by the wooden block on the bullet.
Ans. Mass of bullet, m = 10g = 0.01 kg; initial velocity of bullet, u = 150 ms–1; final velocity of bullet, v = 0; time, t = 0.03s; acceleration of bullet, a = ?; force exerted by wooden block, F = ?; distance penetrated by bullet, s = ?
We know, v = u + at
or 0 = 150 + a × 0.03
or –a × 0.03 = 150
or a = = –5000 ms–2
We know, s = ut + at2
= 150 × 0.03 + × (–5000) × (0.03)2
= 4.5 – 2.25 = 2.25 m
We know, F = ma
Force acting on bullet,
F = 0.01 × (–5000) = – 50 N
Negative sign denotes that wooden block exerts force in a direction opposite to the direction of motion of the bullet.
Q.3 An object of mass 1 kg travelling in a straight line with a velocity of 10 ms–1 collides with, and sticks to a stationary wooden block of mass 5 kg. Then they both move off together in the same straight line. Calculate the total momentum just before the impact and just after the impact. Also, calculate the velocity of the combined object.
Ans. For object: m1 = 1kg; u1 = 10 ms–1
For wooden block; m2 = 5 kg; u2 = 0
Momentum just before collision = m1u1 + m2u2 = 1 × 10 + 5 × 0 = 10 kg ms–1
Since, momentum is conserved, momentum before collision = momentum after collision = 10 kg ms–1
Mass after collision = (m1 + m2) = 1 + 5 = 6 kg
Let velocity after collision = v
\ Momentum after collision = 6 × v
Using the law of conservation of momentum, momentum after collision = momentum before collision
\ 6 × v = 10 or v = 10/6 = 1.67 ms–1
Q.4 An object of mass 100 kg is accelerated uniformly from a velocity of 5 ms–1 to 8 ms–1 in 6 s. Calculate the initial and final momentum of the object. Also, find the magnitude of the force exerted on the object.
Ans. Mass of object, m = 100 kg; initial velocity, u = 5 ms–1; final velocity, v = 8 ms–1; time, t = 6 s
Initial momentum = mu = 100 × 5 = 500 Ns
Final momentum mv = 100 × 8 = 800 Ns
Force exerted on the object
F = mv-mu/t = 800-500/6 = 300/6 = 50 N
Q.5 Akhtar, Kiran and Rahul were riding in a motorcar that was moving with a high velocity on an expressway when an insect hit the windshield and got stuck on the windscreen, Akhtar and Kiran started pondering over the situation. Kiran suggested that the insect suffered a greater change in
momentum as compared to the change in momentum of the motorcar (because the change in the velocity of the insect was much more than that of the motorcar). Akhtar said that since the motorcar was moving with a larger velocity, it exerted a larger force on the insect. And as a result the insect died. Rahul while putting an entirely new explanation said that both the motorcar and the insect experienced the same force and change in their momentum. Comment on these suggestions.
Ans. Kiran’s suggestion is not correct because momentum is always conserved i.e. change in momentum of insect must be equal and opposite to that of motorcar.
Akhtar’s suggestion is also not correct.
Rahul’s suggestion is correct i.e., insect and motorcar experience same force and change in momentum.
However, the insect dies, because it is unable to bear the large force and large change in momentum.
Q.6 How much momentum will a dumb-bell of mass 10 kg transfer to the floor if it falls from a height of 80 cm and does not rebound? Take its downward acceleration to be 10 ms–2.
Ans. Mass of dumb-bell, m = 10kg; initial velocity, u = 0; final velocity, v = ?; distance, s = 80 cm = 0.8 m; acceleration, a = 10 ms–2
We know v2 – u2 = 2as

\ Momentum of dumb-bell transferred to ground = mv = 10 × 4 = 40 kg ms–1.
Q.7 The following is the distance-time table of an object in motion
(a) What conclusion can you draw about the acceleration? Is it constant, increasing, decreasing or zero?
(b) What do you infer about the force acting on the object?

Q.8 Two persons manage to push a motorcar of mass 1200 kg at a uniform velocity along a level road. The same motorcar can be pushed by three persons to produce an acceleration of 0.2 ms–2. With what force does each person push the motorcar? (Assume that all persons push the motorcar with the same muscular effort.)
Ans. As two persons can make the motorcar move with uniform velocity, it is clear that total force applied by them on the motorcar is balanced by the force of friction acting in the opposite direction. It is force of one more person which produces an acceleration of 0.2 ms–2.
\ Force of one person mass × acceleration 1200 × 0.2 = 240 N
Q.9 A hammer of mass 500 g, moving at 50 ms–1, strikes a nail. The nail stops the hammer in a very short time of 0.01 s. What is the force of the nail on the hammer?
Ans. the force of nail on the hammer

Negative sign denotes that the force of nail on the hammer is acting in the direction opposite to that of motion of hammer.
Q.10 A motorcar of mass 1200 kg is moving along a straight line with a uniform velocity of 90 km/h. Its velocity is slowed down to 18 km/h in 4 s by an unbalanced external force. Calculate the acceleration and change in momentum. Also calculate the magnitude of the force required.

Q.11 A large truck and a car, both moving with a velocity of magnitude v, have a head-on collision. If the collision lasts for 1 s,
(a) Which vehicle experiences greater force of impact ?
(b) Which vehicle experiences greater change in momentum?
(c) Which vehicle experiences greater acceleration?
(d) Why is the car likely to suffer more damage than the truck?
Ans. Let mass of truck M; mass of car m; velocity of truck = v; time for which collision lasts, t = 1s; velocity of car = -v (Negative sign for opposite direction of motion).
(a) On collision, both the vehicles experience the same force, as action and reaction are equal.
(b) Change in momentum of truck is equal and opposite to change in momentum of car, i.e., both the vehicles experience the same change in momentum.
(c) As acceleration = force/mass, and force on each vehicle is same, therefore, acceleration As mass of car is smaller, therefore, acceleration of car is greater than the acceleration of the truck.
(d) The car is likely to suffer more damage than the truck, as it is lighter. The acceleration i.e. change in velocity/s of car is more than that of the truck.
Q.1 Give two examples in each case, of a force that:
(i) Lifts (ii) Pushes (iii) Pulls (iv) Stretches (v) Compresses
(vi) Resists (vii) Attract (viii) Squeeze.
Q.2 State and explain the law of inertia
(or Newton’s first law of motion)
Q.3 You are hurt when you kick a stone. Why?
Q.4 Give an example of a force that merely changes the direction of motion of a body.
Q.5 Define (i) force (ii) dyne (iii) newton.
Q.6 State Newton’s second law of motion.
Q.7 What is the SI unit of force ?
Q.8 Name the cgs unit of force. How is it related to Newton ?
Q.9. While standing in a bus, we fall backward if the bus suddenly starts. Why?
Q.10 The passengers fall forward when a speeding bus stops suddenly. Why?
Q.11 Newton’s first law of motion is also called law of inertia. Why?
Q.12 Air is thrown on a sail attached to a boat from an electric fan placed on the boat. Will the boat start moving?
Q.13 A bird is sitting on the floor of a wire cage and the cage is in the hand of a boy the bird starts flying in the cage. Is there any change in the weight of the cage?
Q.14 There is some water is the beaker placed on the pan of a spring balance. If we dip one finger in this water without touching the bottom of the beaker, then what would be the effect on the reading of the balance?
Q.15 An athlete always runs some distance before taking a jump? Why?
Q.16 According to Newton’s third law, every force is accompanied by equal and opposite forces how then can anything move?
Q.17 Give the magnitude and direction of the net force acting on.
(a) a drop of rain falling down with a constant speed.
(b) a cork of mass 10 g floating on water.
(c) a kite skilfully held stationary in the sky.
Q.18 Calculate the force required to produce an acceleration of 5 m/s2 in a body of mass 2.4 kg.
Q.19 A body of mass 2.5 kg is moving with a velocity of 20 m/s. Calculate its momentum.
Q.20 A force acts for 0.2 s on a body of mass 2.5 kg initially at rest. The force then ceases to act and the body moves through 4m in the next one second. Calculate the magnitude of force.
Q.21 A ball of mass 20 gm is initially moving with a velocity of 100 m/s. On applying a constant force on the ball for 0.5s, it acquires a velocity of 150 m/s. Calculate the following :
(i) Initial momentum of the ball
(ii) Final momentum of the ball
(iii) Rate of change of momentum
(iv) Acceleration of the ball
(v) Magnitude of the force applied
Q.22 A cricket ball of mass 200 gm moving with a speed of 40 m/s is brought to rest by a player in 0.04s. Calculate the following :
(i) Change in momentum of the ball,
(ii) Average force applied by the player.
Q.23 A motorcycle is moving with a velocity of 108 km/hr and it takes 5 s to stop it after the brakes are applied. Calculate the force exerted by the brakes on the motorcycle if its mass along with the rider is 250 kg.
Q.24 A rifle of mass 5 kg fires a bullet of mass 40 gm. The bullet leaves the barrel of the rifle with a velocity 200 m/s. If the bullet takes 0.004 s to move through the barrel, calculate the following:
(i) recoil velocity of the rifle and
(ii) the force experienced by the rifle due to its recoil.
Q.25 A bullet of mass 20 gm moving with a velocity 200 m/s gets embedded into a wooden block of mass 980 gm suspended by a string. Calculate velocity acquired by the combined system.
Q.26 Due to internal combustion inside a rocket, gases are ejected at the rate of 2.4 kg/minute. The velocity of the gases with respect to the rocket is 400 m/s. Calculate force exerted on the rocket
Q.27 A rifle man, who together with his rifle has a mass of 100 kg, stands on a smooth surface fires 10 shots horizontally. Each bullet has a mass 10 gm a muzzle velocity of 800 m/s.What velocity does rifle man acquire at the end of 10 shots?
Q.28 A body of mass 1 kg strikes elastically with another body at rest and continues to move in the same direction with one fourth of the initial velocity. What will be the mass of the other body
Q.29 A block of mass m1 = 150 kg is at rest on a very long frictionless table, one end of which is terminated in a wall. Another block of mass m2 is placed between the first block and the wall, and set in motion towards m1 with constant speed u2. Assuming that all collisions are completely elastic, find the value of m2 for which both blocks move with the same velocity after m2 has collided once with m1 and once with the wall.
(The wall has effectively infinite mass.)
Q.30 What will be the pressure in N/m2 at a depth of 15cm in brine of density
1.2 gm/cm3 ?
Q.31 Calculate the density of a liquid if the pressure at a pt 30 m below its surface is
32 × 104 N/m2.
Q.32 A force of 150 N is applied on an area of 1.5 m2. Calculate the pressure exerted.
Q.33 A force of 500 dynes is applied on an area of 20 cm2. Calculate the pressure exerted.
Q.34 A body weighs 300 gmf in air and 260 gmf when completely immersed in water. Calculate the following :
(i) loss in weight of the body
(ii) upthrust on the body.
Q.35 A solid block of volume 2 litres has a weight of 80 N. What will be its weight when immersed completely in water ?
Q.36 A solid block of density D has a weight W in air is fully immersed in a liquid of density d. Calculate its apparent weight when fully immersed in liquid.
Q.37 A body weighs 30 N in air and 26 N when fully immersed in water. Calculate its relative density.
Q.38 Relative density of copper is 8.8. What is its density in SI system ?
Q.39 A solid weighs 60 gmf in air and 52 gmf when completely immersed in water. Calculate the following :
(i) upthrust,
(ii) volume of the solid,
(iii) relative density of the solid
Q.40 For determining the relative density of a liquid, following observations are taken. Weight of solid in air = 0.200 kgf; Weight of solid immersed in liquid = 0.160 kgf; Weight of solid in water = 0.0150 kgf. Calculate the following :
(i) Loss of weight of solid in liquid.
(ii) Loss of weight of the solid in water.
(iii) Relative density of the liquid.
Q.41 When a force of 40 N is applied on a body it moves with an acceleration of 5 ms–2. Calculate the mass of the body.
Q.42 It is required to increase the velocity of a scooter of mass 80 kg from 5 to 25 ms–1 in
2 sec. Calculate the force required.
Q.43 Two blocks made of different metals identical in shape and sizes are acted upon by equal forces which cause them to slide on a horizontal surface. The acceleration of the second block is found to be 5 times that of the first. What is the ratio of the mass of the second to the first?
Q.45 An object undergoes an acceleration of 8 ms–2 starting from rest. Find the distance travelled in 1 second.
Q.1 An external influence which changes or tends to change the state of rest or uniform motion of body or its dimensions is called :
(A) momentum (B) force
(C) moment of force (D) pressure
Q.2 Equal and opposite forces acting on a body which do not change its state of rest or uniform motion are called:
(A) like parallel forces (B) unlike parallel forces (C) balanced forces (D) all the above
Q.3 The unequal and opposite forces acting on a body, which change its state of rest or uniform motion are called:
(A) unbalanced forces (B) balanced forces (C) like parallel forces (D) all the above
Q.4 Force of friction always acts in the direction:
(A) of applied force
(B) opposite to the direction of applied force
(C) at right angles to the direction of applied force
(D) none of the above
Q.5 When balanced forces act on a body, the body:
(A) must remain in its state of rest
(B) must continue moving with uniform velocity, if already in motion
(C) must experience some acceleration
(D) both (A) and (B)
Q.6 When unbalanced forces act on a body, the body:
(A) must move with uniform velocity (B) must remain at rest
(C) must experience acceleration
(D) must move in a curved path
Q.7 If no external force acts on a body, it will :
(A) move with more speed
(B) change its shape
(C) break into pieces
(D) either remain in its state of rest or in uniform motion.
Q.8 If a body is allowed ti freely fall from a height, its speed increases continuously. It is because:
(A) air does not exert frictional force
(B) magnetic force of earth increases its speed
(C) gravitational force of earth increases its speed
(D) pressure of air forces it downward
Q.9 A force of magnitude' F' acts on a body of mass 'm'. The acceleration of the body depends upon:
(A) volume of body (B) density of body (C) area of body (D) mass of body
Q.10 Force remaining constant, if the mass of body increases, its acceleration is likely to :
(A) increase (B) remain same
(C) decrease (D) sometimes increases and sometimes decreases
Q.11 A force F produces an acceleration 'a' in a body. The same force produces and acceleration 4a in another body. The mass of other body is :
(A) four times the mass of first body (B) four times less the mass of other body
(C) mass does not play role
(D) none of the above
Q.12 When a running motorbike accelerates suddenly, the pillion rider has a tendency to fall backward. This is an example of:
(A) Newton's first law of motion
(8) Newton's second law of motion
(C) Newton's third law of motion
(D) Newton's law of gravitation of motion
Q.13 Which is the incorrect statement?
A spaceship continues moving in space with uniform speed because:
(A) no force of friction due to air acts on it (B) its mass is zero in space
(C) no force of gravitation acts on it (D) no force of friction due to earth acts on it
Q.14 The impact which a body can produce due to the combined effect of mass and velocity is called:
(A) momentum (B) force
(C) moment of force (D) pressure
Q.15 The SI unit of momentum is :
(A) newton (B) newton-second (C) dyne (D) dyne-second
Q.16 The tendency of a body to continue in its state of rest or uniform motion, even on the application of external force is called:
(A) force (B) momentum (C) inertia (D) impulse
Q.17 A body will continue in its state of rest or uniform motion in a straight line, unless acted by some external force. The statement represents :
(A) Newton's second law of motion
(B) Newton's first law of motion
(C) Newton's third law of motion
(D) Law of conservation of momentum
Q.18 The magnitude of inertia of a body is determined by its:
(A) mass (B) weight
(C) velocity (D) acceleration
Q.19 Momentum is a:
(A) vector quantity
(B) scalar quantity
(C) fundamental quantity
(D) none of the above
Q.20 A body P has mass 2 m and velocity 5 v. Another body Q has mass 8 m and velocity 1.25 v. The ratio of momentum of P and Q is :
(A) 2 : 1 (B) 1 : 1
(C) 1 : 2 (D) 3 : 2
Q.21 The magnitude of a physical quantity is 8.5 Ns. The physical quantity is :
(A) force (B) momentum (C) pressure (D) moment of force
Q.22 There is a rubber ball and a stone ball of same size. If both balls are at rest:
(A) rubber ball has more inertia than stone ball (B) stone ball has more inertia than rubber ball
(C) both have same inertia
(D) none of the above.
Q.23 When we vigorously a shake branch of a tree, some leaves get detached. It is due to the:
(A) inertia of rest
(B) inertia of motion
(C) some leaves are loosely held by the branch (D) none of the above.
Q.24 When the driver of a fast moving car suddenly applies brakes, the passengers in the car:
(A) fall backward (B) fall forward
(C) are not affected (D) none of the above.
Q.25 A batsman hits a cricket ball, which then rolls on a level ground. After covering a short distance, the ball comes to rest. The ball slows down to stop because:
(A) the batsman did not hit the ball hard
(B) velocity of ball is proportional to force acting on it
(C) there is force on the ball opposing its motion
(D) there is no unbalanced force on the ball and hence it comes to rest
Q.26 The force of freely falling body is directly proportional to:
(A) mass of body (B) acceleration of body (C) velocity of body (D) both (A) and (B)
Q.27 The principle of conservation of linear momentum states that in a system it :
(A) cannot be changed
(B) can be changed, if internal forces act on it
(C) can be changed, if external forces act on it (D) none of the above
Q.28 Action-reaction forces:
(A) act on same body
(B) act on different bodies
(C) act along different lines
(D) act in same direction
Q.29 A porter is carrying a weight of 200 N on his head. If the force exerted on his head is taken as action, then the reaction force is exerted by :
(A) the head on the weight
(B) the weight on the earth
(C) the earth on the porter
(D) the earth on the weight
Q.30 Which of the following are vector quantities:
(A) momentum (B) velocity
(C) force (D) all of the above.
Q.31 Two bodies collide at the same time. Which of the following is conserved?
(A) velocity (B) kinetic energy (C) momentum (D) force
Q.32 Impulse is equal to :
(A) the change in force
(B) the change in momentum
(C) the change in velocity
(D) all the above
Q.33 A rocket works on the principle of:
(A) conservation of energy
(B) conservation of linear momentum
(C) conservation of inertia
(D) conservation of force
Q.34 When a speeding car takes a sharp turn, the persons sitting in it experience outward pull. This happens due to:
(A) inertia of direction
(B) change in momentum
(C) change in acceleration
(D) none of the above
Q.35 The ratio of force and acceleration of a moving body is the measure of its:
(A) velocity (B) momentum (C) mass (D) impulse
Q.36 When you kick a stone, you get hurt. Due to which property this happens?
(A) inertia of stone
(B) velocity of the kick
(C) momentum of the kick
(D) reaction of the stone
Q.37 A motor bike accelerates on the horizontal road due to the force exerted by :
(A) the engine of motorbike
(B) the earth
(C) the driver on the motorbike
(D) none of the above.
Q.38 Impulse has same unit as that of:
(A) force (B) pressure
(C) momentum (D) moment of force
Q.39 By Newton's second law, the physical quantity which can be calculated, if we know the magnitude of force on a given mass is :
(A) velocity
(B) acceleration
(C) momentum
(D) none of the above.
Q.40 A body is moving with a constant momentum. The motion of the body is :
(A) uniform velocity
(B) accelerated
(C) de-accelerated
(D) none of the above.
Q.41 A cracker at rest explodes into two equal parts. These parts will move in :
(A) opposite direction with different velocities (B) same direction with different velocities
(C) same direction with same velocities (D) opposite direction with same velocities
Q.42 A batsman has a choice to use heavy or light bat, while facing a fast bowler. He will prefer:
(A) light bat, because handling it is easy (B) heavy bat, so that he can handle it firmly
(C) heavy bat, because it will recoilless (D) none of the above.
Q.43 A vehicle has a mass of 1500 kg. If the vehicle is to be stopped with a negative acceleration of 1.7 ms–2, the force of friction between the vehicle and road is :
(A) –2250 N (B) –2050 N
(C) –2550 N (D) none of the above.
Q.44 A man while running at a constant acceleration of 3.5 ms–2, develops a force of 280 N. The mass of man is:
(A) 80 kg (B) 85 kg
(C) 75 kg (D) 60 kg
1. B 2. C 3. A 4. B 5. D 6. C 7. D 8. C 9. D 10. C
11. B 12. A13. B 14. A 15. B 16. C 17. B 18. A 19. A 20. B
21. B 22. B 23. A 24. B25. C 26. D 27. A 28. B 29. C 30. D
31. C 32. B 33. B 34. A 35. C 36. D 37. B 38. C 39. B 40. D 41. D 42. C 43. C 44. A
· Fill in the blanks
1. The forces of action and reaction have ___________ magnitudes but ___________ directions.
2. A body kept at rest will remain ___________ if no unbalanced force acts on it.
3. The linear momentum of a system remains constant if no___________ force acts on it.
1. A force of 100 N acts on 50 kg for 2 seconds. The same force acts on 25 kgs for 2 seconds. The ratio of the momenta produced and the accelerations caused in two bodies respectively are –
(A) 1 : 1, 2 : 1 (B) 1 : 1, 1 : 2 (C) 1 : 2, 1 : 1 (D) none of these
2. The driver of a three-wheeler moving with a speed of 36 km/h sees a child standing in the middle of the road and brings his vehicle to rest in 4.0 s just in time to save the child. The average retarding force on the vehicle? The mass of the three-wheeler is 335 kg and mass of the driver is 65 kg.
(A) 1025 N (B) 10 N (C) 1000 N (D) none of these
3. A shell of mass 0.020 kg is fired by a gun of mass 100 kg. If the muzzle speed of the shell is 80 m/s, the recoil speed of the gun –
(A) 14 m/s (B) 0.012 m/s (c) 0.016 m/s (D) 100 m/s
4. A horizontal force of 600 N pulls two masses 10 kg and 20 kg (lying on a frictionless table) connected by a light string. The tension in the string , if the 20 kg mass is pulled
(A) 200 N (B) 400 N (C) 100 N (D) 50 N
5. Two masses 8 kg and 12 kg are connected at the two ends of a light inextensible string that goes over a frictionless pulley. The acceleration of the masses, when the masses are released is (g = 10 m/s2)
(A) 6 m/s2 (B) 4 m/s2 (C) 10 m/s2 (D) 2 m/s2
6. Two billiard balls each of mass 0.05 kg moving in opposite directions with speed 6 m/s collide and rebound with the same speed. The magnitude of impulse imparted to each ball due to the other –
(A) 0.6 kg m/s (B) zero (C) 6 kg m/s (D) none of these
Instructions: In the following questions as Assertion (A) is given followed by a Reason (R). Mark your responses from the following options.
(A) Both Assertion and Reason are true and Reason is the correct explanation of ‘Assertion’
(B) Both Assertion and Reason are true and Reason is not the correct explanation of ‘Assertion’
(C) Assertion is true but Reason is false
(D) Assertion is false but Reason is true
1. Assertion: Large force is required to move a body uniformly along a straight path
Reason: A body moving with uniform acceleration has a constant force acting on it.
2. Assertion: Linear momentum of a body changes when the body is moving in a circle.
Reason: In uniform circular motion the velocity changes because of change in direction.
3. Assertion: A player lowers his hands while catching a ball.
Reason: Impulse is the time rate of change of momentum.
4. Assertion: Mass is a measure of inertia of the body in linear motion.
Reason: Smaller the mass, smaller is the force required to change its state.
Column-I and column-II contains four entries each. Entries of column-I are to be matched with some entries of column-II. Only One entries of column-I may have the matching with the same entries of column-II and one entry of column-II Only one matching with entries of column-I
1. Column I Column II
(A) Measure of inertia (P) Force × time
(B) Impulse (Q) Mass × velocity
(C) Momentum (R) Mass × acceleration
(D) Newton’s second law of motion (S) Mass
· Multiple choice question with one correct answers
1. If a body is in equilibrium under a set of non-collinear forces, the minimum number of forces has to be:
(A) Four (B) Three (C) Two (D) Five
2. Bullets of 0.03 kg mass each hit a plate at the rate of 200 bullets per second, with a velocity of 50 m/sec. reflect back with a velocity of 30 m/sec. The average force acting on the plate, in newtons is:
(A) 120 (B) 180 (C) 300 (D) 480
3. A force of 5 N making an angle q with the horizontal acting on an object displaces it by 0.4 m along the horizontal direction.If the object gains kinetic energy of 1 J, the horizontal component of the force is:
(A) 1.5 N (B) 2.5 N (C) 3.5 N (D) 4.5 N
4. A force of 50 dynes is acted on a body of mass 5g which is at rest for an interval of 3sec. The impluse is
(A) 0.15 × 10–3 Ns (B) 0.98 × 10–3 Ns (C) 1.5 × 10–3 N.s (D) 2.5 × 10–3
5. Swimming is possible by the:
(A) first law of motion (B) second law of motion
(C) third law of motion (D) Newtons law of gravition
6. A cricket player catches a ball of mass 0.1 kg, moving with a speed 10 m/s in 0.1 second. Froce exerted by him is (N)
(A) 4 (B) 2 (C) 1 (D) 10
1. Newton’s first law of motion defines
(A) Force (B) Inertia (C) Momentum (D) Acceleration
2. Which of the following statements is/are not correct ?
(A) A force is needed to keep a particle moving along a straight line with uniform velocity.
(B) The same force for the same time causes the same change in momentum for different bodies.
(C) Frictional force opposes both motion as well as relative motion.
(D) It is not motion, but relative motion that the frictional force opposes.
3. Which of the following statements is/are correct ?
(A) Momentum has both direction and magnitude
(B) Momentum is a scalar quantity
(C) The SI unit of momentum is kilogram-metre per second.
(D) The rate of change of momentum of an object is in the direction of force.
4. Action-Reaction forces act
(A) on the same body (B) on the different bodies
(C) along the same lines (D) in the same direction
5. A constant force acts on an object of mass 4 kg for a duration of 1 second. It increases the object velocity from 4 ms–1 to 6 ms–1. Select the correct options.
(A) Magnitude of the applied force is 8 N
(B) Final velocity of the object if the force applied for 5 sec is 24 m/s
(C) Change in momentum in 1 sec is 8 kg m sec–1
(D) Change in momentum of object during 5 sec is 56 kg m/sec
6. A girl of mass 30 kg jumps with a horizontal velocity of 4 m sec–1 onto a stationary cart with frictionless wheels. The mass of cart is 2 kg. Select the correct options
(Assuming that there is no external unbalanced force working in the horizontal direction)
(A) The total momentum of the girl and the cart before the interaction is 120 kg m sec–1
(B) The total momentumof the girl and the cart after the interaction is 120 kg m sec–1
(C) The girl on cart will move with a velocity 15 m sec–1 in the direction in which the girl jumped
(D) The girl on cart will move with a velocity 15/4 m sec–1 in the opposite direction in which the girl jumped
A truck is hauling a trailer along a level road as figure illustrates. The mass of the truck is m1 = 8500 kg and that of the trailer is m2 = 27000 kg.
The two move with an acceleration of a = 0.78 m/s2. Ignore the retarding forces of friction and air resistances.
1. The magnitude of the tension in the horizontal drawbar between the trailer and the truck
(A) 21000 N (B) 28000 N (C) 60000 N (D) None of these
2. The force D that propels the truck forward
(A) 21000 N (B) 28000 N (C) 60000 N (D) None of these
3. The action and reaction forces are
(A) D and T (B) T and T´ (C) D and T´ (D) None of these
· Match the following (one to many)
Column-I and column-II contains four entries each. Entries of column-I are to be matched with some entries of column-II. One or more than one entries of column-I may have the matching with the some entries of column-II and one entry of column-II may have one or more than one matching with entries of column-I
1. Column I Column II
(A) A rocket works on the principle of (P) First law of motion
(B) Recoiling of gun can be explained by (Q) Second law of motion
(C) The law which defines the force is (R) Third law of motion
(D) The law which gives the quantitative (S) Conservation of momentum
measurement of force is
Section-A
1. Equal, Opposite 2. At rest 3. Unbalanced
Section-B
1. (B) 2. (C) 3. (C) 4. (A)
5. (D) 6. (A)
Section-C
1. (D) 2. (A) 3. (C) 4. (A)
Section-D
1. (A)-(S), (B)-(P), (C)-(Q), (D)-(R)
Section-A
1. (B) 2. (D) 3. (B) 4. (C) 5. (C)
6. (D)
Section-B
1. (A,B) 2. (A,C) 3. (A,C,D) 4. (B,C) 5. (A,C)
6. (A,B)
Section-C
1. (A) 2. (B) 3. (B)
Section-D
1. (A)- (R,S), (B)-(R,S), (C)-(P), (D)-(Q)