FUELS
A combustible substance which on burning produces a large amount of heat and light is called a fuel.
Coal, LPG, Petrol, Kerosene, wood etc.
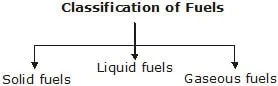
Classification of Fuels
Fuels are classified on the basis of physical state in which they occur. So fuels are classified as solid, liquid and gaseous fuels.
(i) Solid fuels : Combustible substances which are solid at room temperature are called solid fuels. Solid fuels contain mainly carbon both as free and combined carbon. In rural areas, Firewood, Agricultural wastes, Animal-dung cakes are the major source of energy.
Examples : Some solid fuels are :
(a) Coal (b) Coke (c) Wood (d) Charcoal
(e) Animal-dung cakes (f) Agricultural wastes
(ii) Liquid fuels : Volatile liquids which produce combustible vapour are called liquid fuels. Kerosene is the most commonly used liquid fuel.
Examples : Some common liquid fuels are :
(a) Petrol (b) Diesel (c) Kerosene (d) Alcohol
Petrol, diesel and kerosene are mixtures of hydrocarbons.
(iii) Gaseous fuels : Combustible gases or mixtures of combustible gases are called gaseous fuels.
Examples : Some commonly used gaseous fuels are :
(a) Natural gas (b) Liquified petroleum gas (LPG)
(c) Biogas (or Gobar gas) (d) Coal gas
(e) Water gas (f) Producer gas
(g) Hydrogen gas (h) Compressed Natural (CNG)
Petroleum gas is obtained as a by-product during the fractional distillation of petroleum.
I. CHARACTERISTICS OF AN IDEAL FUEL:
An ideal fuel should have the following characteristics :
(i) It should be fairly cheap and easily available.
(ii) It should burn at moderate rate.
(iii) It should not produce any poisonous and irritating fumes during burning.
(iv) It should leave no residue (ash) after burning.
(v) It should produce large amount of heat per unit mass i.e., it should have high calorific value.
(vi) It should be safe and convenient from the storage and transportation point of views.
(vii) Its ignition temperature should be above room temperature. So that it is safe to use such as a fuel.
II. USES OF FUELS:
(i) Cooking and Heating : The most common use of fuels is for cooking and heating. The commonly used domestic fuels are wood, dry cattle dung, coal, charcoal, kerosene (in rural areas) and coal, kerosene, LPG (in urban areas).
(ii) For Transportation : Fuels such as petrol, diesel and CNG are used for running cars, scooters, buses, trucks and trains. These automobiles are used for transportation from one place to another. The fuel used in aeroplanes is called aviation fuel.
(iii) For Generating Electricity : Fuels such as coal and natural gas are used for generating electricity on a commercial scale, in Thermal power stations. Petrol, diesel and kerosene are also used for generating electricity in smaller generators commonly used at homes and shops, etc.
(iv) In Industry : Fuels such as coal, natural gas, diesel and furnace oil are used in the industry for generating steam in boilers. Steam is required in industry for heating purposes and also for generating electricity for their own use in factory. Industry in the rural areas also uses biomass such as bagasse—the cellulose material left after extracting juice from the sugarcane for running boilers.
(v) For Launching Space Vehicles : Space vehicles are launched with the help of rockets. Rockets use special fuels called propellants. A propellant is a combination of a fuel and an oxidizer.
COAL
III. INTRODUCTION
Coal is a mineral of dark brown or black colour formed from the remains of plants buried in the earth’s crust millions of years ago.
IV. COMPOSITION:
Coal is a very impure form of carbon. It mainly consists of atoms of carbon, hydrogen and oxygen. A small amount of sulphur is also present in it.
V. MINING
Coal is mined using two methods–opencast mining and underground mining. Opencast mining is used when the deposits of coal are near the surface of the earth. Underground mining is used when coal deposits lie deep inside the earth’s crust.
VI. FORMATION
Coal is formed from vegitation matter burried under the earth. About 300 million years ago, the earth was covered with dense forests, marshlands and rivers. The forests grew and died and fell into the waters of the surrounding swamps. These plants were covered with tons of earth over a period of millions of years. Due to the huge pressure and temperature inside the earth, this vegitation matter got converted into coal. For this reason, coal is known as fossil fuel. It is also a non-renewable source of energy.
VII. TYPES OF COAL:
Coal comes in four main varieties. The percentage of carbon in air-dried samples are as follows.
(i) Peat : This is a material in the first stage of coal formation. It contains only 27% carbon and is considered to be the lowest grade of coal.
(ii) Lignite : This variety of coal contains 28-30% carbon. It has poor heating power. It is brown in colour but lustrous when dry.
(iii) Bituminous : It is a soft coal containing 78-86% carbon. It gives a large proportion of gas when heated and burns with a yellow, luminous flame.
(iv) Anthracite : It is a hard coal and contains 94-98% carbon. It is lustrous. It burns without smoke and gives much heat and little ash.
Bituminous coal is by far the most useful as a fuel, but anthracite is considered to be the most superior in quality.
VIII. USES:
(i) Coal is used as a fuel to convert water into steam to run thermal power plants for the generation of electricity. It is also used as a fuel in homes and factories, and to run steam engines.
(ii) Coal is used in the preparation of fuel gases, such as coal gas.
(iii) Coal is used in the preparation of synthetic oil and synthetic natural gas.
(iv) Coal is also used to obtain natural gas. For this, finely grinded coal is heated with hydrogen under pressure in the presence of a suitable catalyst. The complex molecules present in coal combine with
(v) The destructive distillation of coal gives coke, coal tar, coal gas, etc.
(vi) Coal is the source from which a number of organic compounds such as benzene, toluene, phenol, naphthalene and anthracene are obtained.
Destructive Distillation of Coal
The process of destructive distillation is carried out be heating coal at a high temperature
(1270 K) in the absence of air. This process is also called as pyrolysis and yields lot of valuable products.
(i) Products of destructive distillation of coal
(a) Coke (B) Coal Tar (C) Ammoniacal liquor (D) Coal gas
(ii) Coke : Solid residue left after destructive distillation (high percentage carbon-nearly 98%)
(iii) Uses :
(i) As domestic fuel.
(ii) Acts as a good reducing agent in the manufacture of steel
(iii) Useful fuel gases like water gas and producer gases can be made using coke.
5 Water gas is a mixture of carbon monoxide and hydrogen. It is obtained by passing steam over red-hot coke.
C + H2O ---> CO + H2
5 Producer gas is a mixture of carbon monoxide and nitrogen. It is obtained when air is passed over red-hot coke.
2C + O2 + 4N2 ---> 2CO + 4N2
(iv) Used in metallurgical operations as a reducer for oxide ores.
(v) Coal Tar : Coal tar is a mixture of different carbon compounds. It is a thick, black liquid. The fractional distillation of coal tar gives many chemical substances which are used in the preparation of dyes, explosives, paints, synthetic fibres, drugs and pesticides. Some of these chemical substances are benzene, toluene, phenol and aniline.
(vi) Ammoniacal Liquor : The ammonia produced as a result of destrutive distillation of coal is absorbed in water. The aqueous solution of ammonia, i.e., ammonium hydroxide solution, is called ammoniacal liquor. It is used in the preparation of fertilizers such as ammonium sulphate and ammonium superphosphate.
NH3 + H2O ---> NH4OH
2 NH4OH + H2SO4 ---> (NH4)2SO4 + H2O
Coal Gas : Coal gas is a mixture of hydrogen, methane and carbon monoxide. The gases present in coal gas are combustible, and hence it is an excellent fuel. It has a high calorific value. It was used for lighting houses, factories and streets in Mumbai until 1950. It was also used for cooking until recently.
PETROLEUM
Petroleum is a naturally occurring oil that consists chiefly of hydrocarbons with some other elements, such as sulphur, oxygen and nitrogen. It is now known that petroleum contains hydrocarbons of the paraffin series, with upto 100 or more carbon atom s in the chain. The unrefined form of petroleum is called crude oil or rock oil (petra = rock; oleum = oil).
IX. ORIGIN OF PETROLEUM:
Petroleum was formed from organisms living in the sea. The remains of these organisms were deposited in shallow depressions in the sea bed long, long ago. These were covered by layers of sand and clay which compressed these remains. Over a period of millions of years, the organic matter present in the dead organisms underwent a series of processes before being finally transformed into petroleum. The petroleum migrated from the source rock to be entrapped in large underground reservoirs beneath impermeable rocks. It often floats over a layer of water and is held in this position under pressure beneath a layer of natural gas.
X. OIL WELLS IN INDIA:
In India, oil was first struck at Makum in Assam in 1867. The oil fields of Assam were the only source of petroleum in our country until about 40 years ago. Some other places in our country where oil wells have been dug are
(i) Ankleshwar and Kalol in Gujarat,
(ii) Offshore areas west of Mumbai, and
(iii) Offshore deltas of the Godavari and Kaveri rivers.
There are some government agencies engaged in exploring and producing crude oil-Oil and Natural Gas Commission (ONGC) and Oil India Limited (Oil). There are many refineries in India. The larger refineries are at Jamnagar, Mathura, Bharuch, Digboi, Haldia and Barauni.
Refining
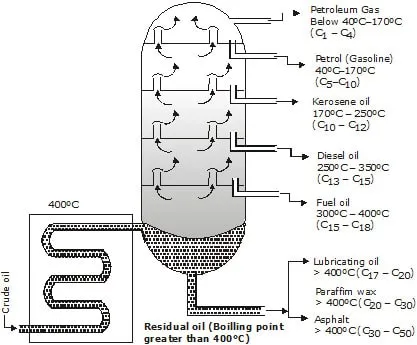
The process of separating the various components of petroleum from one another is known as the refining of petroleum. This is done by a process called fractional distillation which is based on the fact that the different components of petroleum have distinctly different boiling points.
XI. PRODUCTS OF PETROLEUM REFINING:
(i) Asphalt : Asphalt is a black and sticky substance. It is used for making the surface of roads. It does not burn readily.
(ii) Paraffin Wax : It boils at above 673 K. It is obtained by the fractionation of residual oil. It is used for making candles, vaseline, grease, polishes, etc.
(iii) Lubricating Oil : It boils at well above 673 K. It is obtained by the fractionation of residual oil. It is used for lubricating machinery.
(vi) Fuel Oil : The boiling range of fuel oil is 623 K to 673 K. It is used in industries to heat boilers and furnaces. It is a better fuel than coal because it burns completely leaving behind no ash, whereas coal burns producing a large amount of ash which has to be removed regularly.
(v) Diesel Oil : Its boiling range is 573 K to 623 K. It contains straight-chain alkanes with the number of carbon atoms varying from 20 to 25. It is used in cars, trucks, buses, and locomotives.
(vi) Kerosene : Its boiling ranges is 443 K to 523 K. It contains straight-chain alkanes with 10-16 carbon atoms. It is used for domestic purposes, for lighting petromax, lanterns, lamps, stoves, etc.
(vii) Petrol : Its boiling range is 313 K to 443 K. It is also called gasoline. it contains paraffins from pentane to do decane. It is used as a fuel in two-wheelers, three-wheelers and cars.
(viii) Residual Oil : The residual oil obtained from the primary distillation of petroleum is known as reduced crude. Reduced crude is distilled in vacuum to yield bitumen as residue. Bitumen is largely used in making road surfaces, and also for coating cables to provide electrical insulation.
XII. USES:
(i) Petroleum gas is used as a fuel. It is also used in the form of liquefied petroleum gas (LPG) for domestic purposes.
(ii) Gasoline or petrol is used as a fuel in cars, scooters, etc.
(iii) Kerosene is used as a household fuel.
(iv) Diesel oil is used as a furnace fuel and fuel for diesel engines.
(v) Lubricating oil is used for lubrication of machinery, etc.
(vi) Vaseline is used for softening skin.
(vii) Paraffin wax is used for making candles
(viii) Most industrial chemicals are produced from petroleum and natural gas. These chemicals are called petrochemicals. Petroleum is the major source of medicines, insecticides, rubbers, plastics, perfumes, explosives, motor fuels, etc.
(ix) Petroleum Gas : It is a mixture of ethane, propane and butane. Its main constituent is butane which burns giving off a lot of heat. Butane is easily liquefied under high pressure. In the liquid form it is supplied in cylinders and is commonly known as Liquefied Petroleum Gas (LPG).
(x) Liquefied Petroleum Gas (LPG) :
Liquefied petroleum gas is petroleum gas in liquid state. It is a mixture of ethane, propane and butane, but the major component is butane.
LPG is a colourless, odourless (when pure) gas. The commercially supplied LPG contains a strong smelling compound called ethyl mercaption (C2H5SH) to permit its detection in the case of any leakage.
SOLVED EXAMPLES
Ex.1 What are the advantages of using CNG and LPG as fuels?
Sol. The advantages of using CNG and LPG as fuel are :
(i) A non-polluting fuel for vehicles. (ii) It is used for power generation.
(iii) It can be used directly for burning in homes and factories.
Ex.2 Name the petroleum product used for surfacing of roads :
Sol. A petroleum product 'Bitumen' is used for surfacing of roads.
Ex.3 Describe how coal is formed from dead vegetation. What is the process called?
Sol. About 300 million years ago the earth had dense forests in low lying wetland areas. Due to natural process, like flooding, these forests got buried under the soil. As more soil deposit over them, they were compressed. The temperature also rose as they sank deeper and deeper. Under high pressure and high temperature, dead plants got slowly converted to coal.
As coal contains mainly carbon, the slow process of conversion of dead vegetation into coal is called carbonisation.
Ex.4 Fill in the blanks :
(a) Fossil fuels are ...........,........... and ...........
(b) Process of separation of different constituents from petroleum is called ...........
(c) Least polluting fuel for vehicle is ...........
Sol. (a) Coal, petroleum, natural gas (b) Refining (c) CNG.
Ex.5 Tick True/False against the following statements :
(a) Fossil fuels can be made in the laboratory (b) CNG is more polluting fuel than petrol.
(c) Coke is almost pure form of carbon. (d) Coal tar is a mixture of various substances.
(e) Kerosene is not a fossil fuel.
Sol. (a) False (b) False (c) True (d) False (e) False
Ex.6 Describe characteristics and uses of coke :
Sol. It is a tough, porous and black substances. It is almost pure form of carbon. "Coke is obtained by heating soft coal in the absence or little supply of air".
It is used in the manufacture of steel and in the extraction of many metals.
Ex.7 Explain the process of formation of petroleum :
Sol. Petroleum occurs deep down in the earth between layers of non-porous rocks. Crude oil petroleum is formed by the decomposition of animal and plant remains over millions of years inside the earth. Natural gas occurs above the petroleum oil trapped under the rocks.
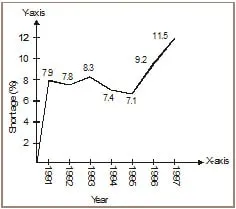
Ex.8 The following table shows the total power shortage in India from 1991-1997. Show the data in the form of a graph. Plot shortage percentage for the years on the Y-axis and the year on the X-axis:

Sol.
EXERCISE -I
Q.1 Name any two products of petroleum refining.
Q.2 Name the petroleum product used for surfacing of roads.
Q.3 How is coke obtained
Q.4 Name the purest form of carbon.
Q.5 How is coal tar formed ?
Q.6 Give the main use of coal gas.
Q.7 How is petroleum formed ?
Q.8 Why is petroleum called a fossil fuel ?
Q.9 What is meant by refining of petroleum ?
Q.10 Where is petroleum found in India ?
Q.11 Name the fraction of petroleum used for making ointments and candles.
Q.12 Expand CNG.
Q.13 Name two fuels which are used for running automobiles.
Q.14 Why is food regarded as a fuel for our body?
Q.15 Name a liquid fuel which is used in homes?
Q.16 Write the full forms of (a) CNG (b) LPG
Q.17 Give two characteristics of coal.
Q.18 Give two use of coke.
Q.19 Why should the fossil fuels be used with care
Q.20 (a) Name the products obtained when coal is heated in the absence of air.
(b) Write any two uses of its products.
Q.21 How is 'petrol' related to 'petroleum' ? Name four most important products obtained from petroleum.
Q.22 Give reasons –
(i) LPG is a better domestic fuel than wood.
(ii) Water is not used to control fires involving electrical equipment.
Q.23 Differentiate between inexhaustible and exhaustible natural resources.
Q.24 Give the uses of the following
(i) coke (ii) coal tar (iii) coal gas
Q.25 Write a short note on the formation of coal.
Q.26 Give the uses of the following :
(i) Kerosene (ii) Lubricating oil
(iii) Paraffin wax (iv) Diesel
EXERCISE -II
Q.1 Which of the following gases remains liquid at – 88°C?
(A) Ethane and methane
(B) Ethane and propane
(C) Propane and butane
(D) Butane and ethane
Q.2 If 20 ml of Petroleum is heated upto 250°C and gases formed were allowed to pass through a column to cool down upto 130°C. The liquid collected should mainly be a mixture of
(A) Petrol and fuel oil
(B) Petrol and ethanol
(C) Kerosene and fuel oil
(D) Kerosene and naphtha
Q.3 Hydrocarbons contain :
(A) Carbon and hydrogen
(B) Carbon and oxygen
(C) Carbon and nitrogen
(D) Carbon and carbon dioxide
Q.4 Natural gas mainly contains :
(A) Propane (B) Butane
(C) Methane (D) Ethane
Q.5 In the laboratory, methane is prepared by heating a mixture of :
(A) Sodium acetate and sodium carbonate (B) Sodium acetate and soda lime
(C) Soda lime and sodium hydroxide
(D) Soda lime and calcium oxide
Q.6 Which of the following is known as 'Fire damp' in coal mines?
(A) Ethanol (B) Carbon monoxide (C) Carbon dioxide (D) Methane
Q.7 Which of the following gases can be liquefied under pressure?
(A) Propane and Methane
(B) Methane and Ethane
(C) Butane and Propane
(D) Butane and Methane
Q.8 Which of the following gases is supplied in LPG (Liquefied Petroleum Gas) cylinders for domestic use?
(A) Methane and Propane
(B) Methane and Ethane
(C) Ethane and Butane
(D) Propane and Butane
Q.9 55000 kilo joule/kg heat value is present in :
(A) Methane (B) Ethane
(C) Propane (D) Butane
Q.10 How many carbon atoms are present in one molecule of liquid hydrocarbon?
(A) 5 (B) 4
(C) 3 (D) 6 or more
Q.11 Petroleum is refined by :
(A) Simple distillation
(B) Fractional distillation
(C) Destructive distillation
(D) None of the these
Q.12 Power alcohol is :
(A) Alcohol mixed with petrol
(B) Alcohol mixed with kerosene
(C) Alcohol mixed with sulphur
(D) Alcohol mixed with ethane
Q.13 Water gas contains :
(A) Hydrogen and carbon dioxide
(B) Hydrogen and nitrogen
(C) Hydrogen and carbon monoxide
(D) None of these
Q.14 Producer gas contains
(A) Nitrogen and carbon monoxide
(B) Hydrogen and nitrogen
(C) Nitrogen and carbon dioxide
(D) Hydrogen and carbon dioxide
Q.15 Coal gas mainly contains :
(A) Hydrogen, methane and carbon dioxide (B) Hydrogen, methane and nitrogen
(C) Methane and nitrogen
(D) Hydrogen, methane and carbon monoxide
Q.16 Naphtha is used in :
(A) Jet engine
(B) Lubrication
(C) Automobile engines
(D) Petrochemicals
Q.17 The burning of kerosene in stove is called :
(A) Spontaneous combustion
(B) Rapid combustion
(C) Slow combustion
(D) None of these
Q.18 Oldest form of fossil coal is :
(A) Lignite (B) Anthracite
(C) Coke (D) Charcoal
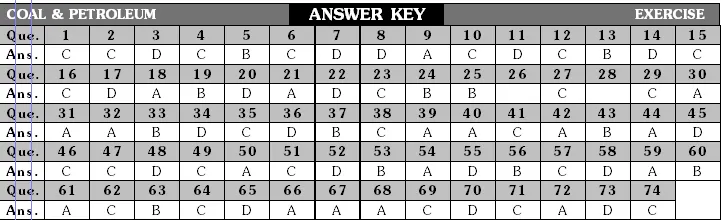
ANSWERS KEYS
1. C 2. C 3. A 4. C
5. B 6. D 7. C 8. D
9. A 10. D 11. B 12. A
13. C 14. A 15. D 16. D
17. A 18. B
EXERCISE - III
1. Kerosene oil is a mixture of hydrocarbons containing number of carbon atoms -
(A) C6 to C10 (B) C8 to C12 (C) C11to C16 (D) C18 to C22
2. The distillation of crude petroleum to obtain various commercially useful fraction is called
(A) cracking (B) hydroforming (C) refining (D) mining
3. Which of the following is used for refining of petroleum ?
(A) Steam distillation (B) Distillation under reduced pressure
(C) Solvent extraction (D) Fractional distillation
4. Which of the following is properly matched ?
(A) Kerosene – C5 – C10 (B) Diesel oil – C5 – C6
(C) Petrol – C7 – C9 (D) All are correct
5. Which of the following names represents the foul smelling, black, thick, viscous liquid obtained from destructive distillation of coal
(A) Coke (B) Coal tar (C) Coal gas (D) None of these
6. Main constituents of coal gas are :
(A) H2O, C2H6, O2 (B) CH4, CO2, O2 (C) CH4, H2, CO (D) C2H6, N2, O2
7. Which one of the following is not a petroleum product ?
(A) Kerosene (B) Gasoline (C) Pitch black (D) Bees wax
8. Percentage of carbon present in an air dried sample of Anthracite is :
(A) 94 – 98% (B) 27 – 30% (C) 78 – 86% (D) 27 %
9. Ammoniacal liquor is -
(A) ammonia absorbed in water (B) ammonium hydroxide
(C) aqueous solution of ammonia (D) All of the above
10. Which of the following products obtained by destructive distillation of coal, is not properly matched ?
(A) Coal tar – Dyes, explosives, paints (B) Coal gas – Fuel
(C) Coke – Drinking purposes (D) Ammoniacal liquor – Fertilizers
11. Which of the following is known as regenerated fibre ?
(A) Nylon – 66 (B) Terylene (C) Nylon – 6 (D) Rayon
12. Which of the following is a thermosetting plastic ?
(A) PVC (B) Polyethylene (C) Bakelite (D) Terylene
13. The monomer units of neoprene ar known as
(A) isoprene (B) chloroprene (C) vinyl chloride (D) ethylene glycol.
14. The following are synthetic polymers except
(A) teflon (B) terylene (C) nylon (D) proteins
15. The structure of isoprene is -
(A) CH2 = C(C2H5) – CH = CH2 (B) CH2 = C(OCOCH) – CH = CH2
(C) CH2 = C(CH3) – CH = CH2 (D) CH2 = CH – C º CH
16. All are natural fibres except -
(A) silk (B) cotton (C) nylon (D) wool
17. The first man – made polymer is -
(A) PVC (B) Teflon (C) Bakelite (D) Nylon
18. Pick out the incorrect statement amongst the following :
(A) Nylon clothings can with stand high temperature & are therefore, good to wear in summers.
(B) Thermosetting plastics do not become soft on heating.
(C) Addition polymers are formed without the elimination of by- product molecules.
(D) Natural rubber is obtained as latex from rubber trees.
19. Which one of the following is a condensation polymer?
(A) Polyethene (B) Polyester (C) Polystyrene (D) Polypropylene
20. Which one of the following polymers is not properly matched to its monomer ?
(A) Orlon – Acrylonirtile
(B) Synthetic rubber – 2 – Chlorobuta – 1, 3 – diene.
(C) Nylon – Adipic acid & Hexamethylene diamine
(D) Teflon – Vinyl chloride
21. Which of the following is an example of Freon
(A) CCl2F2 (B) CCl4 (C) CHCI3 (D) CH3Cl
22. Pesticides & insecticides are available in the form of
(A) powders (B) sprays (C) emulsions (D) all of these
23. Which of the following statements about 'selphos' is incorrect ?
(A) It is a stomach poison (B) It is used for storage of wheat
(C) It emits chlorine gas (D) It acts as a pesticide
24. Which of the following is a contact poison?
(A) Mercury tablets (B) DDT (C) Cryolite (D) Lead arsenate.
25. LPG mainly contains -
(A) methane & isobutane (B) Propane & butane
(C) ethane & hydrogen (D) hydrsogen & methane
26. What contituents is obtained in the temperature range 175°C – 275°C during the fractional distillation of petroleum -
(A) Gas (B) Gasoline (C) Kerosene (D) Diesel oil
27. The range of number of atoms in the kerosene fraction is -
(A) C1 to C7 (B) C5 to C12 (C) C1 to C16 (D) C15 to C18
28. During the fractional distillation of petroleum, lubricating oil, vaseline and parafin wax is obtained in the temperature range of
(A) 30°C–200°C (B) 175°C – 275°C (C) 250°C – 400°C (D) 350°C and above
29. The main constituents of LPG is -
(A) Methane (B) Propane (C) Butane (D) Pentane
30. Which of the following gas has the highest calorific value -
(A) Hydrogen (B) Methane (C) Butane (D) Biogas
31. Which of the following states produces petroleum from off-shore wells ?
(A) Assam (B) Gujrat (C) Maharashtra (D) West Bengal
32. Which of the following fuel is highly poisonous
(A) Coal gas (B) Charcoal (C) Coke (D) Wax
33. Which of the following coals has the highest carbon content-
(A) Lignite (B) Anthracite (C) Bituminous (D) Peat
34. Which of the following is not obtained in the destructive distillation of coal -
(A) Coal gas (B) Coal tar (C) Ammonia (D) Nitrogen
35. The main constituents of natural gas is -
(A) Methane (B) Ethane (C) Butane (D) Hydrogen
36. The abbreviation LPG stands for -
(A) Liquid petrol gas
(B) Low power gas
(C) Liquefied power gas (D) Liquefied petroleum gas
37. The most common sources of energy are-
(A) Wood and coal (B) Petroleum and coal (C) LPG and cow dung (D) Natural gas and coal
38. When an oil well is drilled through rocks which of the following comes out first -
(A) Coal gas (B) marsh gas (C) natural gas (D) gas carbon
39. Petroleum is refined by
(A) Fractional distillation
(B) Destructive distillation (C) Distillation (D) All of these
40. Which of the following is of fossil fuel
(A) Petroleum (B) Wood (C) Cow dung (D) Dry leaves
41. Which among the following is a dark coloured, viscous, strong smelling liquid -
(A) Kerosene (B) Petrol (C) Petroleum (D) Alcohol
42. Natural gas occurs
(A) Above the petroleum oil
(B) Below the petroleum oil
(C) Along with the petroleum oil (D) None of these
43. Crude oil is a complex mixture of
(A) Solid hydrocarbons
(B) Liquid hydrocarbons (C) Gaseous hydrocarbons (D) All of these
44. Petroleum is commonly called as -
(A) Black gold (B) Yellow gold (C) Green gold (D) Blue gold
45. What should be the characteristic for a rocket fuel-
(A) Light and compact
(B) High calorific value (C) Should burn rapidly (D) All of the above
46. The combustion in a match stick is started by this chemical -
(A) Antimony sulphide
(B) Potassium chlorate (C) Phosphorous
(D) Starch and wool
47. Mixture of carbon monoxide and nitrogen
(A) Coal gas (B) Oil gas (C) Producer (D) Water gas
48. Which of the following gases is essentially a mixture of carbon monoxide and hydrogen
(A) Coal gas (B) Oil gas (C) Producer gas (D) Water gas
49. Natural gas is largely a mixture of -
(A) CO and N2 (B) CO and H2 (C) Methane and CO2 (D) Hydrocarbons
50. Which of the following gaseous fuels is obtained by dry distillation of coal -
(A) Coal gas (B) Oil gas (C) Producer gas (D) Water gas
51. Biogas is obtained from
(A) Wood (B) Charcoal (C) Dung (D) Petrol
52. Which of the following is a better fuel -
(A) Charcoal (B) Wood (C) Dung cake (D) L.P.G.
53. Anaerobic fermentation is a process which helps in formation of -
(A) CO
(B) CO2
(C) Oxides of nitrogen (D) Lead compounds
54. Coal was formed millions of years ago by the decomposition of plants and trees that once grew over the surface ofthe earth. During certain periods violent changes took place on the earth. As a result ground was covered with sand, clay rocky material and water. Inside the earth , these plants and trees were subjected to high temperature and pressure. Chemical changes took place which converted plant matter into coal. This process is known as -
(A) Carbonization (B) Catenation (C) Polymerization (D) Vulcanization
55. Dry distillation of coal gives many valuable and important products. The solid residue left behind after dry distillation of coal is called -
(A) Asphalt (B) Coal pitch (C) Coal tar (D) coke
56. Which of the following statements about petroleum is not correct
(A) Petroleum is a dark coloured oily liquid with a characteristic smell
(B) Petroleum is heavier than water
(C) Petroleum is insoluble in water
(D) Petroleum is formed by decomposition of animal and plant remains inside the earth
57. Petroleum, a crude oil, is a complex mixture of substances. It is refined by the process called
(A) Decomposition
(B) Evaporation
(C) Fractional distillation (D) Sublimation
58. --------has the lowest percentage of carbon
(A) Lignite (B) Bituminous (C) Anthracite (D) Peat
59. -------has the highest percentage of carbon
(A) Anthracite (B) Bituminous (C) Peat (D) Lignite
60. ----------is the common vareity of coal used in household-
(A) Anthracite (B) Bituminous (C) Peat (D) Lignite
61. Fuels burn to produce heat, light and -------
(A) CO2 + water vapour
(B) CO + O2
(C) CO2 + H2 (D) CO + H2
62. The hottest part of the gas flame is known as the -
(A) Luminous zone (B) Dark zone (C) Blue zone (D) Yellow zone
63. During fractional distillation of the crude petroleum is heated to a temperature of about-
(A) 600°C (B) 400–500°C (C) 200°C (D) 100°C
64. Fractional distillation is based on the property that -
(A) Density of each fraction is different
(B) Molecular weight of each fraction is different
(C) Boiling point of each fraction is different
(D) Melting point of each fraction is different
65. Which fraction of petroleum has highest boiling point -
(A) Kerosene (B) Gasoline (C) Ether (D) Gas oil
66. Which of the following is used as fuel -
(A) Gasoline (B) Ether (C) Pitch tar (D) Grease
67. Coal is formed by the process of
(A) Carbonisation (B) Distillation (C) Vaporisation (D) Evaporation
68. Hydrocarbons contains -
(A) Carbon and hydrogen
(B) Carbon and oxygen
(C) Carbon and nitrogen (D) Carbon and carbon dioxide
69. Natural gas mainly contains -
(A) Propane (B) Butane (C) Methane (D) Ethane
70. Producer gas is not a good fuel because -
(A) It contains CO which is poisonous
(B) It contains CO2
(C) It contains CO2 which do not burn (D) It contains N2 which do not burn
71. Plants store solar energy in the form of -
(A) Electric energy (B) Thermal energy (C) Chemical energy (D) Bio energy
72. Bio gas is a mixture of -
(A) Methane + CO2 (B) Methane + CO (C) Ethane + CO2 (D) Ethane + CO
73. Water gas is a mixture of -
(A) H2 and N2 (B) H2 and CO2 (C) CO2 and N2 (D) CO and H2
74. Petroleum is -
(A) Lighter than water and soluble in it
(B) Heavier than water and insoluble in it
(C) Lighter than water and insoluble in it (D) Heavier than water and soluble in it