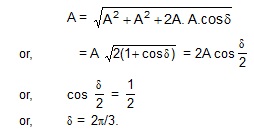Worked Out Examples
2. A block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Find the maximum force exerted by the spring on the block.
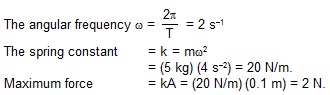
3. A particle executing simple harmonic motion has angular frequency 6.28 s–1 and ampitude 10 cm. Find (a) the time period, (b) the maximum speed, (c) the maximum acceleration, (d) the speed when the displacement is 6 cm from the mean position, (e) the speed at t = 1/6 s assuming that the motion starts from rest at t = 0.
4. A particle executes a simple harmonic motion of time period T. Find the time taken by the particle to go directly from its mean position to half the amplitude.
5. A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
Sol. Suppose the length of the spring is stretched by a length . The tension in the spring is k and this is the force by the spring on the block. The other force on the block is mg due to gravity. For equilibrium, mg = k or = mg/k. Take this position of the block as x = 0. If the block is further displaced by x, the resultant
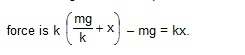
Thus, the resultant force is proportional to the displacement. The motion is simple harmonic with a time
We see that in vertical oscillations, gravity has no effect on time period. The only effect it has is to shift the equilibrium position by a distance mg/k as if the natural length is increased (or decreased if the lower end of the spring is fixed) by mg/k.
6. A particle suspended from a vertical spring oscillates 10 times per second. At the highest point of oscillation the spring becomes unstretched. (a) Find the maximum speed of the block. (b) Find the speed when the spring is stretched by 0.20 cm. Take g = p2 m/s2.
Sol.(a) The mean position of the particle during vertical oscillations is mg/k distance away from its position when the spring is unstretched. at the highest point, i.e., at an extreme position, the spring is unstretched.
Hence the amplitude is
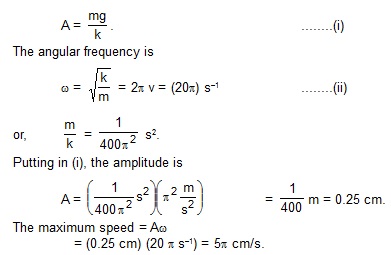
(b) When the spring is stretched by 0.20 cm, the block is 0.25 cm – 0.20 cm = 0.05 cm above the mean position. The speed at this position will be
7. The pulley shown in figure has a moment of inertia I about its axis and mass m. Find the time period of vertical oscillation of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.
Sol. Let us first find the equilibrium position. For rotational equilibrium of the pulley, the tensions in the two strings should be equal. Only then the torque on the pulley will be zero. Let this tension be T. The extension of the spring will be y = T/k, as the tension in the spring will be the same as the tension in the string. For translational equilibrium of the pulley,
the spring is extended by a distance mg/2k when the pulley is in equilibrium.
Now suppose, the centre of the pulley goes down further by a distance x. The total increase in the length of the string plus the spring 2x (x on the left of the pulley and x on the right). As the string has a constant length, the extension of the spring is 2x. The energy of the system is
8. The friction coefficient between the two blocks shown in figure is µ and the horizontal plane is smooth. (a) If the system is slightly displaced and released, find the time period. (b) Find the magnitude of the frictional force between the blocks when the displacement from the meanposition is x. (c) What can be the maximum amplitude if the upper block does not slip relative to the lower block ?
Sol. (a) For small amplitude, the two blocks oscillate together. The angular frequency is
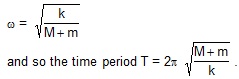
(b) The acceleration of the blocks at displacement x from the mean position is
The resultant force on the upper block is, therefore,
This force is provided by the friction of the lower block. Hence, the magnitude of the frictional force is
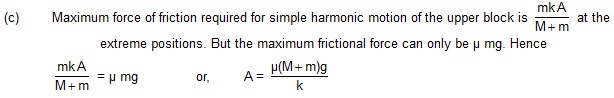
9. The left block in figure collides inelastically with the right block and sticks to it. Find the amplitude of the resulting simple harmonic motion.
Sol. Assuming the collision to last for a small interval only, we can apply the principle of conservation of momentum.
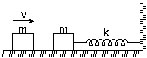
10. Describe the motion of the mass m shown in figure. The walls and the block are elastic.
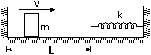
Sol. The block reaches the spring with a speed v. It now compresses the spring. The block is decelerated due to the spring force, comes to rest when 1/2 mv2 =1/2 kx2 and return back. It is accelerated due to the spring force till the spring acquires its natural length. The contact of the block with the spring is now broken. At this instant it has regained its speed v (towards left) as the spring is unstretched and no potential energy is sotred. This process takes half the period of oscillation i.e
. The block strikes the left wall after a time L/v and as the collision is elastic, it rebounds with the same speed v. After a time L/v, it again reaches the spring and the process is repeated. The block thus undergoes periodic motion with time period p
11. A block of mass m is suspended from the ceiling of a stationary elevator through a spring of spring constant k. Suddenly, the cable breaks and the elevator starts falling freely. Show that block now executes a simple harmonic motion of amplitude mg/k in the elevator.
Sol. When the elevator is stationary, the spring is stretched to support the block. If the extension is x, the tension is kx which should balance the weight of the block.
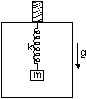
Thus, x = mg/k. As the cable breaks, the elevator starts falling with acceleration ‘g’. We shall work in he frame of reference of the elevator. Then we have to use a psuedo force mg upward on the block. This force will ‘balance’ the weight. Thus, the block is subjected to a net force kx by the spring when it is at a distance x from the position of unstretched spring. Hence, its motion in the elevator is simple harmonic with its mean position corresponding to the unstretched spring. Initially, the spring is stretched by x = mg/k, where the velocity of the block (with respect to the elevator) is zero. Thus, the amplitude of the resulting simple harmonic motion is mg/k.
12. The spring shown in figure is kept in a stretched position with extension x0 when the system is released. Assuming the horizontal surface to be frictionless, find the frequency of oscillation.
Sol. Considering “the two blocks plus the spring” as a system there is no external resultant force on the system. Hence the centre of mass of the system will remain at rest. The mean positions of the two simple harmonic motions occur when the spring becomes unstretched. If the mass m moves towards right through a distance x and the mass M moves towards left through a distance X before the spring acquires natural length,
x + X = x0. .............(i)
x and X will be the amplitudes of the two blocks m and M respectively. As the centre of mass should not change during the motion, we should also have
13. Assume that a narrow tunnel is dug between two diametrically opposite points of the earth. Treat the earth as a solid sphere of uniform density. Show that if a particle is released in this tunnel, it will execute a simple harmonic motion. Calculate the time period of this motion.
Sol.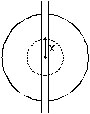 
Consider the situation shown in figure. Suppose at an instant t the particle in the tunnel is at a distance x from the centre of the earth. Let us draw a sphere of radius x with its centre at the centre of the earth. Only the part of the earth within this sphere will exert a net attraction on the particle. Mass of this part is
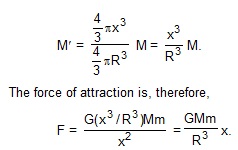
This force acts towards the centre of the earth. Thus, the resultant force on the particle is opposite to the displacement from the centre of the earth and is proportional to it. The particle, therefore, executes a simple harmonic motion in the tunnel with the centre of the earth as the mean position.
14. A simple pendulum of length 40 cm oscillates with an angular amplitude of 0.04 rad. Find (a) the time period, (b) the linear amplitude of the bob, (c) the speed of the bob when the string makes 0.02 rad with the vertical and (d) the angular acceleration when the bob is in momentary rest. Take g = 10 m/s2.
Sol.(a) The angular frequency is
15. A simple pendulum having a bob of mass m undergoes small oscillations with amplitude q0. Find the tension in the string as a function of the angle made by the string with the vertical. When is this tension maximum, and when is it minimum ?
Sol. Suppose the speed of the bob at angle q is v. Using conservation of energy between the extreme position and the position with angle q,
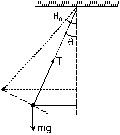
16. A simple pendulum is taken at a place where it separation from the earth’s surface is equal to the radius of the earth. Calculate the time period of small oscillations if the length of the string is 1.0m. Take g = p2 m/s2 at the surface of the earth.
Sol. At a height R (radius of the earth) the acceleration due to gravity is
17. A simple pendulum is suspended from the ceiling of a car accelerating uniformly on a horizontal road. If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
Sol. We shall work in the car frame. As it is accelerated with respect to the road, we shall have to apply a psuedo force ma0 on the bob of mass m.
For mean position, the acceleration of the bob with respect to the car should be zero. If q be the angle made by the string with the vertical, the tension, weight and the psuedo force will add to zero in this position.
Suppose, at some instant during oscillation, the string is further deflected by an angle a so that the displacement of the bob is x. Taking the components perpendicular to the string,
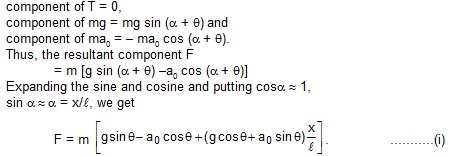
At x = 0, the force F on the bob should be zero, as this is the mean position. Thus by (i),
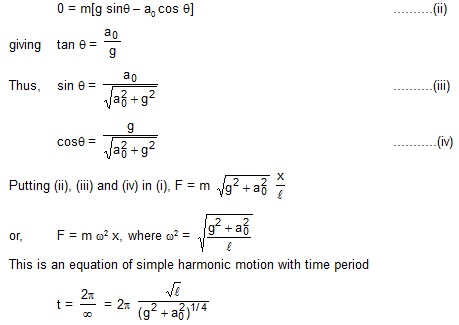
An easy working rule may be found out as follows. In the mean position, the tension, the weight and the psuedo force balance.
From figure, the tension is
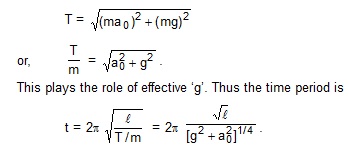
18. A uniform meter stick is suspended through a small pin hole at the 10 cm mark. Find the time peiod of small oscillation about the point of suspension.
Sol. Let the mass of the stick be m. The moment of inertia of the stick about the axis of rotation through the point of suspension is
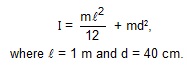
The separation between the centre of mass of the stick and the point of suspension is d = 40 cm. The time period of this physical pendulum is
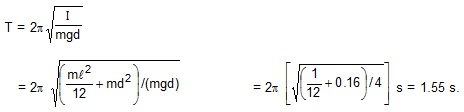
19. The moment of inertia of the disc used in a torsional pendulum about the suspension wire is 0.2 km-m2. If oscillates with a period of 2s. Another disc is placed over the first one and the time period of the system becomes 2.5 s. Find the moment of inertia of the second disc about the wire.
Sol. Let the torsional constant of the wire be k. The moment of inertia of the first disc about the wire is 0.2 kg-m2. Hence the time period is
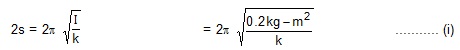
When the second disc having moment of inertia I1 about the wire is added, the time period is
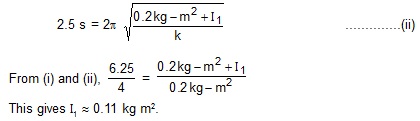
20. A uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time period of the system makes (a) small oscillations in the vertical plane about the suspension point and (b) angular oscillations in the horizontal plane about the centre of the rod.
Sol.(a) The oscillations take place about horizontal line through the point of suspension and perpendicular to the plane of the figure. The moment of inertia of the rod about this line is
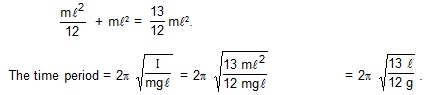
(b) The angular oscillations take place about the suspension wire. The moment of inertia about this line is ml2/12. The time period is
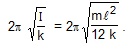
21. A particle is subjected to two simple harmonic motions
(b) The resultant of the two motions is a simple harmonic motion of the same angular frequency w. The amplitude of the resultant motion is
22. A particle is subjected to two simple harmonic motions in the same direction having equal amplitudes and equal frequency. If the resultant amplitude is equal to the amplitude of the individual motions, find the phase difference between the individual motions.
,d d.k nks ljy vkorZ xfr;ksa ftuds vk;ke o vko`fÙk leku gS ds vUrxZr xfreku gSA ;fn ifj.kkeh vk;ke vyx&vyx xfr;ksa ds vk;ke ds cjkcj gS rks vyx&vyx xfr;ksa ds chp dykUrj Kkr djksA
Sol. Let the amplitudes of the individual motions be A each. The resultant amplitude is also A. If the phase difference between the two motions is d,
