1. A spring of spring constant 50 N/m is compressed from its natural position through 1 cm. Find the work done by the spring-force on the agency compressing the spring.
Sol. The magnitude of the work is
1/2(kx2) = 1/2× (50 N/m) × (1 cm)2
= (25 N/m) × (1 × 10–2m )2 = 2.5 × 10–3 J
As the compressed spring will push the agency, the force will be opposite to the displacement of the point of application and the work will be negative. Thus, the work done by the spring-force is
–2.5 mJ.
2. A particle of mass 20 g is thrown vertically upwards with a speed of 10 m/s. Find the work done by the force of gravity during the time the particle goes up.
Sol. Suppose the particle reaches a maximum height h. As the velocity at the highest point is zero, we have
0 = u2 – 2gh
or, h = u2/2g
The work done by the foce of gravity is
–mgh = –mg(u2/2g) = –1/2(mu2)
= –(0.02 kg) × (10 m/s)2 = –1.0 J
3. Two charged particles A and B repel each other by a force k/r2,where k is a constant and r is the separation between them. The particle A is clamped to a fixed point in the lab and the particle B which has a mass m, is released from rest with an intial separation r0 from A. Find the change in the potential energy of two-particle system as the separation increases to a large value. What will be the speed of the particle B in this situation?
Sol. The situation is shown in figure (8.9). Take A + B as the system. The only external force acting on the system is that needed to hold A fixed.(You can imagine the experiment being conducted in a gravity free region or the particle may be kept and allowed to move on a smooth horizontal surface, so that the normal force balances the force of gravity). This force does no work on the system because it acts on the charge A which does not move. Thus , the external forces do no work and internal forces; are conservative, the total mechanical energy must, therefore, remain constant . there are two internal forces ; FAB acting on A and FBA acting on B. The force FAB does no work because it acts on A which does not move. The work done by FBA as the particle B is taken away is ,

4. A block of mass m slides along a frictionless surface as shown in the figure (8.10). If it is released from rest at A , what is its speed at B?

Sol. Take the block + the earth as the system. Only the block moves , so only the work done on the block will contribute to the gravitional potential energy. As it descends through a height h between A and B, the potential energy decreases by mgh. The normal contact force on the block by the surface does no work as it is perpendicular to its velocity. No external force does any work on the system. Hence,
increase in kinetic energy = decrease in potential energy
![]()
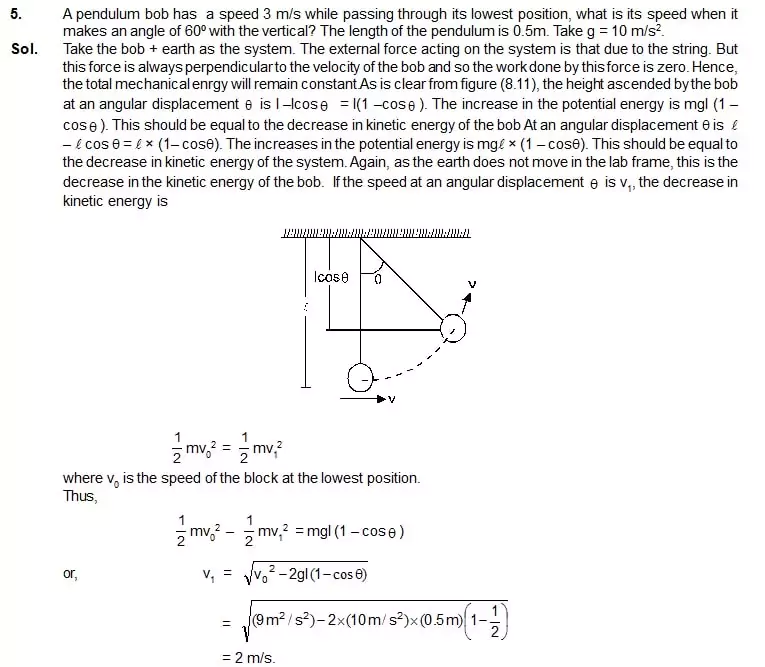
6. A block of mass m , attached to a spring constant k, oscillates on a smooth horizontable table . The other end of the spring is fixed to a wall. If it has a speed v when the spring is at natural length, how far will it move on the table before coming to an instantaneous rest ?
Sol. Consider the block + the spring as the system. The external forces acting on the system are (a) the force of gravity, (b) the normal force by the table and (c) the force by the wall. None of these do any work on this system and hence the total mechanical enery is conserved. If the block moves a distace x before comming to rest, we have,

7. A block of mass m is suspended through a spring of spring constant k and is in equilibrium. A sharp blow gives the block an initial downward velocity v. How far below the equilibrium position, the block comes to an instantaneous rest ?
Sol. Let us consider the block + the spring + the earth as the system. The system has gravitational potential energy corresponding to the force between the block and the earth as well as the elastic potential energy corresponding to the spring force. The total mechanical energy includes kinetic energy, gravitational potential energy and elastic potential energy.

Compare this with the result obtained in example. If we neglect gravity and consider the length of the spring in equilibrium position as the natural length, the answer is same. This simplification is often used while dealing with vertical springs.
1. When you lift a box from the floor and put it on an almirah the potential energy of the box increases, but there is no change in its kinetic energy. Is it a violation of conservation of energy ?
2. A particle is released from the top of an incline of height h. Does the kinetic energy of the particle at the bottom of the incline depend on the angle of incline? Do you need any more information to answer this question in Yes or No ?
3. Can the work by kinetic friction on an object be positive? zero ?
4. Can static friction dq nonzero work on an object ? If yes, give an example. If no, give reason.
5. Can normal force do a nonzero work on an object. If yes, give an example. If no, give reason.
6. Can kinetic energy of a system be increased without applying any external force on the system?
7. Is work - energy theorem valid in nonintertial frames ?
8. A heavy box is kept on a smooth inclined plane and is pushed up by a force F acting parallel to the plane. Does the work done by the force F as the box goes from A to B depend on how fast the box was moving at A and B? Does the work by the force of gravity depend on this ?
9. One person says that the potential energy of a particular book kept in an almirah is 20 J and the other says it is 30 J. Is one of them necessarily wrong ?
10. A book is lifted from the floor and is kept in an almirah. One person says that the potential energy of the book is increased by 20 J and the other says it is increased by 30 J. Is one of them necessarily wrong?
11. In one of the exercises to strengthen the wrist and fingers, a person squeezes and releases a soft rubber ball. Is the work done on the ball positive, negative or zero during compression ? During expansion ?
12. In tug of war, the team that exerts a larger tangential force on the ground wins. Consider the period in which a team is dragging the opposite team by applying a larger tangential force on the ground. List which of the following works are positve, which are negative and which are zero ?
(a) work by the winning team on the losing team.
(b) work by the losing team on the winning team
(c) work by the ground on the winning team
(d) work by the ground on the losing team
(e) total external work on the two teams.
13. When an apple falls from a tree what happens to its gravitational potential energy just as it reaches the ground ? After it strikes the ground ?
14. When you push you bicycle up on an incline the potential energy of the bicycle and yourself increases. Where does this energy come from ?
15. The magnetic froce on a charged particle is always perpendicular to its velocity. Can the magnetic force change the velocity of the particle? Speed of the particle?
16. A ball is given a speed v0 on a rough horizontal surface. The ball travels through a distance l on the surface and stops. (a) What are the initial and final kinetic energies of the ball (b) What is the work done by the kinetic friction?
17. Consider the situation of the previous question from a frame moving with a speed v0 parallel to the initial velocity of the block, (a) What are the initial and final kinetic energies ? (b) What is the work done by the kinetic friction ?
1. A heavy stone is thrown from a cliff of height h with a speed v. The stone will hit the ground with maximum speed if it is thrown
(A) vertically downward (B) vertically upward
(C) horizontally (D*) the speed does not depend on the initial direction.
2. Two springs A and B (kA = 2kB) are strettched by applying forces of equal magnitudes at the four ends. If the energy stored in A is E, that in B is -
(A) E/2 (B*) 2E (C) E (D) E/4
3. Two equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natrual length. The work done by the spring on each mass is -
(A) 1/2(kx2 ) (B) – 1/2(kx2) (C) 1/4(kx2 ) (D*) – 1/4(kx2)
4. The negative of the work done by the conservative internal forces on a system equals the change in
(A) total energy (B) kinetic energy (C*) potential energy (D) none of these
5. The work done by the external forces on a system equals the change in
(A*) total energy (B) kinetic energy (C) potential energy (D) none of these
6. The work done by all the forces (external and internal) on a system equals the change in
(A) total energy (B*) kinetic energy (C) potential energy (D) none of these
7. ______________ of a two particle system depends only on the separation between the two particles. The most appropriate choice for the blank space in the above sentence is
(A) kinetic energy (B) total mechanical energy
(C*) potential energy (D) total energy

9. A block of mass m slides down a smooth vertical circular track. During the motion, the block is in
(A) vertical equilibrium (B) horizontal equilibrium (C) radial equilibrium (D*) none of these
10. A particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is -

1. A heavy stone is thrown from a cliff of height h in a given direction. The speed with which it hits the ground
(A*) must depend on the speed of projection
(B*) must be larger than the speed of projection
(C) must be independent of the speed of projection
(D) may be smaller than the speed of projection
2. The total work done on a particle is equal to the change in its kinetic energy
(A*) always (B) only if the forces acting on it are conservative
(C) only if gravitational force alone acts on it (D) only if elastic force alone acts on it.
3. A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion of the particle takes place in a plane. If follows that
(A) its velocity is constant (B) its acceleration is constant
(C*) its kinetic energy is constant (D*) it moves in a circular path
4. Consider two observers moving with respect to each other at a speed v along a straight line.They observe a block of mass m moving a distance l on a rough surface. The following quantities will be same as observed by the two observers
(A) kinetic energy of the block at time t (B) work done by friction
(C) total work done on the block (D*) acceleration of the block.
5. You lift a suitcase from the floor and keep it on a table. The work done by you on the suitcase does not depen on -
(A*) the path taken by the suitcase (B*) the time taken by you in doing so
(C) the weight of the suitcase (D*) your weight.
6. No work is done by a force on an object if
(A*) the force is always perpendicular to its velocity
(B) the force is always perpendicular to its acceleration
(C*) the object is stationary but the point of application of the force moves on the object
(D*) the object moves in such a way that the point of application of the force remains fixed.
7. A particle of mass m is attached to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upward velocity v. The particle is just able to complete a circle
(A*) the string becomes slack when the particle reaches its highest point
(B) the velocity of the particle becomes zero at the highest point
(C) the kinetic energy of the ball in initial position was 1/2(mv2) = mgl.
(D*) the particle again passes through the initial position.
8. The kinetic energy of a particle continuously increases with time
(A) the resultant force on the particle must be parallel to the velocity at all instants.
(B*) the resultant force on the particle must be at an angle less than 90° with the velocity all the time
(C) its height above the ground level must continuously decrease
(D*) the magnitude of its linear momentum is increasing continuously
9. One end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement , the work done by the spring is 1/2(kx2). The possible cases are -
(A*) the spring was initially compressed by a distance x and was finally in its natural length
(B*) it was initially stretched by a distance x and finally was in its natural length
(C) it was initially in its natural length and finally in a compressed position
(D) it was initially in its natural length and finally in a stretched position
10. A block of mass M is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic energy of the block increases by 20 J in 1s.
(A) the tension in the string is Mg
(B*) the tension in the string is F
(C) the work done by the tension on the block is 20 J in the above 1 s.
(D) the work done by the force of gravity is – 20 J in the above 1s.
1. A porter lifts a suitcase weighing 20 kg from the platform and puts it on his head 2.0 m above the platform. Calculate the work done by the porter on the suitcase.
Sol. The kinetic energy of the suitcase was zero when it was at the platform and it again became zero when it was put on the head. The change in kinetic energy is zero and hence the total work done on the suitcase is zero. Two forces act on the suitcase, one due to gravity and the other due to the porter. Thus, the work done by the porter is negative of the work done by gravity. As the suitcase is lifted up, the work done by gravity is
W = – mgh
= – (20 kg) (9.8 m/s2) (2m) = – 392 J
The work done by the porter is 392 J = 390 J.
2. An elevator weighing 500 kg is to be lifted up at a constant velocity of 0.20 m/s. What would be the minimum horespower of the motor to be used ?
Sol. An the elevator is going up with a uniform velocity, the total work done on it is zero in any time interval. The work done by the motor is, therefore, equal to the work done by the force of gravity in that interval (in magnitude). The rate of doing work i.e., the power delivered is
P = F v = mgv
= (500 kg) (9.8 m/s2) (0.2 m/s) = 980 W.
Assuming no loss against friction etc. in the motor, the minimum horsepower of the motor is
P = 980 W =(980/746) hp = 1.3 hp.
3. A block of mass 2.0 kg is pulled up on a smooth incline of angle 30° with the horizontal. If the block moves with an acceleration of 1.0 m/s2, find the power delivered by the pulling force at a time 4.0s after the motion starts. What is the average power delivered during the 4.0 s after the motion
starts ?
Sol. The forces acting on the block are shown in figure. Resolving the forces parallel to the incline,
we get
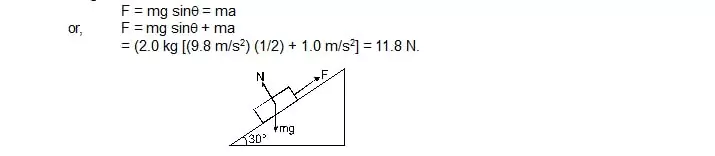
The velocity at t = 4.0 s is
v = at = (1.0 m/s2) (4.0 s) = 4.0 m/s.
The power delivered by the force at t = 4.0 s is
P = F.v = (11.8 N) (4.0 m/s) » 47 W.
The displacement during the first four seconds is
x = at2 = (1.0 m/s2) (16 s2) = 8.0 m.
The work done in these four seconds is, therefore,
W =F.d . = (11.8 N) (8.0 m) = 94.4 J.
The average power delivered = 94.4J/4.0s
= 23.6 W » 24 W.
4. A force F = (10 + 0.50 x) acts on a particle in the x direction where F is in newton and x in meter. Find the work done by this force during a displacement from x = 0 to x = 2.0 m.
Sol. As the force is variable, we shall find the work done in a small displacement x to x + dx and then integrate it to find the total work. The work done in this small displacement is
dW = F.dx. = (10 + 0.5x) dx

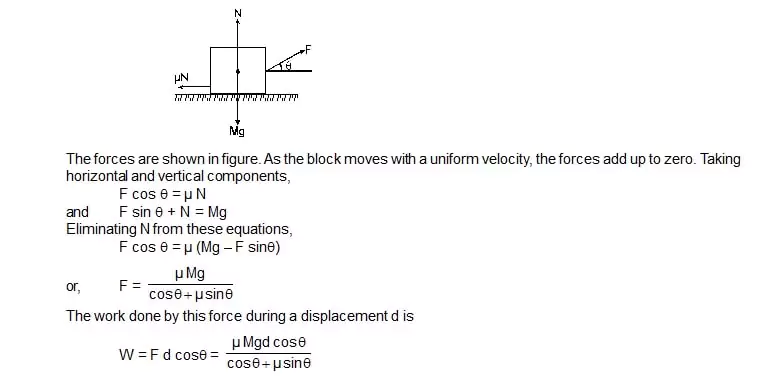
6. A block of mass M is pulled along a horizontal surface by applying a force at an angle q with the horizontal. The friction coefficient between the block and the surface is µ. If the block travels at a uniform velocity, find the work done by this applied force during a displacement d of the block.
Sol. Forces on the block are
(i) its weight Mg,
(ii) the normal force N,
(iii) the applied force F and
(iv) the kinetic friction µ N.
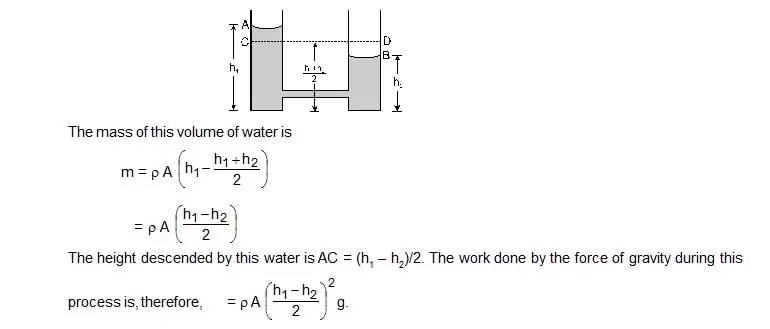
7. Two cylindrical vessels of equal cross-sectional area A contain water upto heights h1 and h2. The vessels are interconnected so that the levels in them become equal. Calculate the work done by the force of gravity during the process. The density of water is r.
Sol. Since the total volume of the water is constant, the height in each vessel after interconnection will be (h1 + h2)/2. The level in the left vessel shown in the figure, drops from A to C and that in the right vessel rises from B to D. Effectively, the water in the part AC has dropped down to DB.
8. What minimum horizontal speed should be given to the bob of a simple pendulum of length l so that is describes a complete circle ?
Sol. Suppose the bob is given a horizontal speed v0 at the bottom and it describes a complete vertical circle. Let its speed at the highest point be v. Taking the gravitational potential energy to be zero at the bottom, the conservation of energy gives,

9. A uniform chain of length l and mass m overhangs a smooth table with its two third part lying on the table. Find the kinetic energy of the chain as it completely slips off the table.

10. A block of mass m is pushed against a spring of spring constant k fixed at one end to a wall. The block can slide on a frictionless table as shown in figure. The natural length of the spring is L0 and it is compressed to half its natural length when the block is released. Find the velocity of the block as a function of its distance x from the wall.
.jpg)
11. A particle is placed at the point A of a frictionless track ABC as shown in figure. It is pushed slightly towards right. Find its speed when it reaches the point B. Take g = 10 m/s2.
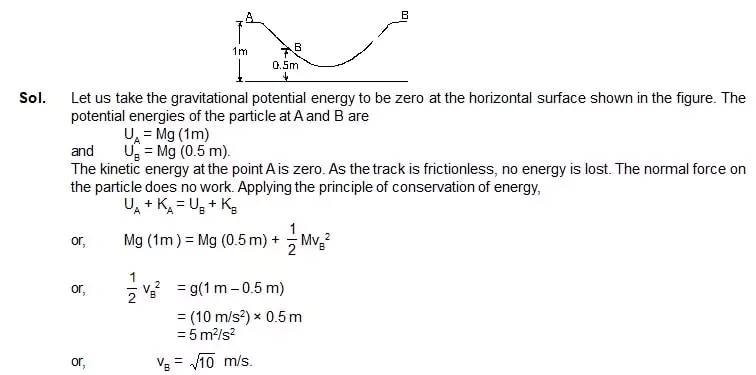
12. Figure shows a smooth curved truck terminating in a smooth horizontal part. A spring of spring constant 400 N/m is attached at one to a wedge fixed rigidly with the horizontal part. A 40 g mass is released from rest at a height of 4.9 m on the curved track. Find the maximum compression of the spring.


13. Figure shows a loop the loop track of radius R. A car (without engine) starts from a platform at a distance h above the top of the loop and goes around the loop without falling off the track. Find the minimum value of h for a successfull looping. Neglect friction.

Sol. Suppose the speed of the car at the topmost point of the loop is v. Taking the gravitational potential energy to be zero at the platform and assuming that the car starts with a negligible speed, the conservation of energy shows,
0 = – mgh + mv2
or, mv2 = 2 mgh ...........(1)
where m is the mass of the car. The car moving in a circle must have radial acceleration v2/R at this instant. The forces on the car are, mg due to gravity and N due to the contact with the track. Both these forces are in radial direction at the top of the loop. Thus, from Newton’s Law,
mg + N = mv2/R
or, mg + N = 2 mgh/R.
For h to be minimum, N should assume the minimum value which can be zero. Thus,
2 mg(hmin/R) = mg
or, hmin = R/2.
14. A heavy particle is suspended by a spring of length l. The particle is given a horizontal velocity v0. the string becomes slack at some angle and the particle proceeds on a parabola. Find the value of v0 if the particle passes through the point of suspension.
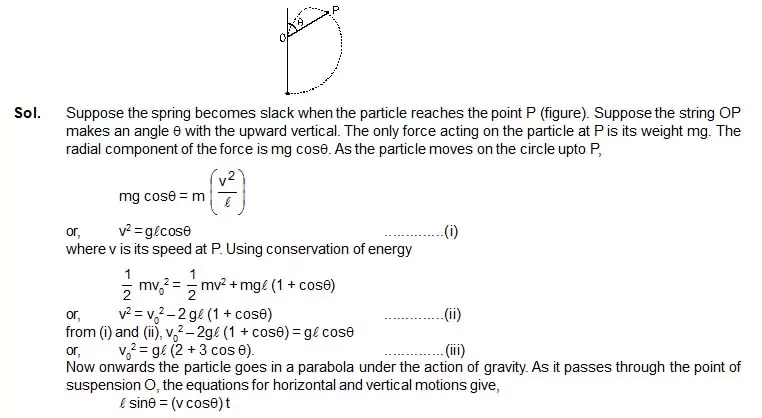
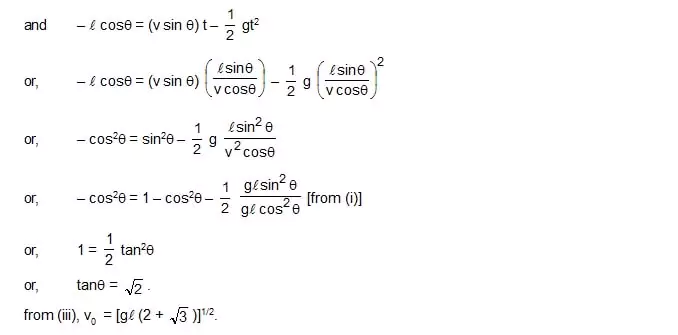
1. The mass of a cylist together with the bike is 90 kg. Calculate the increase in kinetic energy if the speed increases from 6.0 km/h to 12 km/h.
Ans. 375 J
2. A block of mass 2.00 kg moving at a speed of 10.0 m/s accelerates at 3.00 m/s2 for 5.00 s. Compute its final kinetic energy.
Ans. 625 J
3. A box is pushed through 4.0 m across a floor offering 100 N resistance. How much work is done by the resisting force?
Ans. 400 J
4. A block of mass 5.0 kg slides down an incline of inclination 30° and length 10 m. Find the work done by the force of gravity.
Ans. 245 J
5. A constant force of 2.50 N accelerates a stationary particle of mass 15 g through a displacement of 2.50 m. Find the work done and the avergae power delivered.
Ans. 6.25 J, 36.1 W

Ans. zero
7. A man moves on a straight horizontal road with a block of mass 2 kg in his hand. If he covers a distance of 40 m with an acceleration of 0.5 m/s2, find the work done by the man on the block during the motion.
Ans. 40 J
8. A force F = a + bx acts on a particle in the x direction where a and b are constants. Find the work done by this force during a displacement from x = 0 to x = d.
Ans. (a+0.5*bd) d
9. A block of mass 250 g slides down an incline of inclination 37° with a uniform speed. Find the work done against the friction as the block slides through 1.0 m.
Ans. 1.5 J
10. A block of mass m is kept over another block of mass M and the system rests on a horizontal surface (figure). A constant horizontal force F acting on the lower block produces an acceleration F/2(m+M) in the system, the two blocks always move together. (a) Find the coefficient of kinetic friction between the bigger block and the horizontal surface. (b) Find the frictional force acting on the smaller block. (c) Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.

11. A box weighing 2000 N is to be slowly slide through 20 m on a straight track having friction coefficient 0.2 with the box. (a) Find the work done by the person pulling the box with a chain at an angle q with the horizontal.
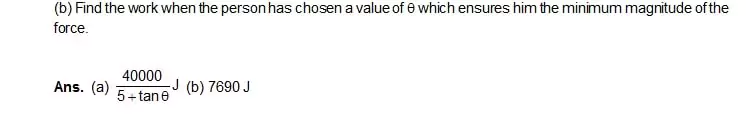
Ans. (a) (b) 7690 J
12. A block of weight 100 N is slowly slid up on a smooth incline of inclination 37° by a person. Calculate the work done by the person in moving the block through a distance of 2.0 m, if the driving force is (a) parallel to the incline and (b) in the horizontal direction.
Ans. (a) 120 J (b) 120J
13. Find the average frictional force needed to stop a car weighting 500 kg in a distance of 25 m if the initial speed is 72 km/h.
Ans. 4000 N
14. Find the average force needed to accelerated a car weighing 500 kg from rest to 72 km/h in a distance of 25m.
Ans. 4000 N

Ans. ma2d/2
16. A block of mass 2.0 kg kept at rest on an inclined plane of inclination 37° is pulled up the plane by applying a constant force of 20 N parallel to the incline. The force acts for one second. (a) Show that the work done by the applied force does not exceed 40 J. (b) Find the work done by the force of gravity in that one second if the work done by the applied force is 40 J. (c) Find the kinetic energy of the block at the instant the force ceases to act. Take g = 10 m/s2.
Ans. (b) – 24J (c) 16 J
17. A block of mass 2.0 kg is pushed down an inclined plane of inclination 37° with a force of 20 N acting parallel to the incline. It is found that the block moves on the incline with an acceleration of 10 m/s2. If the block started from rest, find the work done (a) by the applied force in the first second, (b) by the weight of the block in the first second and (c) by the frictional force acting on the block in the first second. Take g = 10 m/s2.
Ans. (a) 100 J (b) 60 J (c) – 60 J
18. A 250 g block slides on a rough horizontal table. Find the work done by the frictional force in bringing the block to rest if it is initially moving at a speed of 40 cm/s. If the friction coefficient between the table and the block is 0.1, how far does the block move before coming to rest?
Ans. – 0.02 J, 8.2 cm
19. Water falling from a 50 m high fall is to be used for generating electric energy. If 1.8 × 105 kg of water falls per hour and half the gravitational potential energy can be converted into electric energy, how many 100 W lamps can be lit ?
Ans. 122
20. A person is painting his house walls. He stands on a ladder with a bucket containing paint in one hand and a brush in other. Suddnely the bucket slips from this hand and falls down on the floor. If the bucket with the paint hand a masss of 6.0 kg and was at a height of 2.0 m at the time it slipped, how much gravitational potential energy is lost together with the paint ?
Ans. 118 J
21. A projectile is fired from the top of a 40 m height cliff with an initial speed of 50 m/s at an unknown angle. Find its speed when it hits the ground.
Ans. 58 m/s
22. The 200 m free style women’s swimming gold medal at Seol Olympic 1988 went to Heike Friendrich of East Germany when she set a new Olympic record of 1 minute and 57.56 seconds. Assume that she overed most of the distance with a uniform speed and had to exert 460 W to maintain her speed. Calculate the average force of resistance offered by the water during the swim.
Ans. 270 N
23. The US athlete Florence Griffith-Joyner won the 100 m sprint gold medal at Seol Olympic 1988 setting a new Olympic record of 10.54 s. Assume that she achieved her maximum speed in a very short time and then ran the race with that speed till she crossed the line. Take her mass to be
50 kg. (a) Calculate the kinetic energy of Griffith-Joyner at her full speed. (b) Assuming that the track, the wind etc. offered an average resistance of one tenth of her weight, calculate the work done by the resistance during the run. (c) What power Griffith-Joyner had to exert to maintain uniform speed ?
Ans. (a) 2250 J (b) – 4900 J (c) 465 W
24. A water pump lifts water from a level 10 m below the ground. Water is pumped at a rate of 30 kg/minute with negligible velocity. Calculate the minimum horsepower the engine should have to do this.
Ans. 6.6 × 10–2 hp
25. An unrully demonstrator lifs a stone of mass 200 g from the ground and throws it at his opponent. At the time of projection, the stone is 150 cm above the ground and has a speed of 3.00 m/s. Calculate the work done by the demonstrator during the process. If it takes one second for the demonstrator to lift the stone and throw, what horsepower does he use?
Ans. 3.84 J, 5.14 × 10–3 hp
26. In a factory it is desired to lift 2000 kg of metal through a distance of 12 m in 1 minute. Find the minimum horsepower of the engine to be used.
Ans. 5.3 hp
27. A sector company gives the following specifications about its products.
Weight of the scooter - 95 kg
Maximum speed - 60 km/h
Maximum engine power - 3.5 hp
Pick up time to get the maximum speed - 5 s
Check the validity of these specifications.
Ans. Seems to be somewhat overclaimed.
28. A block of mass 30.0 kg is being brought down by a chain. If the block acquires a speed of
40.0 cm/s in dropping down 2.00 m, find the work done by the chain during the process.
Ans. – 586 J
29. The heavier block in an At wood machine has a mass twice that of the lighter one. The tension in the spring is 16.0 N when the system is set into motion. Find the decrease in the gravitational potential energy during the first second after the system is released from rest.
Ans. 19.6 J
30. The two blocks in an Atwood machine have masses 2.0 kg and 3.0 kg. Find the work done by graivty during the fourth second after the system is released from rest.
Ans. 67 J
31. Consider the situation shown in figure. The system is released from rest and the block of mass 1.0 kg is found to have a speed 0.3 m/s after it has descended through a distance of 1m. Find the coefficient of kinetic friction between the block and the table.

Ans. 0.12
32. A block of mass 100 g is moved with a speed of 5.0 m/s at the highest point in a closed circular tube of radius 10 cm kept in a vertical plane. The cross-section of the tube is such that the block just fits in it. The block makes several oscillations inside the tube and finally stops at the lowest point. Find the work done by the tube on the block during the process.
Ans. – 1.45 J
33. A car weighing 1400 kg is moving at a speed of 54 km/h up a hill when the motor stops. If it is just able to reach the distination which is at a ehight of 10 m above the point, calculate the work done against friction (negative of the work done by the friction).
Ans. 20300 J
34. A small block of mass 200 g is kept at the top of a frictionless incline which is 10 m long and 3.2m high. How much work was required (a) to lift the block from the ground and put it at the top, (b) to slide the block up the incline? What will be the speed of the block when it reaches the ground if (c) if it falls off the incline and drops vertically on the ground (d) it slides down the incline? Take g = 10 m/s2.
Ans. (a) 6.4 J (b) 6.4 J (c) 8.0 m/s (d) 8.0 m/s
35. In a children’s park, there is a slide which has a total length of 10 m and a height of 8.0 m (figure). A vertical ladder is provided to reach the top. a boy weighing 200 N climbs up the ladder to the top of the slide and slides down to the ground. The average friction offered by the slide is three tenth of his weight. Find (a) the work done by the ladder on the boy as he goes up, (b) the work done by the slide on the boy as he comes down. (c) Find the work done by forces inside the body of the boy.

Ans. (a) zero (b) – 600 J (c) 1600 J
36. Figure shows a particle sliding on a frictionless track which terminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground ?

Ans. At a horizontal distance of 1 m from the end of the track.
37. A block weighing 10 N travles down a smooth curved track AB joined to a rough horizontal surface (figure). The rough surface has a friction coefficient of 0.20 with the block. If the block starts slipping on the track from a point 1.0 m above the horizontal surface, how far will it move on the rough surface?

Ans. 5.0 m
38. A uniform chain of mass m and length l overhangs a table with its two third part on the table. Find the work to be done by a person to put the hanging part back on the table. HCV 1_Ch.8_38
Ans. mg/18
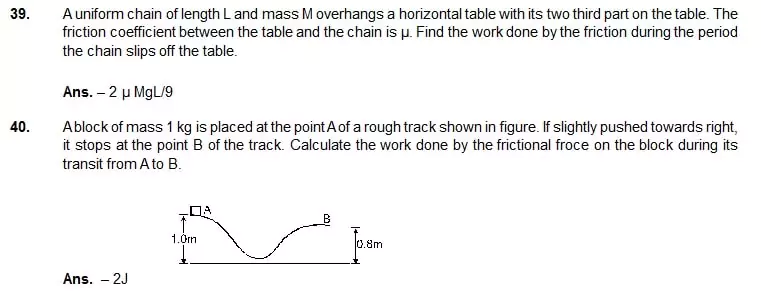
41. A block of mass 5.0 kg is suspended from the end of a vertical spring which is stretched by 10 cm under the load of the block. The block is given a sharp impulse from below so that it acquires an upward speed of 2.0 m/s. How high will it rise ? Take g = 10 m/s2.
Ans. 20 cm
42. A block of mass 250 g is kept on a vertical spring of spring constant 100 N/m fixed from below. The srping is now compressed to have a length 10 cm shorter than its natural length and the system is released from this position. How high does the block rise? Take g = 10 m/s2.
Ans. 20 cm
43. Figure shows a spring fixed at the bottom end of an incline of inclination 37°. A small block of mass 2 kg starts slipping down the incline from a point 4.8 m away from the spring. The block compresses the spring by 20 cm, stops momentarily and then rebounds through a distance of 1 m up the incline. Find (a) The friction coefficient between the plane and the block and (b) the spring constant of the spring. Take g = 10 m/s2.

Ans. (a) 0.5 (b) 1000 N/m
44. A block of mass m moving at a speed v compresses a spring through a distance x before its speed is halved. Find the spring constant of the spring.
Ans. 3mv2/4x2
45. Consider the situation shown in figure. Initially the spring is unstretched when the system is released from rest. Assuming no friction in the pulley, find the maximum elongation of the spring.

Ans. 2mg/k
46. A block of mass m is attached to two unstretched springs of spring constants k1 and k2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

47. A block of mass m sliding on a smooth horizontal surface with a velocity v meets a long horizontal spring fixed at one end and having spring constant k as shown in figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v when it comes back to the original position shown?

48. A small block of mass 100 g is pressed against a horizontal spring fixed at one end to compress the spring through 5.0 cm (figure). The spring constant is 100 N/m. When released, the block moves horizontally till it leaves the spring. Where will it hit the ground 2 m below the spring ?

Ans. At a horizontal distance of 1 m from the free end of the spring.
49. A small heavy block is attached to the lower end of a light rod of length l which can be rotated about its clamped upper end. What minimum horizontal velocity should the block be given so that it moves in a complete vertical circle ?
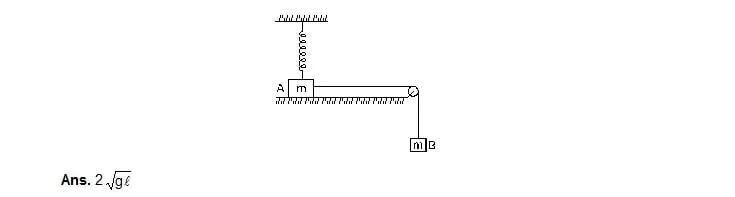
50. Figure shows two blocks A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to a spring of spring constant 40 N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g = 10 m/s2.
Ans. 1.5 m/s
51. One end of a spring of natural length h and spring constant k is fixed at the ground and the other is fitted with a smooth ring of mass m which is allowed to slide on a horizontal rod fixed at a height h (figure). Initially, the spring makes an angle of 37° with the vertical when the system is released from rest. Find the speed of the ring when the spring becomes vertical.

52. Figure shows a light rod of length l rigidly attached to a small heavy block at one end and a hook at the other end. The system is released from rest with the rod in a horizontal position. There is a fixed smooth ring at a depth h below the initial position of the hook and the hook gets into the ring as it reaches there. What should bethe minimum value of h so that the block moves in a complete circle about the ring ?
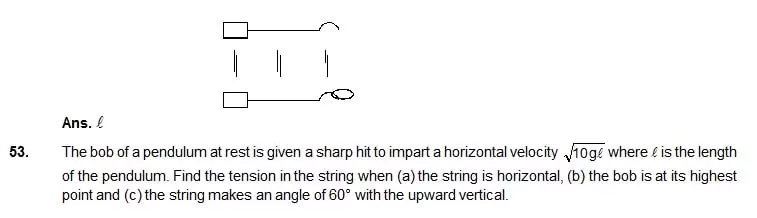
53. The bob of a pendulum at rest is given a sharp hit to impart a horizontal velocity where l is the length of the pendulum. Find the tension in the string when (a) the string is horizontal, (b) the bob is at its highest point and (c) the string makes an angle of 60° with the upward vertical.
Ans. (a) 8 mg (b) 5 mg (c) 6.5 mg
54. A simple pendulum consists of a 50 cm long string connected to a 100 g ball. The ball is pulled aside so that the string makes angle angle 37° with the vertical and is then released. Find the tension in the string when the bob is at its lowest position.
Ans. 1.4 N
55. Figure shows a smooth track, a part of which is a circle of radius R. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius or the track is horizontal.
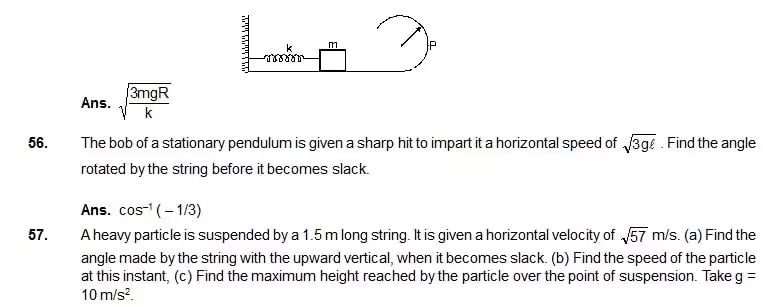
Ans. (a) 53° (b) 3.0 m/s (c) 1.2 m
58. A simple pendulum of length L having a bob of mass m is deflected from its rest position by an angle q and released (figure). The string hits a peg which is fixed at a distance x below the point of suspension and the bob starts going in a circle centred at the peg. (a) Assuming that initially the bob has a height less than the peg, show that the maximum height reached by the bob equals its initial height. (b) If the pendulum is released with q = 90° and x = L/2 find the maximum height reached by the bob above its lowest position before the string becomes slack. (c) Find the minimum value of x/L for which the bob goes in a complete circle about the peg when the pendulum is released from q = 90°.

Ans. (b) 5L/6 above the lowest point (c) 0.6
59. A particle slides on the surface of a fixed smooth sphere starting from the top most point. Find the angle rotated by the radius through the particle, when it leaves contact with the sphere.

62. Figure shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the inlcine from its bottom. (a) Find the minimum projection - speed v0 for which the particle reaches the top of the track. (b) Assuming that the projection - speed is 2v0 and that the block does not lose contact with the track before reaching its top, find the force acting on it when it reaches the top. (c) Assuming that the projection-speed is only slightly greater than v0, where will the block lose contact with the track ?
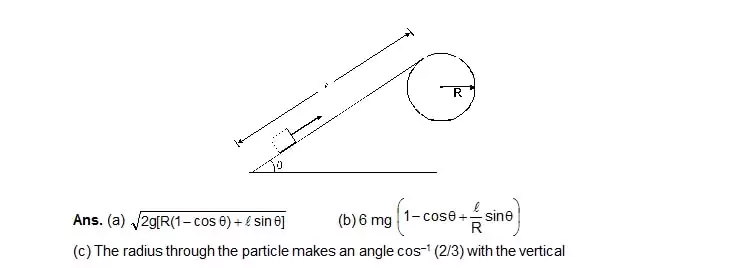
63. A chain of length l and mass m lies on the surface of a smooth sphere of radius R >l with one end tied to the top of the sphere. (a) Find the gravitational potential energy of the chain with reference level at the centre of the spehre. (b) Suppose the chain is rleased and slides down the sphere. Find the kinetic energy of the chain, when it has slid through an angle theta. (c) Find the tangential acceleration dv/dt of the chain when the chain starts sliding down.
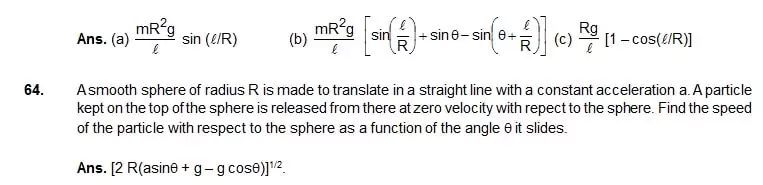
1. (D) 2. (B) 3. (D) 4. (C) 5. (A) 6. (B)
7. (C) 8. (C) 9. (D) 10. (C)
1. (A, B) 2. (A) 3. (C, D) 4. (D) 5. (A, B, D) 6. (A, C, D)
7. (A, D) 8. (B, D) 9. (A, B) 10. (B)
1. 375 J 2. 625 J 3. 400 J 4. 245 J 5. 6.25 J, 36.1 W
6. zero 7. 40 J 8. [a+(1/2)bd]d 9. 1.5 J
12. (a) 120 J (b) 120J 13. 4000 N 14. 4000 N 15. ma2d/2 16. (b) – 24J (c) 16 J
17. (a) 100 J (b) 60 J (c) – 60 J 18. – 0.02 J, 8.2 cm 19. 122
20. 118 J 21. 58 m/s 22. 270 N 23. (a) 2250 J (b) – 4900 J (c) 465 W
24. 6.6 × 10–2 hp 25. 3.84 J, 5.14 × 10–3 hp 26. 5.3 hp
27. Seems to be somewhat overclaimed. 28. – 586 J 29. 19.6 J 30. 67 J
31. 0.12 32. – 1.45 J 33. 20300 J
34. (a) 6.4 J (b) 6.4 J (c) 8.0 m/s (d) 8.0 m/s
35. (a) zero (b) – 600 J (c) 1600 J
36. At a horizontal distance of 1 m from the end of the track. 37. 5.0 m 38. mgl/18
