1. A wave is propagating on a long stretched string along its length taken as the positive x-axis. The wave equation is given as


2. Consider the wave y = (5 mm) sin (1 cm–1) x – (60 s–1) t]. Find (a) the amplitude (b) the wave number, (c) the wavelength, (d) the frequency, (e) the time period and (f) the wave velocity.
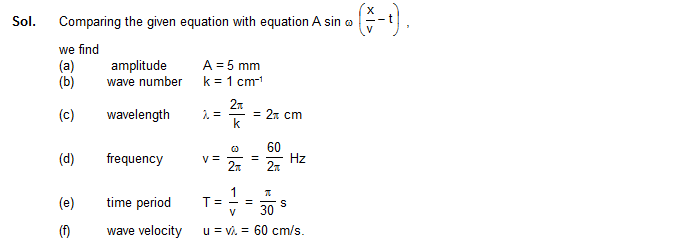
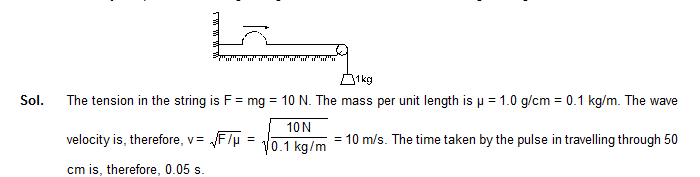
3. Figure shows a string of linear mass density 1.0 g/cm on which a wave pulse is travelling. Find the time taken by the pulse in travelling through a distance of 50 cm on the string. Take g = 10 m/s2.
4. The average power transmitted through a given point on a string supporting a sine wave is 0.20 W when the amplitude of the wave is 2.0 mm. What power will be transmiited through this point if the amplitude is increased to 3.0 mm.

5. Two waves are simultaneously passing through a string. The equations of the waves are given by

6. Two travelling waves of equal amplitudes and equal frequencies move in opposite direction along a string. They interfere to produce a standing wave having the equation.


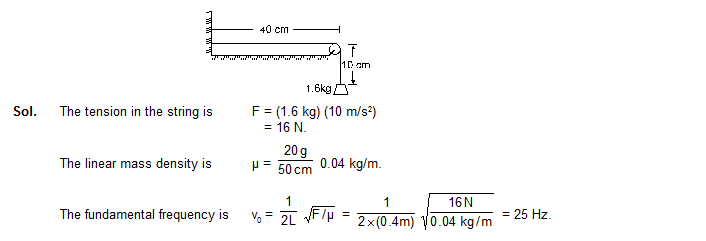
7. A 50 cm long wire of mass 20 g supports a mass of 1.6 kg as shown in figure. Find the fundamental frequency of the portion of the string between the wall and the pulley. Take g = 10 m/s2.
8. In a sonometer experiment, resonance is obtained when the experimental wire has a length of 21 cm between the bridges and the vibrations are excited by a tuning fork of frequency 256 Hz. If a tuning fork of frequency 384 Hz is used, what should be the length of the experimental wire to get the resonance ?

1. You are walking along a seashore and a mild wind is blowing. Is the motion of air a wave motion?
2. The radio and TV programmes, telecast at the studio, reach our antenna by wave motion. Is it a mechanical wave or nonmechanical?
3. A wave is represented by an equation y = c1 sin (c2x + c3t). In which direction is the wave going? Assume that c1, c2 and c3 are all positive.
4. Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than wavelength divided by 2pi.(pi=3.14)
5. Two wave pulse identical in shape but inverted with respect to each other are produced at the two ends of a stretched string. At an instant when the pulses reach the middle, the string becomes completely straight. What happens to the energy of the two pulses? [HCV_Chp 15_ Q.S.A_5]

7. What is the smallest positive phase constant which is equivalent to 7.5p?
8. A string clamped at both ends vibrates in its fundamental mode. Is there any position (except the ends) on the string which can be touched without disturbing the motion? What if the string vibrates in its first overtone ?
1. A sine wave is travelling in a medium. The minimum distance between the two particles, always having same speed, is
![]()
2. A sine wave is travelling in a medium. A particular particle has zero displacement at a certain instant. The particle closest to it having zero displacement is at a distance
![]()
3. Which of the following equations represents a wave travelling along Y-axis?
![]() .
.
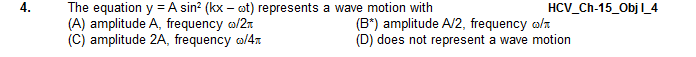
5. Which of the following is a mechanical wave ? HCV_Ch-15_Obj I_5
(A) radio waves (B) x-rays (C) light waves (D*) sound waves
6. A cork floating in a calm pond executes simple harmonic motion of frequency v when a wave generated by a boat passes by it. The frequency of the wave is HCV_Ch-15_Obj I_6
(A*) v (B) v/2 (C) 1/4 (D) 4
7. Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed vA and on B with speed vB. The ratio vA/vB is -
(A*) 1/2 (B) 2 (C) 1/4 (D) 4
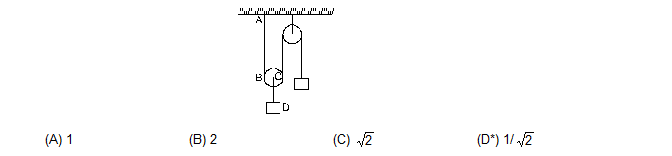
8. Both the strings, show in figure, are made of same material and have same cross-section. The pulleys are light. The wave speed of a transverse wave in the string AB is v1 and in CD it is v2. The v1/v2 is
(A) 1 (B) 2 (C) (D*) 1/
9. Velocity of sound in air is 332 m/s. Its velocity in vacuum will be HCV_Ch-15_Obj I_9

13. Consider two waves passing through the same string. Principle of superposition for displacement says that the net displacement of a particle on the string is sum of the displacements produced by the two waves individually. Suppose we state similar principles for the net velocity of the particle and the net kinetic energy of the particle. Such a principle will be valid for HCV_Ch-15_Obj I_13
(A) both the velocity and the kinetic energy (B*) the velocity but not for the kinetic energy
(C) the kinetic energy but not for the velocity (D) neither the velocity nor the kinetic energy
14. Two wave pulses travel in opposite directions on a string and approach each other. The shape of the one pulse in inverted with respect to the other. HCV_Ch-15_Obj I_14
(A) the pulses will collide with each other and vanish after collision
(B) the pulses will reflect from each other i.e., the pulse going towards right will finally move towards left and vice versa.
(C) the pulses will pass through each other but their shapes will be modified
(D*) the pulses will pass through each other without any change in their shape
15. Two periodic waves of amplitudes A1 and A2 pass through a region. If A1 > A2 , the difference in the maximum and minimum resultant amplitude possible is : HCV_Ch-15_Obj I_15
(A) 2A1 (B*) 2A2 (C) A1 + A2 (D) A1 – A2
16. Two waves of equal amplitude A, and equal frequency travels in the same direction in a medium. The amplitude of the resultant wave is HCV_Ch-15_Obj 1_16
(A) 0 (B) A (C) 2A (D*) between 0 and 2A.
17. Two sine waves travel in the same direction in a medium. The amplitude of each wave is A and the phase difference between the two waves is 120°. The resultant amplitude will be
![]()
18. The fundamental frequency of a string is proportional to
(A*) inverse of its length (B) the diameter (C) the tension (D) the density
19. A tuning fork of frequency 480 Hz is used to vibrate a sonometer wire having natural frequency 240 Hz. The wire will vibrate with a frequency of
(A) 240 Hz (B*) 480 Hz (C) 720 Hz (D) will not vibrate
20. A tuning fork of frequency 480 Hz is used to vibrate a sonometer wire having natural frequency
410 Hz. The wire will vibrate with a frequency
(A) 410 gV~Zt (B*) 480 gV~Zt (C) 820 gV~Zt (D) 960 gV~Zt
21. A sonometer wire of length l vibrate in fundamental mode when excited by a tuning fork of frequency 416 Hz. If the length is doubled keeping other things same, the string will
(A*) vibrate with a frequency of 416 Hz (B) vibrate with a frequency of 208 Hz
(C) vibrate with a frequency of 832 Hz (D) stop vibrating
22. A sonometer wire supports a 4 kg and load and vibrates in fundamental mode with a tuning fork of frequency 416 Hz. The length of the wire between the bridges is now doubled. In order to maintain fundamental mode, the load should be changed to -
(A) 1 kg (B) 2 kg (C) 8 kg (D*) 16 kg.
1. A mechanical wave propagates in a medium along the X-axis. The particles of the medium HCV_Ch-15_Obj II_1
(A) must move on the X-axis (B) must move on the Y-axis
(C*) may move on the X-axis (D*) may move on the Y-axis
2. A transverse wave travels along the Z-axis. The particles of the medium must move
(A) along the Z-axis (B) along the X-axis (C) along the Y-axis (D*) in the X-Y plane
3 Longitudinal waves cannot HCV_Ch-15_Obj II_3
(A) have a unique wavelength (B) transmit energy
(C) have a unique wave velocity (D*) be polarized
4. A wave going in a solid
(A) must be longitudinal (B*) may be longitudinal
(C) must be transverse (D*) may be transverse
5. A wave moving in a gas HCV_Ch-15_Obj II_5
(A*) must be longitudinal (B) may be longitudinal
(C) must be transverse (D) may be transverse
6. Two particles A and B have a phase difference of pi (pi=3.14) when a sine wave passes through the region
(A) A oscillates at half the frequency of B
(B*) A and B move in opposite directions
(C) A and B must be separated by half of the wavelength
(D*) the displacements at A and B have equal magnitudes
 .
.
9. Mark out the correct options.
(A) the energy of any small part of a string remains constant in a travelling wave
(B*) the energy of any small part of a string remains constant in a standing wave
(C) the energies of all the small parts of equal length are equal in a travelling wave
(D) the energies of all the small parts of equal length are equal in a standing wave.
10. In a stationary wave,
(A) all the particles of the medium vibrate in phase
(B) all the antinodes vibrate in phase
(C*) the alternate antinodes vibrate in phase
(D*) all the particles between consecutive nodes vibrate in phase
1. The displacement of a particle of a string carrying a travelling wave is given by
y = (3.0 cm) sin 6.28 (0.50x – 50t),
where x is in centimeter and t in second. Find (a) the amplitude, (b) the wavelength, (c) the frequency and (d) the speed of the wave.
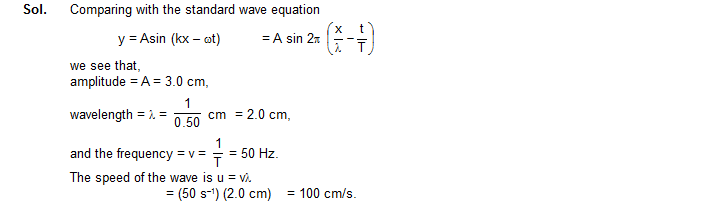

3. A long string having a cross-sectional area 0.80 mm2 and density 12.5 g/cm3, is subjected to a tension of 64 N along the X-axis. One end of this string is attached to a vibrator moving in transverse direction at a frequency of 20 Hz. At t = 0, the source is at a maximum displacement y = 1.0 cm. (a) Find the speed of the wave travelling on the string. (b) Write the equation for the wave. (c) What is the displacement of the particle of the string at x = 50 cm at time t = 0.05 s? (d) What is the velocity of this particle at this instant ?

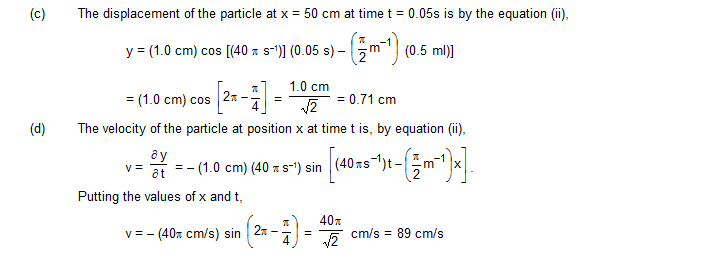
4. The speed of a transverse wave, going on a wire having a length 50 cm and mass 5.0 g, is 80 m/s. The area of cross-section of the wire is 1.0 mm2 and its Young’s modulus is 16 × 1011 N/m2. Find the extension of the wire over its natural length.
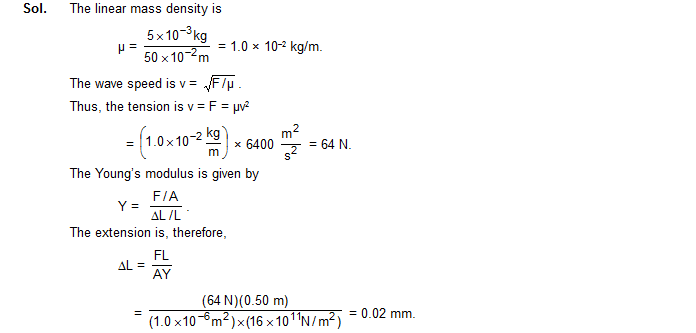
5. A uniform rope of length 12 m and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?

6. Two waves passing through a region are represented by
y = (1.0 m) sin [(3.14 cm–1) x – (157 s–1) t]
and y = (1.5 cm) sin [(1.57 cm–1)x – (314 s–1) t].
Find the displacement of the particle at x = 4.5 cm at time t = 5.0 ms.

7. The vibrations of a string fixed at both ends are described by the equation
y = (5.00 mm) sin [(1.57 cm–1) x] sin [(314 s–1)t].
(a) What is the maximum displacement of the particle at x = 5.66 cm? (b) What are the wavelengths and the wave speeds of the two transverse waves that combine to give the above vibration? (c) What is the velocity of the particle at x = 5.66 cm at time t = 2.00 s? (d) if the length of the string is 10.0 cm, locate the nodes and the antinodes. How many loops are formed in the vibration?



8. A guitar string is 90 cm long and has a fundamental frequency of 124 Hz. Where should it be pressed to produce a fundamental frequency of 186 Hz?
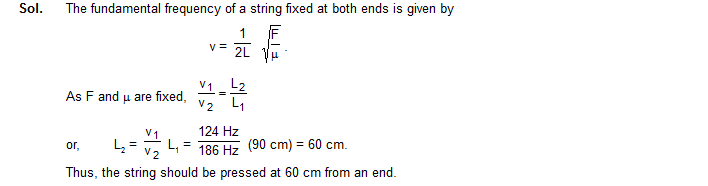
9. A sonometer wire has a total length of 1m between the fixed ends. Where should the two bridges be placed below the wire so that the three segments of the wire have their fundamental frequencies in the ration 1 : 2 : 3 ?
Sol. Suppose the lengths of the three segments are L1, L2 and L3 respectively. The fundamental frequencies are

10. A wire having a linear mass density 5.0 × 10–3 kg/m is stretched between two rigid supports with a tension of 450 N. The wire resonates at a frequency of 420 Hz. The next higher frequency at which the same wire resonates is 490 Hz. Find the length of the wire.
 EXERCISE
EXERCISE
1. A wave pulse passing on a string with a speed of 40 cm/s in the negative x-direction has its maximum at x = 0 at t = 0. Where will this maximum be located at t = 5 s ?
1. At x = – 2m

3. Figure shows a wave pulse at t = 0. The pulse moves to the right with a speed of 10 cm/s. Sketch the shape of the string at t = 1 s, 2 s and 3 s.

4. A pulse travelling on a string is represented by the function
![]()
where a = 5 mm and v = 20 cm/s. Sketch the shape of the string at t = 0, 1 s and 2s. Take x = 0 in the middle of the string.
5. The displacement of the particle at x = 0 of a stretched string carrying a wave in the positive
x-direction is given by f(t) = A sin (t/T). The wave speed is v. Write the wave equation.
![]() 6. A wave pulse is travelling on a string with a speed v towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = A sin (x/a), where A and a are constants.
6. A wave pulse is travelling on a string with a speed v towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = A sin (x/a), where A and a are constants.
(a) What are the dimensions of A and a? (b) Write the equation of the wave for a general time t, if the wave speed is v. [HCV_Ch-15_ExI_6]
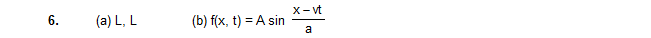
7. A wave propagates on a string in the positive x-direction at a velocity v. The shape of the string at t = t0 is given by g(x, t0) = A sin(x/a). Write the wave equation for a general time t.

8. The equation of a wave travelling on a string is
y = (0.10 mm) sin (31.4 m–1)x + 314 s–1)t ]
(a) In which direction does the wave travel?
(b) Find the wave speed, the wavelength and the frequency of the wave.
(c) What is the maximum displacement and the maximum speed of a portion of the string ?
8. (a) negative x-direction (b) 10 m/s, 20 cm, 50 Hz (c) 0.10 mm, 3.14 cm/s
9. A wave travels along the positive x-direction with a speed of 20 m/s. The amplitude of the wave is 0.20 cm and the wavelength 2.0 cm. (a) write a suitable wave equation which describes this wave. (b) What is the displacement and velocity of the particle at x = 2.0 cm at time t = 0 according to the wave equation written? Can you get different values of this quantity if the wave equation is written in a different fashion?
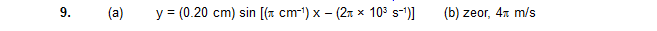
10. A wave is described by the equation
.
(a) Find the time period and the wavelength. (b) write the equation for the velocity of the particles. Find the speed of the particles at x = 1.0 cm at time t = 0.01 s. (c) what are the speeds of the particles at x = 3.0 cm, 5.0 cm and 7.0 cm at t = 0.01 s ? (d) What are the speeds of the particles at x = 1.0 cm at t = 0.011, 0.012, and 0.013 s?
10. (a) 20 ms, 4.0 cm (b) zero (c) zero (d) 9.7 cm/s, 18 cm/s, 25 cm/s
11. A particle on a stretched string supporting a travelling wave, takes 5.0 ms to move from its mean position to the extreme position. The distance between two consecutive particles, which are at their mean positions, is 2.0 cm. Find the frequency, the wavelength and the wave speed.
11. 50 Hz, 4.0 cm, 2.0 m/s
12. Figure shows a plot of the transverse displacements of the particles of a string at t = 0 through which a travelling wave is passing in the positive x-direction. The wave speed is 20 cm/s. Find (a) the amplitude,(b) the wavelength, (c) the wave number and (d) the frequency of the wave.

12. (a) 1.0 mm (b) 4 cm (c) 1.6 cm–1 (d) 5 Hz
13. A wave travelling on a string at a speed of 10 m/s causes each particle of the string to oscillate with a time period of 20 ms. (a) What is the wavelength of the wave ? (b) If the displacement of a particle is 1.5 mm at a certain instant, what will be the displacement of a particle 10 cm away from it at the same instant ?
13. (a) 20 cm (b) – 1.5 mm
14. A steel wire of length 64 cm weighs 5 g. If it is stretched by a force of 8 N, what would be the speed of a transverse wave passing on it?
64 lseh yEcs d.k ij LVhy ds rkj dk Hkkj 5 xzke gSA ;fn bldks 8 N cy ls rkuk tk;s] blls xqtjus okyh vuqizLFk rjax dh pky fdruh gksxh \
14. 32 m/s
15. A string of length 20 cm and linear mass density 0.40 g/cm is fixed at both ends and is kept under a tension of 16 N. A wave pulse in produce at t = 0 near an end as shown in figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).

16. A string of linear mass density 0.5 g/cm and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end (figure). The string can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20 cm/s. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period (c) What is the tension in the string ?

17. Two wires of different densities but same area of cross-section are soldered together at one end and are stretched to a tension T. The velocity of a transverse wave in the first wire is double of that in the second wire. Find the ratio of the density of the first wire to that of the second wire.
17. 0.25
18. A transverse wave described by
y = (0.02 m) sin [(1.0 m–1) x + (30 s–1) t]
propagates on a stretched string having a linear mass density of 1.2 × 10–4 kg/m. Find the tension in the string.
18. 0.108 N
19. A travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidally. The amplitude of vibration is 1.0 cm and the displacement becomes zero 200 times per second. The linear mass density of the string is 0.10 kg/m and it is kept under a tension of 90N. (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive x-direction and at t = 0, the end x = 0 is at its positive extreme position. Write the wave equation. (c) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10 ms.
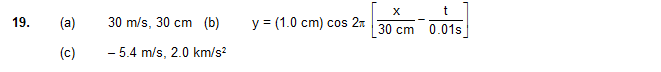
20. A string of length 40 cm and weighing 10 g is attached to a spring at one end and to a fixed wall at the other end. The spring has a spring constant of 160 N/m and is stretched by 1.0 cm. If a wave pulse is produced on the string near the wall, how much time will it take to reach the spring?
Ans. 0.05 s
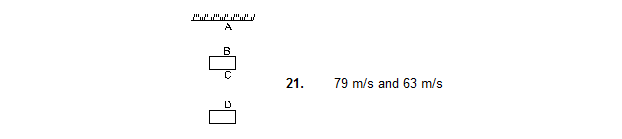
21. Two blocks each having a mass of 3.2 kg are connected by a wire CD and the system is suspended from the ceiling by another wire AB (figure). The linear mass density of the wire AB is 10 g/m and that of CD is 8 g/m. Find the speed of a transverse wave pulse produced in AB and in CD
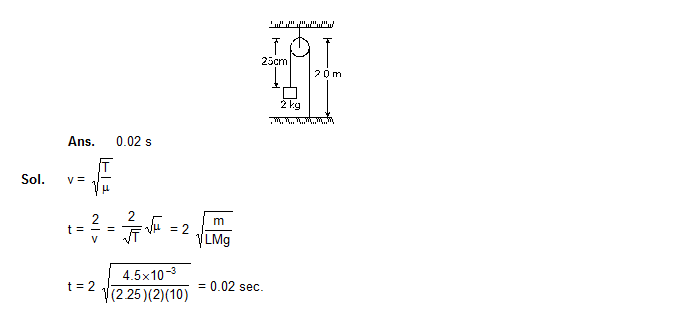
22. In the arrangement shown in figure, the string has mass of 4.5 g. How much time will it take for a transverse disturbance produced at the floor to reach the pulley ? Take g = 10 m/s2.
23. A 4.0 kg block is suspended from the ceiling of an elevator through a string having a linear mass density of 19.2 × 10–3 kg/m. Find the speed (with respect to the string) with which a wave pulse can proceed on the string if the elevator accelerates up at the rate of 2.0 m/s2. Take g = 10 m/s2.
23. 50 m/s
24. A heavy ball is suspended from the ceiling of a motor car through a light string. A transverse pulse travels at a speed of 60 cm/s on the string when the car is at rest and 62 cm/s when the car accelerates on a horizontal road. Find the acceleration of the car. Take g = 10 m/s2.
24. 3.7 m/s2
25. A circular loop of string rotates about its axis on a frictionless horizontal plane at a uniform rate so that the tangential speed of any particle of the string is v. If a small transverse disturbance is produced at a point of the loop, with what speed (relative to the string) will this disturbance travel on the string ?
25. v
26. A heavy but uniform rope of length L is suspended from a ceiling. (a) Write the velocity of a transverse wave travelling on the string as a function of the distance from the lower end. (b) If the rope is given a sudden sideways jerk at the bottom, how long will it take for the pulse to reach the ceiling? (c) A particle is dropped from the ceiling at the instant the bottom end is given the jerk. Where will the particle meet the pulse?
![]()
27. Two long strings A and B, each having linear mass density 1.2 × 10–2 kg/m, are stretched by different tensions 4.8 N and 7.5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A?
27. at t = 100 ms at x = 2.0 m
28. A transverse wave of amplitude 0.50 mm and frequency 100 Hz is produced on a wire stretched to a tension of 100 N. If the wave speed is 100 m/s, what average power is the source transmitting to the wire?
28. 49 mW
29. A 200 Hz wave with amplitude 1 mm travels on a long string of linear mass density 6 g/m kept under a tension of 60 N. (a) Find the average power transmitted across a given point on the string. (b) Find the total energy associated with the wave in a 2.0 m long portion of the string. [HCV_Ch-15_Ex_29]
29. (a) 0.47 W (b) 9.4 mJ
30. A tuning fork of frequency 440 Hz is attached to a long string of linear mass density 0.01 kg/m kept under a tension of 49 N. The fork produces transverse waves of amplitude 0.50 mm on the string. (a) Find the wave speed and the wavelength of the waves. (b) Find the maximum speed and acceleration of a particle of the string. (c) At what average rate is the tuning fork transmitting energy to the string?
30. (a) 70 m/s, 16 cm (b) 1.4 m/s, 3.8 km/s (c) 0.67 W
31. Two waves, travelling in the same direction through the same region, have equal frequencies, wavelengths and amplitudes. If the amplitude of each wave is 4 mm and the phase difference between the waves is 90°, what is the resultant amplitude?
![]()
32. Figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm/s. Sketch the shape of the string at t = 4 ms, 8 ms and 12 ms.
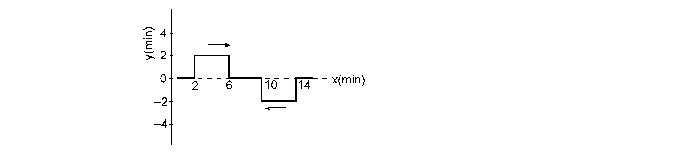
33. Two waves, each having a frequency of 100 Hz and a wavelength of 2.0 cm, are travelling in the same direction on a string. What is the phase difference between the waves (a) if the second wave was produced 0.015 s later than the first one at the same place, (b) if the two waves were produced a distance 4.0 cm behind the second one? (c) If each of the waves has an amplitude of 2.0 mm, what would be the amplitudes of the resultant waves in part (a) and (b) ?
![]()
34. If the speed of a transverse wave on a stretched string of length 1 m is 60 m/s, what is the fundamental frequency of vibration?
34. 30 Hz
35. A wire of length 2.00 m is stretched to a tension of 160 N. If the fundamental frequency of vibration is 100 Hz, find its linear mass density.
35. 1.00 g/m
36. A steel wire of mass 4.0 g and length 80 cm is fixed at the two ends. The tension in the wire is 50 N. Find the frequency and wavelength of the fourth harmonic of the fundamental.
36. 250 Hz, 40 cm
37. A piano wire weighing 6.00 g and having a length of 90.0 cm emits a fundamental frequency corresponding to the “Middle C” (v = 261.63 Hz). Find the tension in the wire.
37. 1480 N
38. A sonometer wire having a length of 1.50 m between the bridges vibrates in its second harmonic in resonance with a tuning fork of frequency 256 Hz. What is the speed of the transverse wave on the wire?
Ans. 384 m/s
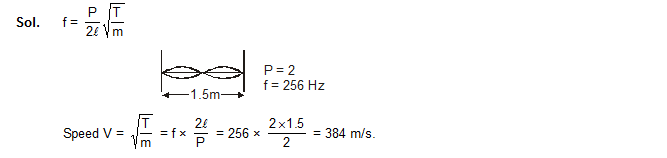
39. The length of the wire shown in figure between the pulleys is 1.5 m and its mass is 12.0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.

39. 70 Hz
40. A one metre long stretched string having a mass of 40 g is attached to a tuning fork. The fork vibrates at 128 Hz in a direction perpendicular to the string. What should be the tension in the string if it is to vibrate in four
loops?
40. 164 N
41. A wire, fixed at both ends is seen to vibrate at a resonant frequency of 240 Hz and also at 320 Hz. (a) what could be the maximum value of the fundamental frequency ? (b) If transverse waves can travel on this string at a speed of 40 m/s, what is its length ? [HCV_Ch-15_ExI_41]
41. (a) 80 Hz (b) 25 cm
42. A string, fixed at both ends, vibrates in a resonant mode with a separation of 2.0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1.6 cm. Find the length of the string. [HCV_Ch-15_ExI_42]
42. 8.0 cm
43. A 660 Hz tuning fork sets up vibration in a string clamped at both ends. The wave speed for a transverse wave on this string is 220 m/s and the string vibrates in three loops. (a) Find the length of the string. (b) If the maximum amplitude of a particle is 0.5 cm, write a suitable equation describing the motion.
44. A particular guitar wire is 30.0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
44. 26.7 cm, 23.8 cm, 22.4 cm and 20.0 cm
45. A steel wire fixed at both ends has a fundamental frequency of 200 Hz. A person can hear sound of maximum frequency 14 kHz. What is the highest harmonic that can be played on this string which is audible to the person?
45. 70
46. Three resonant frequencies of a string are 90, 150 and 210 Hz. (a) Find the highest possible fundamental frequency of vibration of this string. (b) Which harmonics of the fundamental are the given frequencies ? (c) Which overtone are these frequencies. (d) If the length of the string is 80 cm, what would be the speed of a transverse wave on this string ? [HCV_Ch-15_Ex_46]
46. (a) 30 Hz (b) 3rd, 5th and 7th (c)
47. Two wires are kept tight between the same pair of supports. The tensions in the wires are in the ratio 2 : 1, the radii are in the radio 3 : 1 and the densities are in the ratio 1 : 2. Find the ratio of their fundamental frequencies.
47. 2 : 3
48. A uniform horizontal rod of length 40 cm and mass 1.2 kg is supported by two identical wires as shown in figure. Where should a mass of 4.8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m/s2.

48. 5 cm from the left end
49. Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced in 40 N. The cross-sectional area of the steel wire is 1.0 mm2 and that of the aluminium wire is 3.0 mm2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node? The density of aluminium is 2.6 g/cm3 and that of steel is 7.8 g/cm3.

50. A string of length L fixed at both ends vibrates in its fundamental mode at a frequency v and a maximum amplitude A. (a) Find the wavelength and the ware number k. (b) Take the origin at one end of the string and X-axis along the string. Take the Y-axis along the direction of the displacement. Take t = 0 and the instant when the middle point of the string passes through its mean position and is going towards the positive y-direction. Write the equation describing the standing wave. [HCV_Ch-15_Ex_50]
51. A 2 m long string fixed at both ends is set into vibrations in its first overtone. The wave speed on the string is 200 m/s and the amplitude is 0.5 cm. (a) Find the wavelength and the frequency. (b) Write the equation giving the displacement of different points as a function of time. Choose the X-axis along the string with the origin at one end at t = 0 at the instant when the point x = 50 cm has reached its maximum displacement.
![]()

52. (a) 300 Hz (b) 0, 10 cm, 20 cm, 30 cm (c) 30 cm (D)20 cm, 60 m/s
54. A 40 cm wire having a mass of 3.2 g is stretched between two fixed supports 40.05 cm apart. In its fundamental mode, the wires vibrates at 220 Hz. If the area of cross-section of the wire is 1.0 mm2, find its Young’s modulus.
54. 1.98 × 1011 N/m2
55. Figure shows a string stretched by a block going over a pulley. The string vibrates in is length harmonic in unison with a particular tuning fork. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in is eleventh harmonic. Find the density of the material of the block.

56. A 2.00 m long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
56. (a) 10 hz, 30 Hz, 50 Hz (b) 8.00 m, 1.60 m
57. A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in figure. The thread goes over a fixed pulley and supports a weight to produce a tension. The lowest frequency with which the heavy string resonates is 120 Hz. If the movable support is pushed to the right by 10 cm so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate?
