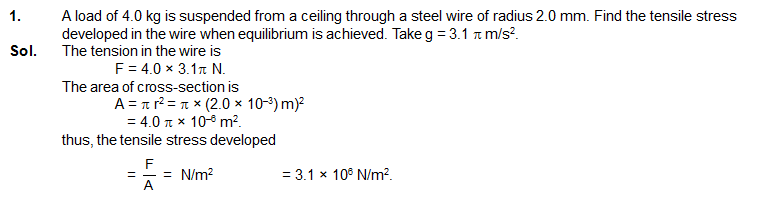

3. A steel wire of length 2.0 m is stretched through 2.0 mm. The cross-sectional area of the wire is 4.0 mm2. Calculate the elastic potential energy stored in the wire
in the stretched condition. Young’s modulus of steel = 2.0 × 1011 N/m2.

4. Water is kept in a beaker of radius 5.0 cm. Consider a diameter of the beaker on the surface of the water. Find the force by which the surface on one side of the
diameter pulls the surface on the other side. Surface tension of water = 0.075 N/m.
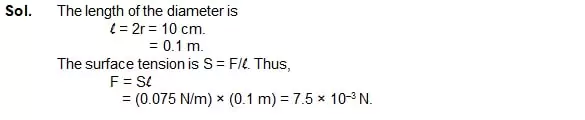
5. A water drop of radius 10–2 m is broken into 1000 equal droplets. Calculate the gain in surface energy. Surface tension of water is 0.075 N/m.
Sol. The volume of the original drop is

6. Find the excess pressure inside a mercury drop of radius 2.0 mm. The surface tension of mercury = 0.464 N/m.
Sol. The excess pressure inside the drop is
P2 = P1 = 2S/R

7. A 0.02 cm liquid column balances the excess pressure inside a soap bubble of radius 7.5 mm. Determine the density of the liquid. Surface tension of soap solution = 0.03 N/m.
Sol. The excess pressure inside a soap bubble is

8. A capillary tube of radius 0.20 mm is dipped vertically in water. Find the height of the water column raised in the tube. Surface tension of water = 0.075 N/m and density of water = 1000 kg/m3. Take g = 10 m/s2.
Sol. We have,
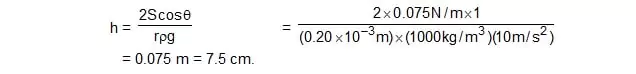
9. An air bubble of diameter 2 mm rises steadily through a solution of density 1750 kg/m3 at the rate of 0.35 cm/s. Calculate the coefficient of viscosity of the solution. The density of air is negligible.
Sol.The force of buoyancy B is equal to the weight of the displaced liquid. Thus,

1. The ratio stress/strain remains constant for small deformation of a metal wire. When the deformation is made larger, will this ratio increase or decrease?
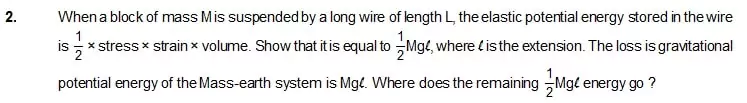
3. When the skeleton of an elephant and the skeleton of a mouse are prepared in the same size, the bones of the elephant are shown thicker than those of the mouse.
Explain why the bones of an elephant are thicker than proportionate. The bones are expected to withstand the stress due to the weight of the animal.
4. The yield point of a typical solid is about 1%. Suppose you are lying horizontally and two persons are pulling your hands and two person are pulling your legs
along your own length. How much will be the increase in your length if the strain is 1%? Do you think your yield point is 1% or, much less than that ?
5. When rubber sheets are used in a shock absorber, what happens to the energy of vibration?
6. If a compressed spring is dissolved in acid, what happens to the elastic potential energy of the spring ?
7. A steel blade placed gently on the surface of water floats on it. If the same blade is kept will inside the water, it sinks. Explain.
8. When some wax is rubbed on a cloth, it becomes waterproof. Explain.
9. The contact angle between pure water and pure silver is 90°. If a capillary tube made of silver is dipped at one end in pure water, will the water rise in the capillary ?
10. It is said that a liquid rises or is depressed in a capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface
tension of the liquid is zero ?
11. The contact angle between water and glass is 0°. When water is poured in a glass to the maximum of its capacity, the water surface is convex upward. The angle of
contact in such a situation is more than 90°. Explain.
12. A uniform vertical tube of circular cross-section contains a liquid. The contact angle is 90°. Consider a diameter of the tube lying in the surface of the liquid.
The surface to the right of this diameter pulls the surface on the left of it. What keeps the surface on the left in equilibrium?
13. When a glass capillary tube is dipped at one end in water, rises in the tube. The gravitational potential energy is thus increased. Is it a violation of conservation of energy ?
14. If a mosquito is dipped into water and released, it is not able to fly till it is dry again. Explain.
15. The force of surface tension acts tangentially to the surface whereas the force due to air pressure acts perpendicularly on the surface. How is then the force due to
excess pressure inside a bubble balanced by the force due to the surface tension ?
16. When the size of a soap bubble is increased by pushing more air in it, the surface area increases. Does it mean that the average separation between the surface molecules is increased ?
17. Frictional force between solids operates even when they do not move with respect to each other. Do we have viscous force acting between two layers even if there is no relative motion ?
18. Water near the bed of a deep river is quiet while that near the surface flows. Given reasons.
19. If water in one flask and castor oil in other are viotently shaken and kept on a table, which will come to rest earlier ?
1. A rope 1 cm in diameter breaks if the tension in it exceeds 500 N. The maximum tension that may be given to a similar rope of diameter 2 cm is
(A) 500 N (B) 250 N (C) 1000 N (D*) 2000 N.
2. The breaking stress of a wire depends on
(A*) material of the wire (B) length of the wire
(C) radius of the wire (D) shape of the cross-section.
3. A wire can sustain the weight of 20 kg before breaking. If the wire is cut into two equal parts, each part can sustain a weight of
(A) 10 kg (B*) 20 kg (C) 40 kg (D) 80 kg
4. Two wires A and B are made of same material. The wire A has a length L and diameter r while the wire B has an length 2L and diameter r/2. If the two wires are stretched by the same force, the elongation in A divided by the elongation in B is -
(A*) 1/8 (B) 1/4 (C) 4 (D) 8
5. A wire alongates by 1.0 mm when a load W is hanged from it. If this wire goes over a pulley and two weights W each are hung at the two ends, the elongation of the wire will be
(A) 0.5 m (B*) 1.0 mm (C) 2.0 mm (D) 4.0 mm
6. A heavy uniform rod is hanging vertically from a fixed support. It is stretched by its own weight. The diameter of the rod is
(A*) smallest at the top and gradually increases down the rod
(B) largest at the top and gradually decreases down the rod
(C) uniform everywhere
(D) maximum in the middle
9. A heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break
(A) when the mass is at the highest point
(B*) when the mass is at the lowest point
(C) when the wire is horizontal
(D) at an angle of cos–1 (1/3) from the upward vertical
10. When a metal wire elongates by hanging a load on it, the gravitational potential energy id decreased.
(A) this energy completely appears as the increased kinetic energy of the block
(B) this energy completely appears as the increased elastic potential energy of the wire
(C) this energy completely appears as heat
(D*) none of these
11. By a surface of a liquid we mean
(A) a geometrical plane like x = 0 (B) all molecules exposed to the atmosphere
(C*) a layer of thickness of the order of 10–8 m (D) a layer of thickness of the order of 10–4 m.
12. An ice cube is suspended in vacuum in a gravity free hall. As the ice melts it
(A) will retain its cubical shape (B*) will change its shape to spherical
(C) will fall down on the floor of the hall (D) will fly up
13. When water droplets merge to form a bigger drop
(A*) energy is liberated
(B) energy is absorbed
(C) energy is neither liberated nor absorbed
(D) energy may either be liberated or absorbed depending on the nature of the liquid
14. The dimension ML–1T–2 can correspond to
(A) moment of a force (B) surface tension
(C*) modulus of elasticity (D) coefficient of viscosity
15. Air is pushed into a soap bubble of radius r to double its radius. If the surface tension of the soap solution is S, the work done in the process is ![]()
16. If more air is pushed in a soap bubble, the pressure it
(A*) decreases (B) increases (C) remains same (D) becomes zero
17. If the soap bubbles of different radii are connected by a tube,
(A) air flows from bigger bubble to the smaller bubble till the size become equal
(B) air flows from bigger bubble to the smaller bubble till the sizes are interchanged
(C*) air flows from the smaller bubble to the bigger
(D) there is no flow of air.
18. Figure shows a capillary tube of radius r dipped into water. If the atmospheric pressure is P0, the pressure at point A is
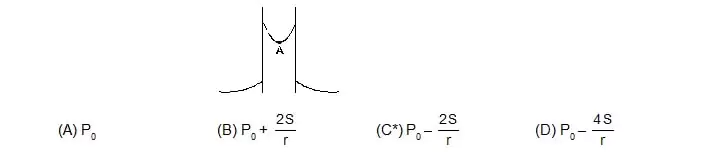
19. The excess pressure inside a soap bubble is twice the excess pressure inside a second soap bubble. The volume of the first bubble is n times the volume of the second where n is
(A) 4 (B) 2 (C) 1 (D*) 0.125
20. Which of the following graphs may represent the relation between the capillary rise h and the radius r of the capillary ?
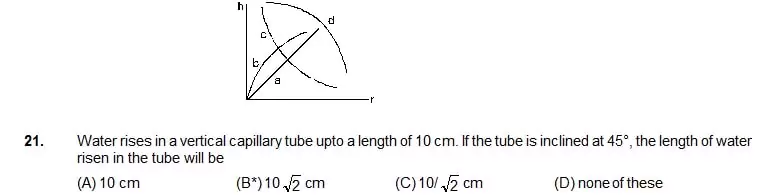
22. 20 cm long capillary tube is dipped in water. The water rises up to 8 cm. If the entire arrangement is put in a freely falling elevator, the length of water column in the capillary tube will be
(A) 8 cm (B) 6 cm (C) 10 cm (D*) 20 cm
23. Viscosity is a property of
(A) liquids only (B) solids only
(C) solids and liquids only (D*) liquids and gases only
24. The force of viscosity is
(A*) electromagnetic (B) gravitational (C) nuclear (D) weak
![]()
26. A raindrop falls near the surface of the earth with almost uniform velocity because HCV_Ch-14_Obj I_26
(A) its weight is negligible
(B) the force of surface tension balances its weight
(C*) the force of viscosity of air balances its weight
(D) the drops are charged and atmospheric electric field balances its weight
27. A piece of wood is taken deep inside a long column of water and released. It will move up
(A) with a constant upward acceleration (B*) with a decreasing upward acceleration
(C) with a deceleration (D) with a uniform velocity
28. A solid sphere falls with a terminal velocity of 20 m/s in air. If it is allowed to fall in vacuum,
(A) terminal velocity will be 20 m/s (B) terminal velocity will be less than 20 m/s
(C) terminal velocity will be more than 20 m/s (D*) there will be no terminal velocity.
29. A spherical ball is dropped in a long column of a viscous liquid. The speed of the ball as a function of time may be best represented by the graph
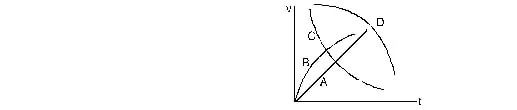
(A) A (B*) B (C) C (D) D
1. A student plots a graph from his readings on the determination of Young’s modulus of a metal wire but forgets to put the labels (figure). The quantities on X and Y axis may be respectively
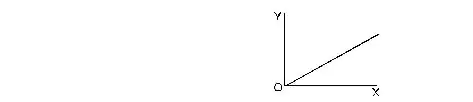
(A*) weight hung and length increased (B*) stress applied and length increased
(C*) stress applied and strain developed (D*) length increased and the weight hung
2. The properties of a surface are different from those of the bulk liquid because the surface molecules
(A) are smaller than other molecules
(B) acquire charge due to collision from air molecules
(C*) find different type of molecules in the their range of influence
(D*) feel a net force in one direction
3. The rise of a liquid in a capillary tube depends on
(A*) the material (B*) the length
(C) the outer radius (D*) the inner radius of the tube
4. The contact angle between a solid and a liquid is a property of
(A*) the material of the solid (B*) the material of the liquid
(C) the shape of the solid (D) the mass of the solid
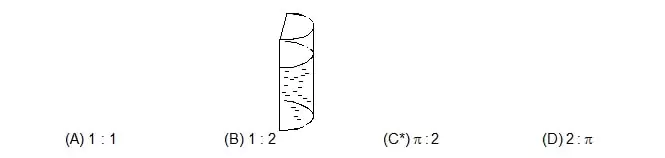
5. A liquid is contained in a vertical tube of semicircular cross-section (figure). The contact angle is zero. The force of surface tension on the curved part and one the flat part are in ratio
6. When a capillary tube is dipped into a liquid, the liquid neither rises nor falls in the capillary
(A) the surface tension of the liquid must be zero
(B) the contact angle must be 90°
(C*) the surface tension may be zero
(D*) the contact angle may be 90°.
7. A solid sphere moves at a terminal velocity of 20 m/s in air at a place where g = 9.8 m/s2. The sphere is taken in a gravity free hall having air at the same pressure and pushed down at a speed of 20 m/s.
(A) its initial acceleration will be 9.8 m/s2 downward
(B*) its initial acceleration will 9.8 m/s2 upward
(C*) the magnitude of acceleration will decrease as the time passes
(D*) it will eventually stop
1. One end of a wire 2 m long and 0.2 cm2 in cross-section is fixed in a ceiling and a load of 4.8 kg is attached to the free end. Find the extension of the wire. Young’s modulus of steel = 2.0 × 1011
N/m2. Take g = 10 m/s2. HCV_Ch-14_WOE_1

2. One end of a nylon rope of length 4.5 m and diameter 6 mm is fixed to a tree-limb. A monkey weighing 100 N jumps to catch the free end and stays there.
Find the elongation of the rope and the corresponding change in the diameter. Young’s modulus of nylon = 4.8 × 1011 N/m2 and Poisson’s ratio of nylon = 0.2.

3. Two blocks of masses 1 kg and 2 kg are connected by a metal wire going over a smooth pulley as shown in figure. The breaking stress of the metal is 2 × 109 N/m2.
What should be the minimum radius of the wire used if it is not to break? Take g = 10 m/s2
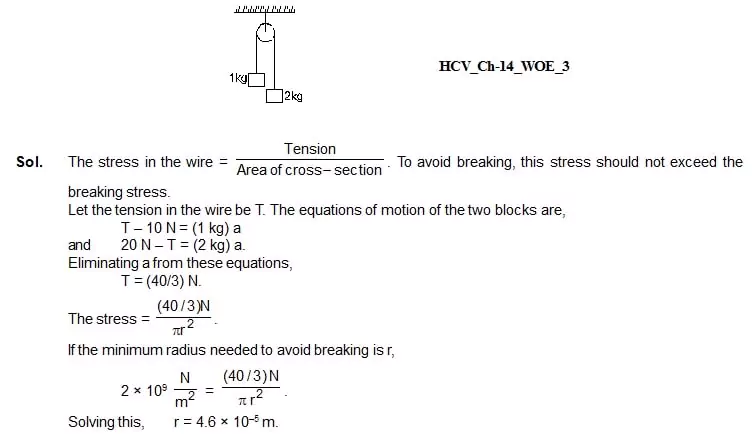
HCV_Ch-14_WOE_3

6. One end of a metal wire is fixed to a ceiling and a load of 2 kg hangs from the other end. A similar wire is attached to the bottom of the load and another
load of 1 kg hangs from this lower wire. Find the longitudinal strain in both the wires. Area of cross-section of each wire is 0.005 cm2 and Young’s modulus of
the metal is 2.0 × 1011 N/m2. Take g = 10 m/s2.

7. Each of the three blocks P, Q and R shown in figure has a mass of 3 kg. Each of the wires A and b has cross-sectional area 0.005 cm2 and
Young’s modulus 2 × 1011 N/m2. Neglect friction. Find the longitudinal strain developed in each of the wires. Take g = 10 m/s2.
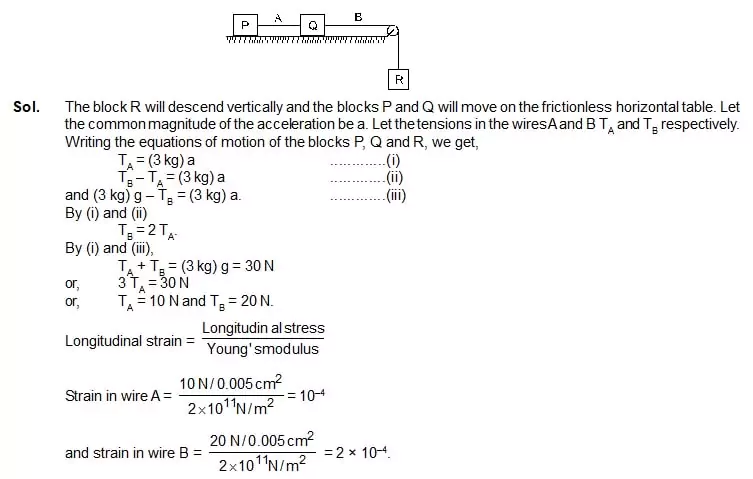
8. A wire of area of cross-section 3.0 mm2 and natural length 50 cm is fixed at one end and mass of 2.1 kg is hung from the other end. Find the elastic
potential energy stored in the wire in steady state. [Given : Young’s modulus of the material of the wire = 1.9 × 1011 N/m2. Take g = 10 m/s2.]

9. A block of weight 10 N is fastened to one end of a wire of cross-sectional area 3 mm2 and is rotated in a vertical circle of radius 20 cm. The speed of the block
at the bottom of the wire is 2 m/s. Find the elongation of the wire when the block is at the bottom of the circle. Young’s modulus of the material of the wire = 2 × 1011 N/m2.

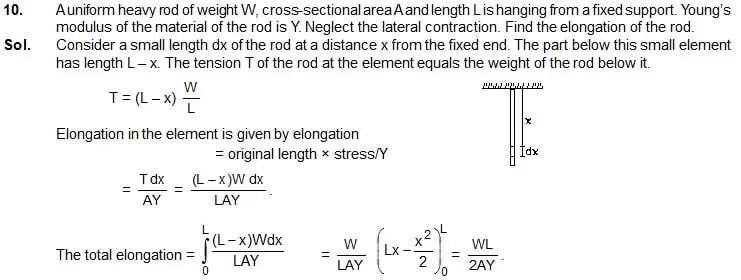
11. There is an air bubble of radius 1.0 mm in a liquid of surface tension 0.075 N/m and density 1000kg/m3. The bubble is at a depth of 10 cm below the free
surface. By what amount is the pressure inside the bubble greater than the atmospheric pressure ? Take g = 9.8 m/s2.
Sol. Let the atmospheric pressure be P0. The pressure of the liquid just outside the bubble is(figure)
12. A light wire AB of length 10 cm can slides on a vertical frames as shown in figure. There is a film of soap solution trapped between the frame and the wire.
Find the load W that should be suspended from the wire to keep it in equilibrium. Neglect friction. Surface tension of soap solution = 25 dyne/cm. Take g = 10 m/s2.

Sol. Soap solution film will be formed on both sides of the frame. Each film is in contact with the wire along a distance of 10 cm. The force exerted by the film on the wire
= 2 × (10 cm) × (25 dyne/cm)
= 500 dyne = 5 × 10–3 N.
This force acts vertically upward and should be balanced by the load. Hence the load that should be suspended is 5 × 10–3 N.
The mass of the load should be 5x10-3N/(10m/s2)= 5 × 10 kg = 0.5 g.
13. The lower end of a capillary tube is dipped into water and it is seen that the water rises through 7.5 cm in the capillary.
Find the radius of the capillary. Surface tension of water = 7.5 × 10–2 N/m. Contact angle between water and glass = 0°. Take g = 10 m/s2.
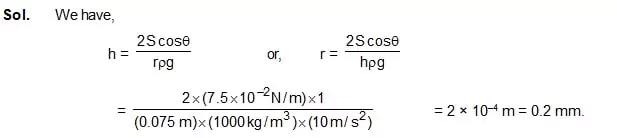
14. Two mercury drops each of radius r merge to form a bigger drop. Calculate the surface energy released.

15. A large wooden plate of area 10 m2 floating on the surface of a river is made to move horizontally with a speed of 2 m/s by
applying a tangential force. If the river is 1 m deep and the water in contact with the bed is stationary, find the tangential force needed to keep the plate moving.
[Coefficient of viscosity of water at the temperature of the river = 10–2 poise.]


17. Find the terminal velocity of a rain drop of radius 0.01 mm. The coefficient of viscosity of air is
1.8 × 10–5 N-s/m2 and its density is 1.2 kg/m3. Density of water = 1000 kg/m3. Take g = 10 m/s2.

1. A load of 10 kg is suspended by a metal wire 3 m long and having a cross-sectional area 4mm2. Find
(a) the stress (b) the strain and (c) the elongation. Young’s modulus of the metal is 2.0 × 1011 N/m2.
Ans. (a) 2.5 × 107 N/m2 (b) 1.25 × 10–4 (c) 3.75 ×10–4 m
2. A vertical metal cylinder of radius 2 cm and length 2m is fixed at the lower end and a load of 100 kg is put on it.
Find
(a) the stress (b) the strain and (c) the compression of the cylinder. Young’s modulus of the metal = 2 × 1011 N/m2.
Ans. (a) 7.96 × 105 N/m2 (b) 4 × 10–6 (c) 8 × 10–6 m
3. The elastic limit of steel is 8 × 108 N/m2 and its Young’s modulus 2 × 1011 N/m2. Find the maximum elongation of a half-meter steel wire that can be given without exceeding the elastic limit.
3. 2mm
4. A steel wire and a copper wire of equal length and equal cross-sectional area are joined end to end and the combination is subjected to a tension.
Find the ratio of (a) the stresses developed in the two wires and (b) the strains developed. Y of steel = 2 × 1011 N/m2. Y of copper = 1.3 × 1011 N/m2.
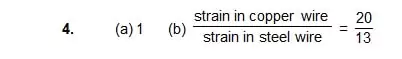
5. In the figure the upper wire is made of steel and the lower of copper. The wires have equal cross-section. Find the ratio of the longitudinal strains developed in the two wires.

6. The two wires shown in figure are made of the same material which has a breaking stress of
8 × 108 N/m2. The area of cross-section of the upper wire is 0.006 cm2 and that of the lower wire is 0.003 cm2.
The mass m1 = 10 kg, m2 = 20 kg and the hanger is light.
(a) Find the maximum load that can be put on the hanger without breaking a wire. Which wire will break first if the load is increased?
(b) Repeat the above part if m1 = 10 kg and m2 = 36 kg.

6. (a) 14 kg, lower (b) 2 kg, upper
7. Two persons pull a rope towards themselves. Each person exerts a force of 100 N on the rope.
Find the Young’s modulus of the material of the rope if it extends in length by 1 cm.
Original length of the rope = 2 m and the area of cross-sectional = 2 cm2.
7. 1 × 108 N/m2
8. A steel rod of cross-sectional area 4 cm2 and length 2 m shrinks by 0.1 cm as the temperature decreases in night.
If the rod is clamped at both ends during the day hours, find the tension developed in it during night hours. Young’s modulus of steel = 1.9 × 1011 N/m2.
8. 3.8 × 106 N
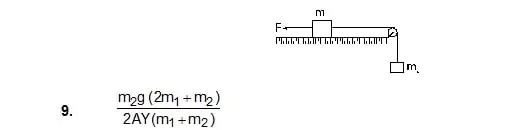
9. Consider the situation shown in figure. The force F is equal to the m2g/2. If the area of cross-section of the string is A and its Young’s modulus Y,
find the strain developed in it. The string is light and there is no friction anywhere.
10. A sphere of mass 20 kg is suspended by a metal wire of unstretched length 4 m and diameter 1 mm. When in equilibrium, there is a clear gap of
2 mm between the sphere and the floor. The sphere is gently pushed aside so that the wire makes an angle Theta with the vertical and is released.
Find the maximum value of Theta so that the sphere does not rub the floor. Young’s modulus of the metal of the wire is 2.0 × 1011 N m2.
Make appropriate approximations.
10. 36.4°
11. A steel wire of original length 1 m and cross-sectional area 4.00 mm2 is clamped at the two wneds so that it lies horizontally and without tension.
If a load of 2.16 kg is suspended from the middle point of the wire, what would be its vertical depression ?
Y of the steel = 2.0 × 1011 N/m2. Take g = 10 m/s2.
11. 1.5 cm
12. A copper wire of cross-sectional area 0.01 cm2 is under a tension of 20 N. Find the decrease in the cross-sectional area. Young’s modulus of copper = 1.1 × 1011 N/m2 and Poisson’s ratio = 0.32.
![]()
12. 1.164 × 10–6 cm2
13. Find the increase in pressure required to decrease the volume of a water sample by 0.01%. Bulk modulus of water = 2.1 × 109 N/m2.
13. 2.1 × 106 N/m2
14. Estimate the change in the density of water in ocean at a depth of 400 m below the surface. The density of water at the surface = 1030 kg/m3 and the bulk modulus of water = 2 × 109 N/m2.
14. 2 kg/m3
15. A steel plate of face-area 4 cm2 and thickness 0.5 cm is fixed rigidly at the lower surface. A tangential force of 10 N is applied on the upper surface.
Find the lateral displacement of the upper surface with respect to the lower surface. Rigidity modulus of steel = 8.4 × 1010 N/m2.
15. 1.5 × 10–9 m
16. A 5.0 cm long straight piece of thread is kept on the surface of water. Find the force with which the surface on one side of the thread pulls it. Surface tension of water = 0.076 N/m.
16. 3.8 × 10–3 N
17. Find the excess pressure inside
(a) a drop of mercury of radius 2 mm
(b) a soap bubble of radius 4 mm and
(c) an air bubble of radius 4 mm formed inside a tank of water. Surface tension of mercury, soap solution and water are 0.465N/m, 0.03 N/m and 0.076 N/m respectively.
17. (a) 465 N/m2 (b) 30 N/m2 (c) 38 N/m2
18. Consider a small surface area of 1 mm2 at the top of a mercury drop of radius 4.0 mm. Find the force exerted on this area
(a) by the air above it
(b) by the mercury below it and
(c) by the mercury surface in contact with it. Atmospheric pressure = 1.0 × 105 Pa and surface tension of mercury = 0.465 N/m. Neglect the effect of gravity. Assume all numbers to be exact.
18. (a) 0.1 N (b) 0.10023 N (c) 0.00023 N
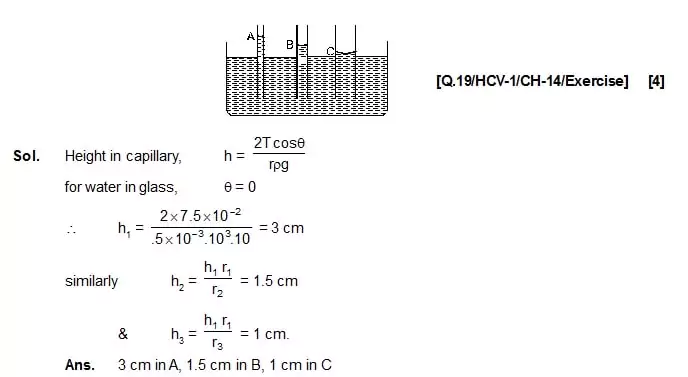
19. The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water.
Find the heights of water level in the capillaries. [Given the surface tension of water is 7.5 × 10–2 N/m.]
20. The lower end of a capillary tube is immersed in mercury. The level of mercury in the tube is found to be 2 cm below the outer level.
If the same tube is immersed in water, upto what height will the water rise in the capillary?
20. 5.73 cm
21. A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape.
If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube. The contact angle of
mercury with glass = 135° and surface tension of mercury = 0.465 N/m. Density of mercury = 13600 kg/m3.
21. 75.5 cm
22. A capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in
the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water = 0.075 N/m.
22. 190 N/m2
23. Find the surface energy of water kept in a cylindrical vessel of radius 6.0 cm. Surface tension of water = 0.75 J/m2.
23. 8.5 × 10–4 J
24. A drop of mercury of radius 2 m is split into 8 identical droplets. Find the increase in surface energy. Surface tension of mercury = 0.465 J/m2.
24. 23.4 µJ
25. A capillary tube of radius 1 mm is kept vertical with the lower end in water.
(a) Find the height of water raised in the capillary.
(b) If the length of the capillary tube is half the answer of part (a), find the angle q made by the water surface in the capillary with the wall.
25. (a) 1.5 cm (b) 60°
26. The lower end of a capillary tube of radius 1 mm is dipped vertically into mercury.
(a) Find the depression of mercury column in the capillary.
(b) If the length dipped inside is half the answer of part (a), find the angle made by the mercury surface at the end of the capillary with the vertically.
Surface tension of mercury = 0.465 N/m and the contact angle of mercury with glass = 135°.
26. (a) 5.34 mm (b) 112°’
27. Two large glass plates are placed vertically and parallel to each other inside a tank of water with separation between the plates equal to 1 mm.
Find the rise of water in the space between the plates. Surface tension of water = 0.075 N/m.
27. 1.5 cm
28. Consider an ice cube of edge 1.0 cm kept in a gravity free hall. Find the surface area of the water when the ice melts.
Neglect the difference in densities of ice and water.
28. (36 pie)1/3 cm2
29. A wire forming a loop is dipped into soap solution and taken out so that a film of soap solution is formed. A loop of 6.28 cm
long thread is gently put on the film and the film is pricked with a needle inside the loop. the thread loop takes the shape of a circle.
Find the tension in the thread. Surface tension of soap solution = 0.030 N/m.
29. 3 × 10–4 N
30. A metal sphere of radius 1 mm and mass 50 mg falls vertically in glycerine.
Find (a) he viscous force exerted by the glycerine on the sphere when the speed of the sphere is 1 cm/s,
(b) the hydrostatic force exerted by the glycerine on the sphere and
(c) the terminal velocity with which the sphere will move down without acceleration.
Density of glycerine - 1260 kg/m3 and its coefficient of viscosity at room temperature = 8.0 poise
30. (a) 1.5 × 10–4 N (b) 5.2 × 10–5 N (c) 2.9 cm/s
31. Estimate the speed of vertically falling raindrops from the following data. Radius of the drops = 0.02 cm,
viscosity of air = 1.8 × 10–4 poise, g = 9.9 m/s2 and density of water = 1000 kg/m3.
31. 5 m/s
32. Water flows at a speed of 6 cm/s through a tube of radius 1 cm. Coefficient of viscosity of water at room
temperature is 0.01 poise. Calculate the Reynolds number. Is it a steady flow?
32. 120, yes