1. A particle moves in a circle of radius 20 cm with a linear speed of 10 m/s. Find the angular velocity.
Sol. The angular velocity is
![]()
2. A particle travels in a circle of radius 20 cm at a speed that uniform increses. If the speed changes from 5.0 m/s to 6.0 m/s in 2.0s, find the angular acceleration.
Sol. The tangentical accelaration is given by
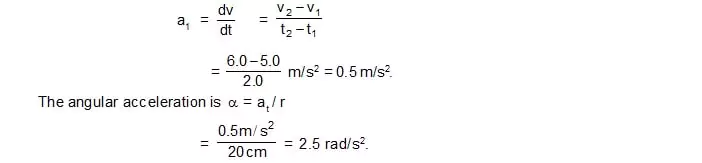
3. Find the magnitude of the linear acceleration of a particle moving in a circle of radius 10 cm with uniform speed completing the circle in 4s.
Sol. The distance covered in completing the circle is 2r = 2 × 10 cm.The linear speed is
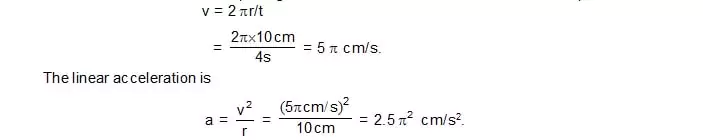
4. A particle moves in a circle of radius 20 am. Its linear speed is given by v = 2t where t is in second and v in meter/second . Find the radical and tangential acceleration at t = 3s.
Sol. The linear speed at t = 3s is
v = 2t = 6 m/s.
The radical acceleration at t = 3s is
ar = v2 / r = 36/0.20 = 180 m/s2.
The tangent acceleration is
at =dv/dt = d(2t)/dt = 2 m/s2.
5. A small block of mass 100 g moves with uniform speed in a horizontal circular groove, with vertical side walls , of radius 25 cm. If the block takes 2.0s to complete one round, find the normal contact force by the slide wall of the groove.
Sol. The speed of the block is

6. The road at a circular turn of radius 10m is banked by an angle of 10º. With what speed should a vehicle move on the turn so that the normal contact force is able to provide the necessary force ?
Sol. If v is the correct speed
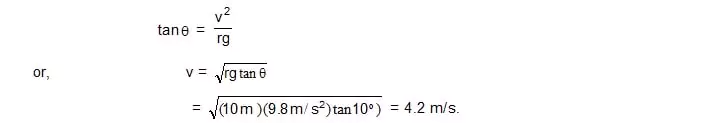
7. A body weighs 98N on a spring balance at the north pole. What will be its weight recorded on the same scale if it is shifted to the equator? Use g = GM/R2 = 9.8 m/s2 and the radius of the earth R=6400 km.
Sol. At poles , the apparent weight is same as the true weight.
Thus,

1. You are driving a moorcycle on a horizontal road. It is moving with a uniform velocity. Is it possible to accelerate the motorcycle without putting higher petrol input rate into the engine ?
2. Some washing machines have cloth driers. It contains a drum in which wet clothes are kept. As the drum rotates, the water particles get separated from the cloth. The genral description of this action is that “the contrifugal force throws the water particles away from the drum”. Comment on this statement from the view-point of an observer rotating with the drum and the observer who is washing the clothes. 
6. After a good metal at a party you wash your hands and find that you have forgotten to bring your handker chief.
7. A smooth block loosely fits in a circular tube placed on a horizontaly surface. The block moves in a uniform circular motion along the tube (figure). Which wall (inear or outer) will exert a nonzero normal contact force on the the block?
8. Consider the circular motion of the earth around the sun. Which of the following statements is more appropriate ?
(A) Gravitional attraction of the sun on the earth is equal to the centripetal force.
(B) Gravitional attraction of the sun on the earth is the centripetal force.
9. A car driver going at some speed v suddenly finds a wide wall at a distance r.Should he apply brakes or turn the car in a circle of radius r to avoid hitting the wall?
10. A heavy mass m is hanging from a string in equilibrium without breaking it.When this same is set into oscillation , the string breaks. Explain.
1. When a particle moves in a circle with a uniform speed
(A) its velocity and acceleration are both constant
(B) its velocity is constant but the acceleration changes
(C) its acceleration is constant but the velocity changes
(D*) its velocity and acceleration both change
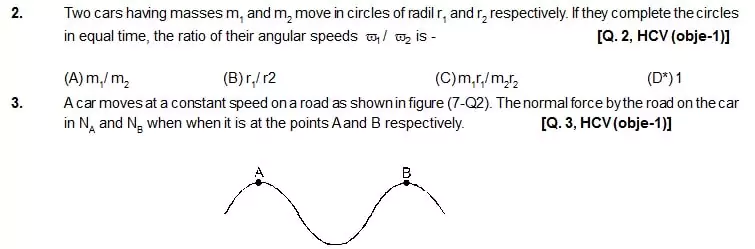
(A) NA = NB (B) NA > NB (C*) NA < NB (D) insufficient
4. A particle of mass m is observed from an inertial frame of reference and is found to move in a circle of radius r with a unifrom speed v. The centrifugal force on it is
(A) towards the centre (B) away from the centre
(C) along the tangent through the particle (D*) zero k

6. A particle is kept fixed on a turnatable rotating uniformly. As seen from the ground , the particle goes in a circle , its speed is 20 cm/ss and acceleration is 20 cm/s2.The particle is now shifted to a new position to make the radius half of the original value.The new values of the speed and acceleration will be
(A*) 10 cm/s, 10 cm/s2 (B) 10 cm/s, 80 cm/s2 (C) 40 cm/s, 10 cm/s2 (D) 40 cm/s,40 cm/s2
7. Water in a bucket is whirled in a vertical circle with a string attached to it.The water does not fall down even when the bucket is inverted at the top of its path. We conclude that in this position.
(A) mg = mv2/r (B) mg is greater than mv2/r
(C*) mg is not greater than mv2/r (D) mg is not less than mv2/r
8. A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre.The speed of the stone is v. If the string bresks, the stone will move -
(A) towards the centre (B) away from the centre (C*) along a tangent (D) will stop
9. A coin placed on a rotating turntable just slips if is placed at a distance of 4 cm from the centre. if the angular velocity of the turntable is doubled , it will just slip at a distance of
(A*) 1 cm (B) 2 cm (C) 4 cm (D) 8 cm
10. A motorcycle is going on an overbridge of radius R. The driver maintains a constant speed. As the motorcycle is ascending on the overbrdge, the normal force on it -
(A*) increases (B) decreases (C) remains the same (D) flutuates
11. Three identical cars, A, B and C are moving at the same speed on three bridges.The car A goes on a plane bridge B on a bridge convex upward and C goes on a bridge concave upward. Let FA, FB and FC be the normal forces exerted by the cars on the bridges when they are at the middle of bridges.
(A) FA is maximum of the three forces. (B) FB is maximum of the three forces.
(C*) FC is maximum of the three forces (D) FA = FB = FC
12. A train A runs from east to west and another train B of the same mass runs from west to east at t he same speed along the equator. A presses the track with a force F1 and B presses the track with a force F2.
(A*) F1 > F2
(B) F1 < F2
(C) F1= F2
(D) the information is insufficient to find the relation between F1 and F2.
13. If the earth stops , rotating the apparent value of g on its surface will
(A) increase everywhere
(B) decrease everywhere
(C) remain the same everywhere
(D*) increase at some places and remain the same at some other places
14. A rod of length L is pivoted at one end and is rotated with a uniform angular velocity in a horizontal plane . Let T1 and T2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends. [Q. 14, HCV (obje-1)]
(A*) T1 > T2 (B) T2 > T1
(C) T1 = T2
(D) The relation between T1 and T2 depends on whether the rod rotates clockwise or anticlockwise
15. A simple pendulum having a bob of mass m is suspended from the ceiling of a car used in a stunt film shotting . The car moves up along an inclined cliff at a speed v and makes a jump to leave the cliff and lands at some distance . Let R be the maximum height of the car from the top of the cliff. The tension is the string when the car is in air is

16. Let doenote the angular displacement of a simple pendulam oscillating in a vertical plane. If the mass of the bob is m, the tension in the string is mgcos
(A) always
(B) never
(C*) at the extereme positions
(D) at the mean position
1. An object follows a curved path. The following quantities may remain during the motion -
[Q. 1, HCV (obje-2)]
(A*) speed (B) velocity (C) acceleration (D*) magnitude of acceleration
2. Assume that the earth goes round the sun in a circular orbit with a constant speed of 30 km/s.
(A) The average velocity of the earth from 1st Jan , 90 to 30th June , 90 is zero [Q. 2, HCV (obje-2)]
(B) The average acceleration during the above period is 60 km/s2.
(C) The average speed from 1st Jan , 90 to 31st Dec, 90 is zero.
(D*) The instantaneous acceleration of the earth points towards the sun.
3. The position vector of a particle in a circular motion about the origin sweeps out equal area in equal time. Its
(A) velocity remains constant (B*) speed remains constant [Q. 3, HCV (obje-2)]
(C) acceleration remains constant (D*) tangential acceleration remains constant
4. A particle is going in a spiral path as shown in figure (7-Q3) with constant speed. [Q. 4, HCV (obje-2)]
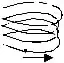
(A) The velocity of the particle is constant
(B) The acceleration of the particle is constant
(C*) The magnitude of accleration is constant
(D) The magnitude of accleration is decreasing continuously
5. A car of mass M is moving on a horizontaly on a circular path of radius r. At an instant its speed is v and is increasing at a rate a. [Q. 5, HCV (obje-2)]
(A) The acceleration of the car is towards the centre of the path
(B*) The magnitude of the frictional force on the car is greater than mv2/r
(C*) The friction coefficient between the ground and the car is not less than a/g.
(D) The friction coefficient between the ground and the car is mew= tan– 1 v2/rg
6. A circular road of radius r is banked for a speed v = 40 km/hr. A car of mass attempts to go on the circular road. The friction coefficient between the tyre and the road is negligible . [Q. 6, HCV (obje-2)]
(B*) If the car turns at a speed less than 40 km/hr, it will slip down
(C) If the car turns at the current speed of 40 km/hr, the force by the road on the car is equal mv2/r
(D*) If the car turns at the correct speed of 40 km/hr, the force by the road on the car is greater than mg as well as greater than mv2/r
7. A person applies a constant force on a particle of mass m and finds that the particle moves in a circle of radius r with a uniform speed v as seen from an inertial frame of reference. [Q. 7, HCV (obje-2)]
(A) This is not possible.
(B*) There are other forces on the particle
(C) The resultant of the other forces is towards the centre.
(D*) The resultant of the other forces varies in magnitude as well as in direction.


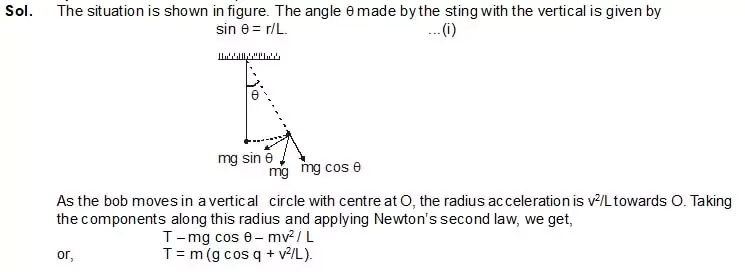
3. A particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r. Find (a) the speed of the particle and (b) the tension in the string. Such a system is called a conical pendulum.
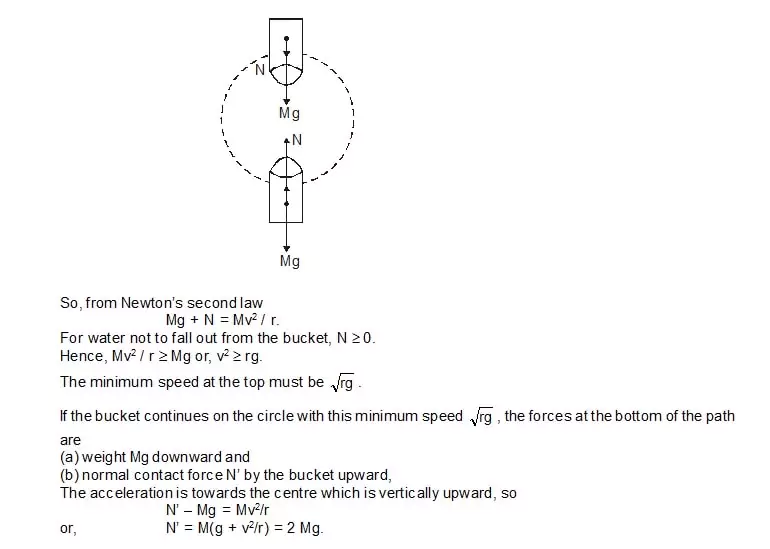
6. A cylindrical filled with watger is whirled around in a vertical circle of radius r. What can be the minimum speed at the top of the parth if water does not fall out from the bucket/ If it continues with this speed, what normal contact froce the bucket exerts on water at the lowest point of the path?
Sol. Consider water as the system. At the top of the circle its acceleration towards the centre is verrtically downward with magnitude v2/r. The forces on water are (figure).
(a) weight Mg downward and
(b) normal force by the bucket, also downward.
7. A fighter plane is pulling out for a dive at a speed of 900 km/hr. Assuming its path to be vertical circle of radius 2000 m and its mass to be 16000 kg, find the force exeerted by the air an it at the lowest point. Take g = 9.8 m/s2.
Sol. At the lowest point in the path the acceleration is vertically upward (towards the centre) and its magnitude is v2/r.
The forces on the plane are
(a) weight Mg downward and
(b) force F by the air upward.
Hence, Newton’s second loaw of motion gives
F – Mg = Mv2/r
or, F = M(g + v2/r).
Here v = 900 km/hr = (900000/3600) m/s = 250 m/s
or, F = 16000 (9.8+62500/2000) N = 6.56 × 10 5 N (upward).
8. Figure shows a rod of length 20 cm pivoted near an end and which is made to rotate in a horizontal plane with a constant angular speed. A ball of mass m is suspended by a string also of length 20 cm from the other end of the rod. If the angle q made by the string with the vertical is 30º, find the angular speed of the rotation. Take g = 10 m/s2.
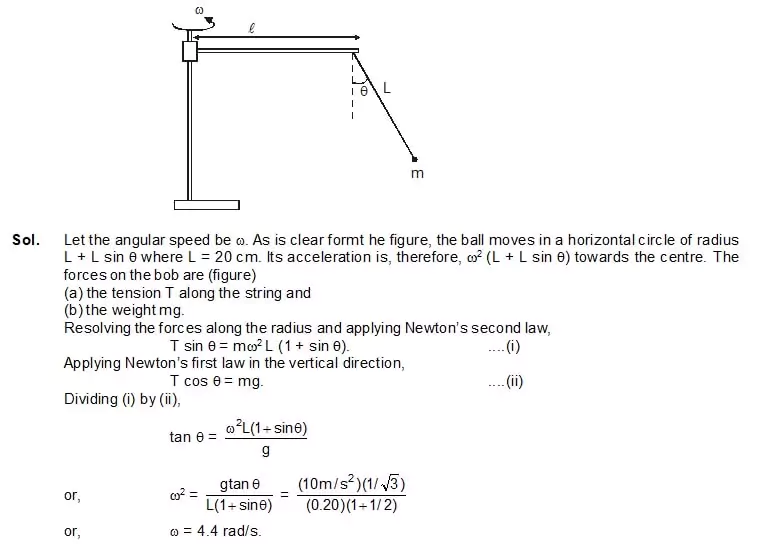
9. Two blocks each of mass M are connected to the ends of a light frame as shown in figure. The frame is rotated about the vertical line of symmetry. The rod breaks if the tension in it exceeds T0. The rod breaks if the tension in it exceeds T0. Find the maximum frequency with which the frame may be rotated without breaking the rod.
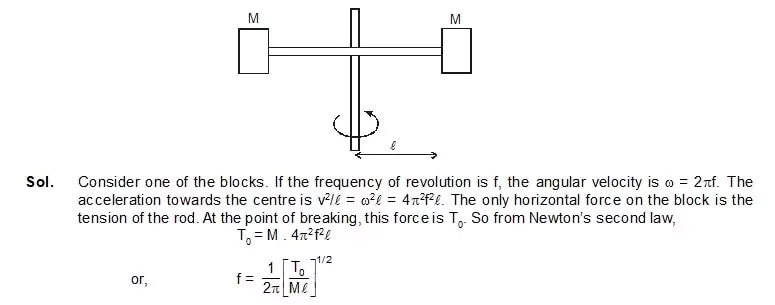
10. In a rotor, a hollow vertical cylindrical structure rotates about its axis and a person rests against the inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hange resting oaginst thw wall without any floor. If the radius of the rotor is 2m and the coefficient of static friction between the wall and the person is 0.2, find the minimum speed at which the floor may be removed. Take g = 10 m/s2
Sol. The situation is shown in figure.
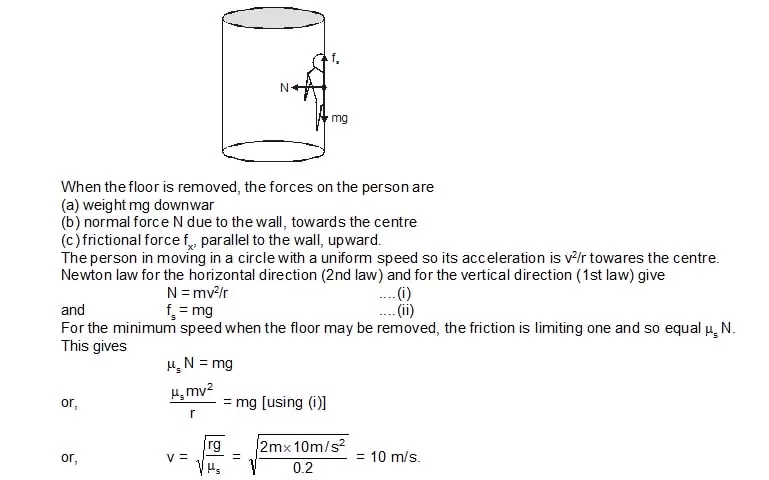
11. A hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surface of the bowl is smooth, and the angle made by the radius through the block with the vertical is q. find the angular speed at which the bowl is rotating.
Sol. Suppose the angular speed of rotation of the bowl is w. The block also moves with this angular speed. The forces on the block are (figure).
(a) the normal force N and
(b) the weight mg.
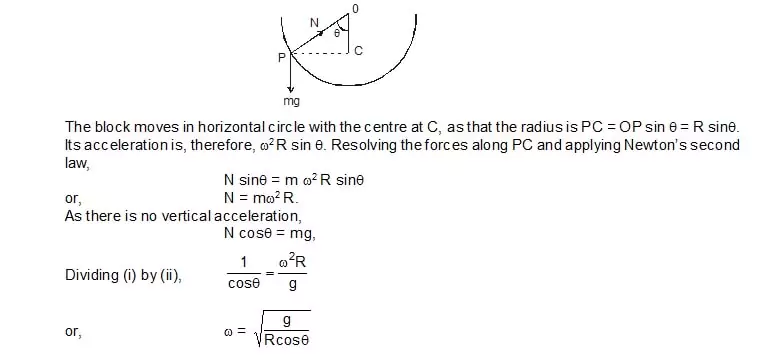
12. A metal ring of mass m and radius R is place on a smooth horizontal table and is set rotating about its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
Sol. Consider a small part ACB of the ring the subtends an angle Dq at the centre as shown in figure. Let the tension in the ring be T.
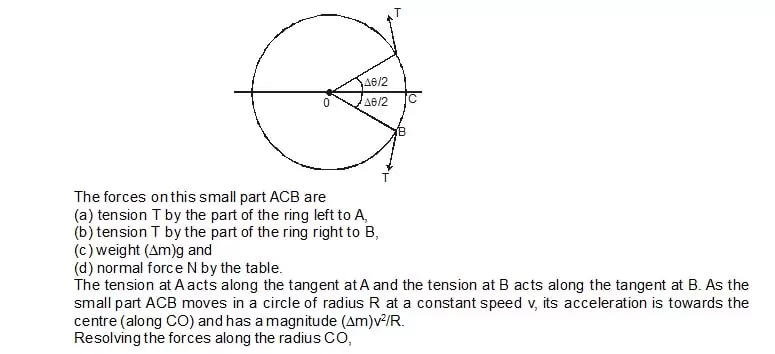
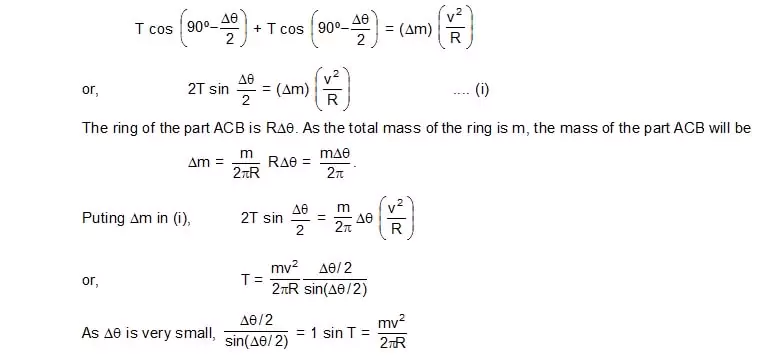
13. A table with smooth horizontal surface is turning at an angular speed w about its axis. A groove is made on the surface along a radius and a particlis gently placed inside the groove at a distance a from the centre. Find the speed of the particle with respect to the table as its distance from the centre becomes L.
Sol. The situation is shown in figure.
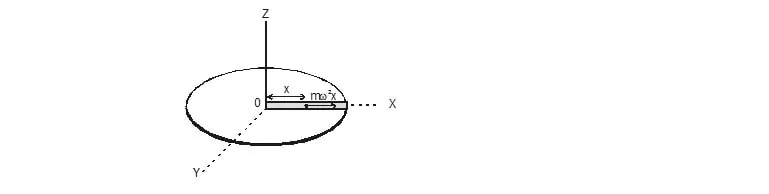
Let us work from the frame of reference of the table. Let us take the origin at the centre of rotation O and the X-axis along the groove (figure). The Y-axis is along the line perpendicular to OX, coplanar with the surface of the table and the Z-axis is along the vertical. Suppose at time t the particle in the groove is at a distance x from the origin and is moving along the X-axis with a speed v. The forces acting on the particle (including the pseudo forces that we must assume because we have taken our frame on the table which is rotating and is nonintertial) are

1. Find the acceleration of the moon with respect to the earth from the following data :Distance between the earth and the moon = 3.85 × 105 km and the time taken by the moon to complete one
revolution around the earth = 27.3 days. [Ans : 2.73 × 10–3 m/s2]
2. Find the acceleration of a particle placed on the surface of the earth at the equator due to earth’s rotation. The diameter of earth = 12800 km and it takes 24 hours for the earth to complete one revolution about its axis. [Ans : 0.0336 m/s2]
3. A particle moves in a circle of radius 1.0 cm at a speed given by v= 2.0 t where v is in cm/s and t in seconds.
(A) Find the radial acceleration of the particle at t = 1s.
(B) Find the tangential acceleration at t = 1s
(C) Find the magnitude of the acceleration at t = 1s.
[Ans : (A) 4.0 cm/s2 , (B) 2.0 cm/s2, (C) cm/s2]
4. A scooter weighing 150 kg toghter with its rider moving at 36 km/hr is to take a turn. of radius 30 m. What horizontal force on the scooter is needed to make the turn possible? [Ans : 500 N]
5. If the horizontal force needed for the turn in the previous problem is to be supplied by the normal force by the road,what should be the proper angle of banking ? [Ans : tan–1(1/3) ]
6. A park has a radius of 10m. If a vehicle goes round it at an average speed of 18 km/hr , what should be the proper angle of banking? [Ans : tan–1(1/4)]
7. If the road of the previous problem is horizontal (no banking) , what should be the minimum friction coefficient so that a scotter going at 18 km/hr does not skid. [Ans : 0.25]
8. A circular road of radius 50 m has the angle of banking equal to 30º. At what speed should a vehicle go on this road so that the friction is not used? [Ans : 17 m/s ]
9. In the Bohr model of hydrogen atom, the electron is treated as a particle going in a circle with the centre at the proton. The proton itself is assumed to be fixed in an inertaial frame. The centripetal force is provided by the Coloumb attraction. In the ground state, the electron goes round the proton in a circle of radius 5.3 × 10–11 m. Find the speed of the electron in the ground state. Mass of the electron = 9.1 × 10–31 kg and charge of the electron = 1.6 × 10–19 C.
[Ans : 2.2 × 106 m/s]
10. A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the miniumum speed the stone can have at the highest point of the circle.
![]()
11. A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1g sticking at the outer end of a blade. How much forcedoes it experience when the fan runs at full speed ? Who exerts this force on the particle ? How much force does the particle exert on the blade along its surface ? [Ans : 14.8N, 14.8 N]

13. A simple pendulum is suspended from the celling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by the string of the pendulum with the vertical if this angle does not change during the turn. Take g = 10 m/s2. [Ans : 45º]
14. The bob of a simple pendulum of length 1m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the string at this instant. [Ans : 1.2 N]
.webp)
16. Suppose the amplitude of a simple pendulum having a bob of mass m is theta not. Find the tension in the string when the bob is atn its exterme position.
17. A person stands on a spring balance at the equator. (A) By what fraction is the balance reading less than his true weight ? (B) If the speed of earth’s rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case ?
[Ans : (A) 3.5 × 10–3, (B) 2.0 hour]
18. A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that is neither slips down nor skids up ? [Ans : Between 14.7 km/h and 54 km/hr]
19. A motorycle has to move with a constant speed on an overbridge which is in the form a circular are of radius R and has a total length L. Suppose the motorcycle starts from the highest point (A) What can its maximum velocity be for which the contact with the road is not broken at the highest point? (B) If the motorcycle goes at speed 1 / times the maximum found in part (A), where will it lose the contact with the road ? (C) What maximum uniform speed can it maintain on the bridige if it does not lose contact anywhere on the on the bridge ?
![]()

 21. A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is m. The ruler
21. A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is m. The ruler
22. A track consists of two circular parts ABC and CDE of equal radius 100 m and joined smoothly as shown in fig. Each part subtends a right angle at its centre. A cycle weighing 100 kg together with the rider travels at a constant speed of 18 km/h on the rack. (A) Find the normal contact force by the road on the cycle when it is at B and D. (B) Find the corce of friction exerted by the track on the types when the cycle is at B, C and D. (e) Find the normal force between the road and the cycle just, becore and just after the cycle crosses C. (D) What should be the minimum friction coefficient between the road and the type, which will ensure that the cyclist can move with constant speed ? Take g = 10m/s2.

[Ans : (A) 975N, 1025 N , (B) 0,707N, 0 , (C) 682N , 732 N , (d ) 0 1.037]
23. In a children’s park a heavy rod is pivoted at the centre and is moade to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod (fig.). Let the mass of eachkid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.

24. a hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical. A small block is kept in the bowl at a position where the radius makes ang angle q with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl without any slipping . The friction coefficient between the block and the bowl surface is mew . Find the range of the angualr speed for which the block will not slip.
 [Ans : to ]
[Ans : to ] 
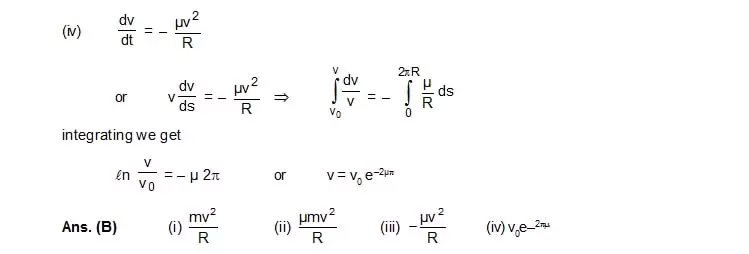
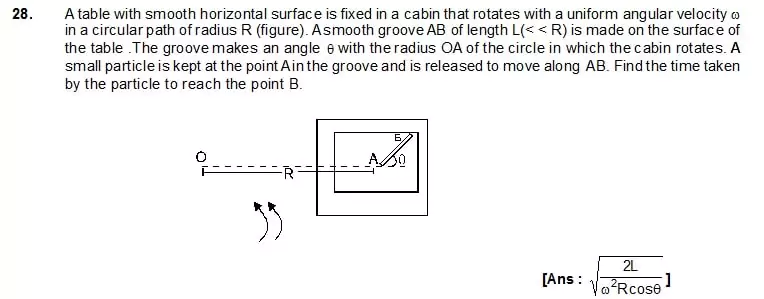
29. A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wodden plate is kept on the seat with its plane perpendicular to the radius of the circular road figure. A small block of mass 100g is kept on the seat which rests against the plate. The friction coefficient between the block and the plate is = 0.58.
(A) Find the normal contact force exerted by the plate on the block.
(B) The plate is slowly turned so that the angle between the normal to the plate and radius of the angle between the normal to the plate and the radius of the road slowly increases. Find the angle at which the block will just start sliding on the plate.
30. A table with smooth horizontal surface is placed in a cabin which moves in a circle of a large radius R (figure). A smooth pulley of small radius is fastended to the table. Two masses m and 2m placed on the table are conneted through a string over the pulley. Initially the masses are held by a person with the string along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
