1. Two particles of masses 1.0 kg and 2.0 kg are placed at a separation of 50 cm. Assuming that the only forces acting on the particles are their mutual gravitation, find the initial accelerations of the two particles.
Sol. The force of gravitation exerted by one particle on another is

2. Find the work done in bringing three particles, each having a mass of 100 g, from large distances to the vertices of an equilateral triangle of side 20 cm.
Sol. When the separation are large, the gravitational potential energy is zero. When the particles are brought at the vertices of the triangle ABC, three pairs AB, BC and CA are formed. The potential energy of each pair is – Gm1m2/r and hence the total potential energy becomes
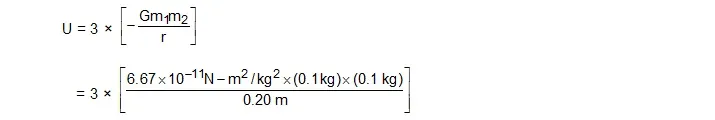
= – 1.0 × 10–11 J.
The work done by the gravitational forces is W = – U = 1.0 × 10–11 J. If the particles are brought by some external agency without changing the kinetic energy, the work done by the external agency is equal to the change in potential energy = – 1.0 × 10–11 J.
3. A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a/2 from the centre.
Sol. The gravitational potential at the point P due to the particle at the centre is
V1 = –GM/(a/2) = –2GM/a .
The potential at P due to the shell is
V2 = –GM/a
The net potential at P is V1 + V2 = – .3GM/a
4. A particle of mass 50 g experiences a gravitational force of 2.0 N when placed at a particular point. Find the gravitational field at that point.
Sol. The gravitational field has a magnitude

5. The gravitational field due to a mass distribution is given by E = K/x3 in X-direction. Taking the gravitational potential to be zero at infinity, find its value at a distance x. HCV_Ch-11_Sol.Ex._5
Sol.The potential at a distance x is

7. Find the gravitational field due to the moon at its surface. The mass of the moon is 7.36 × 1022 kg and the radius of the moon is 1.74 × 106 m. Assume the moon to be a spherically symmetric body.
Sol. To calculate the gravitational field at an a external point, the moon may be replaced by a single particle of equal mass placed at its centre. Then the field at the surface is

8. Calculate the value of acceleration due to gravity at a point (a) 5.0 km above the earth’s surface and (b) 5.0 km below the earth’s surface. Radius of earth = 6400 km and the value of g at the surface of the earth is 9.80 m/s2.

9. A satellite is revolving round the earth at a height of 600 km. Find (a) the speed of the satellite and (b) the time period of the satellite. Radius of the earth = 6400 km and mass of the earth = 6 × 1024 kg.
Sol. The distance of the satellite from the centre of the earth is 6400 km + 600 km = 7000 km.
The speed of the satellite is

10. Calculate the escape velocity from the moon. The mass of the moon = 7.4 × 1022 kg and radius of the moon = 1740 km.
Sol. The escape velocity is
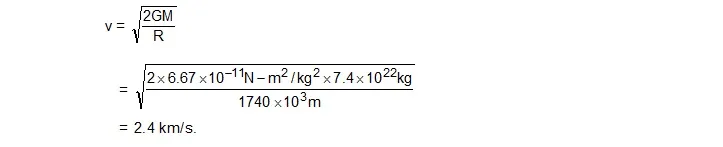
1. Three particles A, B and C, each of mass m, are placed in a line with AB = BC = d. Find the gravitational force on a fourth particle P of same mass, placed at a distance d from the particle B on the perpendicular bisector of the line AC.
Sol. The force at P due to A is

2. Find the distance of a point from the earth’s centre where the resultant gravitational field due to the earth and the moon is zero. The mass of the earth is 6.0 × 1024 kg and that of the moon is 7.4 × 1022 kg. The distance between the earth and the moon is 4.0 × 105 km.
Sol. The point must be on the line joining the centres of the earth and the moon and in between them. If the distance of the point from the earth is x, the distance from the moon is (4.0 × 105 km-x). The magnitude of the gravitatiional field due to the earth is

3. Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
Sol. The particles will always remain diametrically opposite so that the force on each particle will be directed along the radius. Consider the motion of one of the particles. The force on the particle is F = Gm2/4R2 . If the speed is v, its acceleration is v2/R.
Thus, by Newton’s law,

4. Two particles A and B of masses 1 kg and 2 kg respectively are kept 1 m apart and are released to move under mutual attraction. Find the speed of A when that of B is 3.6 cm/hour. What is the separation between the particles at this instant ?
Sol. The linear momentum of the pair A + B is zero initially. As only mutual attraction is taken into account, which is internal when A + B is taken as the system, the linear momentum will remain zero. The particles move in opposite directions. If the speed of A is v when the speed of B is 3.6 cm/hour = 10–5 m/s,
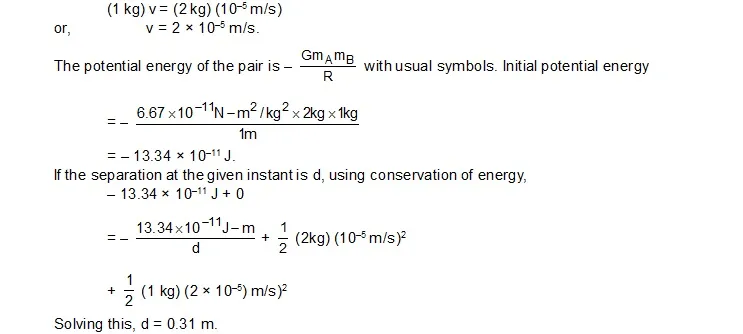
5. The gravitational field in a region is given by = (10 N/kg) ( i+ j). Find the work done by an external agent to slowly shift a particle of mass 2 kg from the point (0, 0) to a point (5m, 4m).
HCV_Ch-11_WOE_5
Sol. As the particle is slowly shifted, its kinetic energy remains zero. The total work done on the particle is thus zero. The work done by the external agent should be negative of the work done by the gravitational field. The work done by the field is

Thus, the total work done by the field, as the particle is shifted from O to B, is 180 J.
The work done by the external agent is – 180 J.
Note that the work is independent of the path so that we can choose any path convenient to us from O to B.

6. A uniform solid sphere of mass M and radius a is surrounded symmetrically by a uniform thin spherical shell of equal mass and radius 2 a. Find the gravitational field at a distance (a) 1.5a from the centre, (b) 5/2 a from the centre.

7. The density of mass inside a solid sphere of radius a is given by r = r0 a/r where r0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
Sol. The field is required at a point outside the sphere. Dividing the sphere in concentric shells, each shell can be replaced by a point particle at its centre having mass equal to the mass of the shell. Thus, the whole sphere can be replaced by a point particle at its centre having mass equal to the mass of the given sphere. If the mass of the sphere is M, the gravitational field at the given point is
E = = . ...........(i)
The mass M may be calculated as follows. Consider concentric shell of radius r and thickness dr. Its volume is
dV = (4pr2) dr
and its mass is
dM = rdV = (4pr2dr) = 4pr0 ar dr.
The mass of the whole sphere is
M = = 2pr0a3.
Thus, by (i) the gravitational field is
E = = pGr0a.
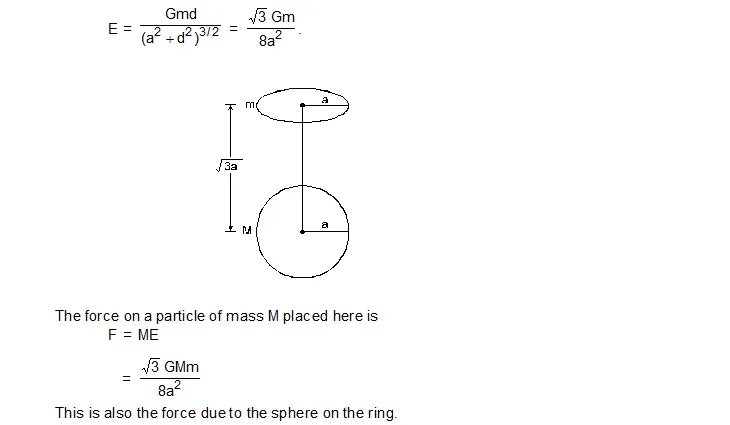
8. A uniform ring of mass m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance 1.732 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
Sol. The gravitational field at any point on the ring due to the sphere is equal to the field due to a single particle of mass M placed at the centre of the sphere. Thus, the force on the ring due to the sphere is also equal to the force on it by a particle of mass M placed at this point. By Newton’s third law it is equal to the force on the particle by the ring. Now the gravitational field due to the ring at a distance d = a on its axis is
9. A particle is fired vertically upward with a speed of 9.8 km/s. Find the maximum height attained by the particle. Radius of earth = 6400 km and g at the surface = 9.8 m/s2. Consider only earth’s gravitation.

10. A particle hanging from a spring stretches it by 1 cm at earth’s surface. How much will the same particle stretch the spring at a place 800 km above the earth’s surface ? Radius of the earth = 6400 km.
Sol. Suppose the mass of the particle is m and the spring constant of the spring is k. The acceleration due

11. A simple pendulum has a time period exactly 2 s when used in a laboratory at north pole. What will be the time period if the same pendulum is used in a laboratory at equator ? Account for the earth’s rotation only. Take g =GM/R2 = 9.8 m/s2 and radius of earth = 6400 km.

12. A satellite is to revolve round the earth in a circle of radius 8000 km. With what speed should this satellite be projected into orbit? What will be the time period? Take g at the surface
= 9.8 m/s2 and radius of the earth = 6400 km.
.
13. Two satellites S1 and S2 revolve round a planet in coplanar circular orbits in the same sence. Their periods of revolution are 1 h and 8h respectively. The radius of the orbit of S1 is 104 km. When S2 is closest to S1, find (a) the speed of S2 relative to S1 and (b) the angular speed of S2 as observed by an astronaut in S1.


1. Can two particles be in equilibrium under the action of their mutual gravitational force? Can three particles be ? Can one of the three particles be ?
2. Is there any meaning of “Weight of the earth” ?
3. If heavier bodies are attracted more strongly by the earth, why don’t they fall faster than the lighter bodies?
4. Can you think of two particles which do not exert gravitational force on each other ?
5. The earth revolves round the sun because the sun attracts the earth. The sun also attracts the moon and this force is about twice as large as the attraction of the earth on the moon. Why does the moon not revolve round the sun ? Or does it ?
6. At noon, the sun and the earth pulls the objects on the earth’s surface in opposite directions. At midnight the sun and the earth pull these objects in same direction. Is the weight of an object, as mesured by a spring balance on the earth’s surface, more at midnight as compared to its weight at noon?
7. An apple falls from a tree. An insect in the apple finds that the earth is falling towards it with an acceleration g. Who exerts the force needed to accelerate the earth with this acceleration g?
8. Suppose the gravitational potential due to a small system is k/r2 at a distance r from it. What will be the gravitational field ? Can you think of any such system? What happens if there were negative masses?
9. The gravitational potential energy of a two-particle system is derived in this chapter as U = –Gm1m2/r . Does it follow from this equation that the potential energy for r = infinite must be zero ? Can we choose the potential energy for r = infinite to be 20 J and still use this formula ? If no, what formula should be used to calculate the gravitational potential energy at separation r ?
10. The weight of an object is more at the poles than at the equator. Is it benificial to pruchase goods at equator and sell them at the pole ? Does it matter whether a spring balance is used or an equal beam balance is used ?
11. The weight of a body at the poles is greater than the weight at the equator. Is it the actual weight or the apparent weight we are talking about ? Does your answer depend on whether only the earths rotation is taken into account or the flattening of the earth at the poles is also taken into account ?
12. If the radius of the earth decreases by 1% without changing its mass, will the acceleration due to gravity at the surface of the earth increase or decrease? If so, by what per cent?
13. A nut becomes loose and gets detached from a satellite revolving around the earth. Will it land on the earth ? If yes, where will it land? If no, how can an astronaut make it land on the earth ?
14. Is is necessary for the plane of the orbit of a satellite to pass through the centre of the earth?
15. Consider earth satellites in circular obrits. A geostationary satellite must be at a height of about 36000 km from the earth’s surface. Will any satellite moving at this height be a geostationary satellite ? Will any satellite moving at this height have a time period of 24 hours ?
16. No part of India is situated on the equator. Is it possible to have a geostationary satellite which always remains over New Delhi?
17. As the earth rotates about its axis, a person living in his house at the equator goes in a circular orbit of radius equal to the radius of the earth. Why does he/she not feel weightless as a satellite passenger does ?
18. Two satellites going in equatorial plane have almost same radii. As seen from the earth one move from east to west and the other from west to east. Will they have the same time period as seen from the earth? If not, which one will have less time period ?
19. A spacecraft consumes more fuel in going from the earth to the moon than it takes from a retun trip. Comment on this statement.
1. The acceleration of moon with respect to earth is 0.0027 m/s2 and the acceleration of an apple falling on earth’s surface is about 10 m/s2. Assume that the radius of the moon is one fourth of the earth’s radius. If the moon is stopped for an instant and then released, it will fall towards the earth. The initial acceleration of the moon towards the earth will be.
(A) 10 m/s2 (B*) 0.0027 m/s2 (C) 6.4 m/s2 (D) 5.0 m/s2
2. The acceleration of the moon just before it strikes the earth in the previous question is
(A) 10 m/s2 (B) 0.0027 m/s2 (C*) 6.4 m/s2 (D) 5.0 m/s2
3. Suppose, the acceleration due to gravity at the earth’s surface is 10 m/s2 and at the surface of Mars it is 4.0 m/s2. A 60 kg passenger goes from the earth to the Mars in a spaceship moving with a constant velocity. Neglect all other object in the sky. Which part of fig. best represents the weight (net gravitational force) of the passenger as a function of time.
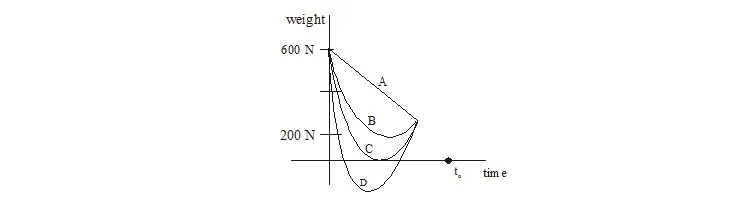
(A) A (B) B (C*) C (D) D
4. Consider a planent in some solar system which has a mass double the mass of the earth and density equal to the average density of the earth. An object weighing W on the earth will weigh
(A) W (B) 2 W (C) W / 2 (D*) 2 1/3 W at the planet
5. If the acceleration due to gravity at the surface of the earth is g, the work done in slowly lifting a body of mass m from the earth’s surface to a height R (equal to the radius of the earth) is
(A*) 1/2 mgR (B) 2 mgR (C) mgR (D) 1/4 mgR
6. A person brings a mass of 1 kg from infinity to a point A. Initially the mass was at rest but it moves at a speed of 2 m/s as it reaches A. The work done by the person on the mass is -3 J. The potential at A is
(A) –3 J/kg (B) –2 J/kg (C*) –5 j/kg (D) none of these
7. Let V and E be the gravitational potential and gravitational field at a distance r from the centre of uniform spherical shell, Consider the following two statements:
(a) The plot of V against r is discontinuous
(b) The plot of E against r is discontinuous
(A) Both A and B are correct (B) A is correct but B is wrong
(C*) B is correct but A is wrong (D) Both A and B are wrong
8. Let V and E represent the gravitational potential and field at a distance r from the centre of uniform solid sphere, Consider the two statements:
(a) The plot of V against r is discontinuous
(b) The plot of E against r is discontinuous
(A) Both A and B are correct (B) A is correct but B is wrong
(C) B is correct but A is wrong (D*) Both A and B are wrong
9. Take the effect of bulging at equator of the earth and its rotation in account. Consider the following statements:
HCV_Ch-11_obj I _9
(A) There are points outside the earth where the value of g is equal to its value at the equator.
(B) There are points outside the earth where the value of g is equal to its value at the poles.
(A) Both A and B are correct (B*) A is correct but B is wrong.
(C) B is correct but A is wrong. (D) Both A and B are wrong
10. The time period of an earth-satellite in circular orbit is independent of
HCV I _Ch-11_Obj.1_10
(A*) the mass of the satellite (B) radius of the orbit
(C) none of them (D) both of them
11. The magnitude of gravitational potential energy of the moon-earth system is U with zero potential energy at infinite separation. The kinetic energy of the moon with respect to the earth is K.
(A) U < K (B*) U > K (C) U = K
12. Fig. shows the elliptical path of a planet about the sun. The two shaded parts have equal area. If t1 and t2 be the time taken by the planet to go from a to b and from c to d respectively
(A) t1 < t2 (B*) t1 = t2 (C) t1 > t2
(D) insufficient information to deduce the relation between t1 and t2.
13. A person sitting in a chair in a satellite feels weightlessness because
HCV_Ch-11_obj I _13
(A) the earth does not attract the objects in a satellite
(B) the normal force by the chair on the person balances the earth’s attraction
(C*) the normal force is zero
(D) the person in satellite is not accelerated
14. A body is suspended from a spring balance kept in a satellite. The reading of the balance is W1 when the satellite goes in a an orbit of radius R and is W2 when it goes in an orbit or radius 2 R.
HCV_Ch-11_Obj.1_14
(A*) W1 = W2 (B) W1 < W2 (C) W1 > W2 (D) W1 ¹ W2
15. The kinetic energy needed to project a body of mass m from the earth’s surface to infinity is
(A) 1/4 mgR (B) 1/2 mgR (C*) mgR (D) 2 mgR
16. A particle is kept at rest at a distance R (earth’s radius) above the earth’s surface. The minimum speed with which it should be projected so that it does not return is 
1. Let V and E denote the gravitational potential and gravitational field at a point. It is possible to have
(A*)V = 0 and E = 0 (B*)V = 0 and E ¹ 0 (C*) V ¹ 0 and E = 0 (D*) V ¹ 0 and E ¹ 0
2. Inside a uniform spherical shell
(A) the gravitational potential is zero
(B*) the gravitational field is zero
(C*) the gravitational potential is same everywhere
(D*) the gravitational field is same everywhere
3. A uniform spherical shell gradually shrinks maintaining its shape. The gravitational potential at the centre HCV_Ch-11_Obj.II_3
(A) increase (B*) decreases (C) remains constant (D) oscillates
4. Consider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sum
(A) is zero in any small part of the orbit (B*) is zero in some parts of the orbit
(C*) is zero in one complete revolution (D) is zero in no part of the motion
5. Two satellites A and B move round the earth in the some orbit. The mass of B is twice the same of A.
HCV_11_Obj II_5
(A*) Speeds of A and B are equal
(B) the potential energy of earth + A is same as that of earth + B.
(C) The kinetic energy of A and B are equal
(D) The total energy of earth + A is same as that of earth + B
6. Which of the following quantities remain constant in a planetary motion (consider elliptical orbits) as seen from the sun?
(A) speed (B) Angular speed (C) Kinetic energy (D*) Angular momentum
1. Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.
Sol1. 6.67 × 10–7 N
2. Four particles having masses m, 2m, 3m and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
Sol 2. {4(1.414)Gm2 }/ a2
3. Three equal masses m are placed at the three corners of an equilateral triangle of side a. Find the force exerted by this system on another particle of mass m placed at (a) the mid-point of a side, (b) at the centre ofthe triangle.
Sol 3. (a)4Gm2/3a2 , (b) zero
4. Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two. 
6. Find the acceleration due to gravity of the moon at a point 1000 km above the moon’s surface. The mass of the moon is 7.4 × 1022 kg and its rdius is 1740 km.
Sol 6. 0.65 m/s2
7. Two small bodies of masses 10 kg and 20 kg are kept distance 1.0 m apart and released. Assuming that only mutual gravitational froces are acting, find the speeds of the particles when the separation decrease to 0.5 m.
Sol 7. 4.2 × 10–5 m/s and 2.1 × 10–5 m/s
8. A semicircular wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. Find the gravitational attraction on the particle due to the wire.
Sol 8. 2(3.14)GMm/L2
9. Derive an expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the centre.
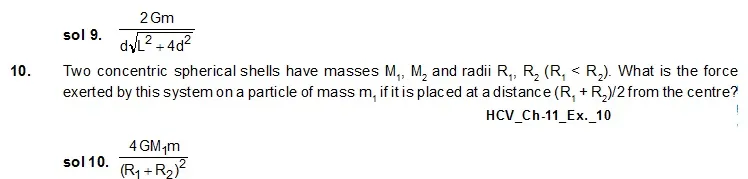
11. A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
Sol 11. GMemx/R3
12. A tunnel is dug along a chord of the earth at a perpendicular distance R/2 from the earth’s centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mas m when it is at a distance x from the centre of the tunnel.
Sol 12.GMem/2R2

15. A thin spherical shell having uniform density is cut in two parts by a plane and kept separated as shown in figure. The point A is the centre of the plane section of the first part and B is the centre of the plane section of the second part. Show that the gravitational feld at A due to the first part is equal in
magnitude ot the gravitational field at B due to the second part.

16. Two small bodies of masses 2.00 kg and 4.00 kg are kept at rest at a separation of 2.0 m. Where should a particle of mass 0.10 kg be placed to experience no net gravitational force from these bodies? The particle is placed at this point. What is the gravitational potential energy of the system of three particles with usual reference level ?
16.0.83 m from the 2.00 kg body towards the other body, – 3.06× 10–10 J
17. Three particles of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
Sol 17. 3Gm2/2a
18. A particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
18. 6.67 × 10–10 J

22. Find the height over the earth’s surface at which the weight of a body becomes half of its value at the surface.
22. (1.414 – 1) times the radius of the earth
23. What is the acceleration due to gravity on the top of Mount Everest ? Mount Everst is the height mountain peak of the world at the height of 8848 m. The value at sea level is 9.80 m/s2.
23. 9.77 m/s2
24. Find the acceleration due to the gravity in a mine of depth 640 m if the value at the surface is 9.800 m/s2. The radius of the earth is 6400 km.
24. 9.799 m/s2
25. A body is weighed by a spring balance to be 1.000 kg at the north pole. How much will it weigh at the equator? Account for the earth’s rotation only.
25. 0.997 kg
26. A body stretches a spring by a particular length at the earth’s surface at equator. At what height above the south pole will it stretch the same spring by the same length ? Assume the earth to be spherical.
26. 10 km approx
27. At what rate should the earth rotate so that the apparent g at the equator becomes zero ? What will be the length of the day in this situation?
27. 1.237 × 10–3 rad/sec, 1.41 h

29. The time taken by Mars to revolve round the sun is 1.88 years. Find the ratio of average distance between Mars and thesun to that between the earth and the sun.
29. 1.52
30. The moon takes about 27.3 days to revolve round the earth in a nearly circular orbit of radius 3.84 × 105 km. Calculate the mass of the earth from these data.
30. 6.02 × 1024 kg
31. A Mars satellite moving in an orbit of radius 9.4 × 103 km takes 27540 s to complete one revolution. Calculate the mass of Mars.
31. 6.5 × 1023 kg
32. A satelite of mass 1000 kg is supposed to orbit the earth at a height of 2000 km above the earth’s surface. Find (a) its speed in the orbit, (b) its kinetic energy, (c) the potential energy of the earth-satellite system and (d) its time period. Mass of the earth = 6 × 1024 kg.
32. (a) 6.90 km/s (b) 2.38 × 1010 J (c) – 4.76 × 1010 J with usual reference (d) 2.01 hours
33. (a) Find the radius of the circular orbit of a satellite moving with an angular speed equal to the angular speed of earth’s rotation. (b) If the satellite is directly above the north pole at some instant, find the time it takes to come over the equatorial plane. Mass of the earth = 6 × 1024 kg.
33. (a) 42300 km (b) 6 hours
34. What is the true weight of an object in a geostationary satellite that weighed excatly 10.0 N at the north pole?
34. 0.23 N
35. The radius of a planet is R1 and a satellite revolves round it in a circle of radius R2. The time periof of revolution is T. Find the acceleration due to the gravitation of the planet at its surface.

36. Find the minimum colatitude which can directly receive a signal from a geostationary satellite.
36. sin–1 (0.15)
37. A particle is fired vertically upward from earth’s surface and it goes upto a maximum height of 6400 km. Find the initial speed of the particle.
37. 7.9 km/s
38. A particle is fired vertically upward with a speed of 15 km/s. With what speed will it move in intersteller space. Assume only earth’s gravitational field.
38. 10.0 km/s
39. A mass of 6 × 1024 kg (equal to the mass of the earth) is to be compressed in a sphere in such a way that the escape velocity from its surface is 3 × 108 m/s. What should be the radius of the sphere?
39. » 9 mm