GEOMETRY & MENSURATION
Basic Conversions

Straight Lines
Parallel Lines: Two straight lines are parallel if they lie on the same plane and do not intersect however far produced.
Transversal : It is a straight line that intersects two parallel lines. When a transversal intersects two parallel lines then
1. Corresponding angles are equal, (that is: For the figure below)
1 = 5; 2 = 6; 4 = 8; 3 = 7
2. Alternate interior angles are equal, that is (Refer figure below.)
4 = 6; 5 = 3
3. Alternate exterior angles are equal, that is
2 = 8; 1 = 7
4. Interior angles on the same side of transversal add up to 180°, that is
4 + 5 - 3 + 6 = 180°
Polygons
Polygons are plane figures formed by a closed series of rectilinear (straight) segments. Example: Triangle, Rectangle...
Polygons can broadly be divided into two types:
(a) Regular polygons: Polygons with all the sides and angles equal.
(b ) Irregular polygons: Polygons in which all the sides or angles are not of the same measure.
Polygon can also be divided as concave or convex polygons.
Convex polygons are the polygons in which all the diagonals lie inside the figure otherwise it's a concave polygon
Polygons can also be divided on the basis of the number of sides they have.
No. of sides Name of Sum of all
the polygon the angles
1 Triangle 180°
2 Quadrilateral 360°
3 Pentagon 540°
4 Hexagon 720°
5 Heptagon 500°
6 Octagon 1080°
7 Nonagon 1260°
8 Decagon 1440°
Properties
1. Sum of all the angles of a polygon with n sides = (2n – 4) p/2 or (n – 2)p Radians = (n – 2) 180° degrees
2. Sum of all exterior angles = 360° i.e. In the figure below:
q1 + q2 + ....+q6 = 360°
In general, q1 + q2 + ....+qn = 360°
3. No. of sides = 360q1 + q2 + ....+q6 = 360°/exterior angles.
4. Area = (ns2/4) × cot (180/n); where s = length of side, n = no. of sides.
5. Perimeter = n × s.
Triangles (D)
A triangle is a polygon having three sides. Sum of all the angles of a triangle = 180°
Types 1. Acute angle triangle: Triangles with all three angles acute (less than 90°).
2. Obtuse angle triangle: Triangles with one of the angles obtuse (more than 90°).
Note: We cannot have more than one obtuse angle in a triangle.
3. Right angle triangle: Triangle with one of the angles equal to 90°.
4. Equilateral triangle: Triangle with all sides equal. All the angles in such a triangle measure 60°.
5. isosceles triangle: Triangle with two of its sides equal and consequently the angles opposite the equal sides are also equal.
6. Scalene Triangle: triangle with none of the sides equal to any other side.
Properties (General)
Sum of the length of any two sides of a triangle has to be always greater than the third side.
Difference between the lengths of any two sides of a triangle has to be always lesser than the third side.
Side opposite to the greatest angle will be the greatest and the side opposite to the smallest angle the smallest.


Area
1. Area = 1/2 base × height or 1/2 bh.
Height = Perpendicular distance between the base and vertex opposite to it
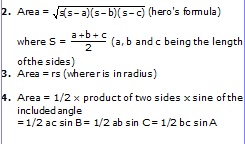
4. Area = abc/4R
Where R = circum radius
Congruency of Triangles
Two triangles are congruent if all the sides of one are equal to the cooresponding sides of another.
It follows that all the angles of one are equal to the corresponding angles of another. The notation for congruency is .
Conditions for Congruency
1. SAS congruency: If two sides and an included angle of one triangle are equal to two sides and an included angle of another,
the two triangles are congruent. (See figure below.)
![]()

2. ASA congruency: If two angles and the included side of one triangle is equal to two angles and the
included side of another, the triangles are congruent. (See figure below)
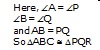
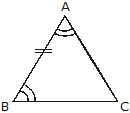
3. AAS congruency: If two angles and side opposite to one of the angles is equal to the corresponding
angles and the side of another triangle, the triangles are congruent. In the figure below:
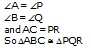

4. SSS congruency: If three sides of one triangle are equal to three sides of another triangle, the two triangles are congruent. In the figure below:
![]()
5. SSA congruency: If two sides and the angle opposite the greater side of one triangle are equal to the two sides and the angle opposite
to the greater side of another triangle, then the triangles are congruent. The congruency doesn't hold if the equal angles lie opposite the shorter side. In the figure below, if
![]()
Then the triangles are congruent.
i.e. DABC DPQR.
Similarity of Triangles Similarity of triangles is a special case where if either of the
conditions of similarity of polygons holds the other will hold automatically.
Types of similarity
1. AAA similarity: If in two triangles, corresponding angles are equal, that is, the two triangles are equiangular then the triangles are similar.
Corollary (AA similarity): If two angles of one triangle are respectively equal to two angles of another triangle
then the two triangles are similar. The reason being, the third angle becomes equal automatically.
2. SSS similarity: If the corresponding sides of two triangles are proportional then they are similar.
For DABC to be similar to DPQR, AB/PQ = BC/QR = AC/PR, must hold true.
3. SAS similarity: If in two triangles, one pair of corresponding sides are proportional and the included angles are equal then the two triangles are similar.
DABC ~ DPQR
If AB/BC = PQ/QR and ÐB = ÐQ
Note: In similar triangles; the following identity holds:
Ratio of medians = Ratio of heights = Ratio of circummradii = Ratio of inradii = Ratio of angle bisectors
While there are a lot of methods through which we see similarity of triangles, the one thing that all our Maths teachers forgot to
tell us about similarity is the basic real life concept of similarity i.e. Two thigs are similar if they look similar !!
If you have been to a toy shop lately, you would have come across models of cars or bikes which are made so that they look like
the original - but are made in a different side from the original. Thus you might have seen a toy Maruti car which is built in a ratio of 1:25
of the original car. The result of this is that the toy car would look very much like the original car (of course if it is built well!!). Thus if you
have ever seen a father and son looking exactly like each other, you have experienced similarity!!
You should use this principle to identify similar triangles. In a figure two triangles would be similar simply if they look like one another.
Thus, in the figure below if you were to draw the radii OB and O'A the two triangles MOB and MO'S will be similar to each other. Simply
because they look similar. Of course, the option of using the different rules of similarity of triangles still remains with you.
Equilateral Triangles (of side a):
1.
![]()

Properties
1. The incentre and circumcentre lies at a point that divides the height in the ratio 2 : 1.
2. The circum radius is always twice the in radius.
[R = 2r].
3. Among all the triangles that can be formed with a given perimeter, the equilateral triangle will have te maximum area.
4. An equilateral triangle in a circle will have the maximum area compared to other triangles inside the same circle.
Isosceles Triangles
![]()
In an isosceles triangle, the angles opposite to the equal sides are equal.
Right Angled Triangle
Pythagoras Theorem In the case of a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In the figure below, for triangle ABC,
a2 = b2 + c2
Area = 1/2 (product of perpendicular sides)
R(circumradius) =
Area = rs
(where r = in radius and s = (a + b + c)/2 where a, b and c are sides of the triangle)
Þ 1/2 bc = r(a + b + c)/2
Þ r = (bc)/(a + b + c)

These triplets are very important since a lot of questions are based on them.
Any triplet formed by either multiplying or dividing one of the basic triplets by any positive real number will be anotehr Pythagorean triplet.
Thus, since 3,4,5 form a triplet so also will 6,8 and 10 as also 3.3, 4.4 and 5.5.
Similarity of Right Triangles Two right triangles are similar if the hypotenuse and side of one is proportional to hypotenuse
and side of anoter. (RHS - similarity - Right angles hypotenuse side).
Important Terms with Respect to a Triangle
1. Median A line joining the mid-point of a side of a triangle to the opposite vertex is called a median. In the figure the
three medians are PG,Qf and RE where G,E and F are mid-points of their respective sides.
A median divides a triangle into two parts of equal area.
The point where the three medians of a triangle meet is called the centroid of the triangle.
The centroid of a triangle divides each median in the ratio 2 : 1.
i.e. PC : CG = 2 : 1 = QC : CF = RC : CE
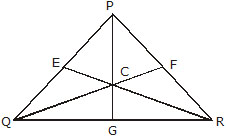
Important formula with respect to a median
![]()
2. Altitude/Height A perpendicular drawn from any vertex to the opposite side is called the altitude. (In the figure, AD, BF and CE are teh altitude of the triangles).
All the altitudes of a triangle meet at a point called the orthocentre of the triangle.
The angle made by any side at the orthocentre and the vertical angle make a supplementary pair
(i.e. they both add up to 180°). In the figure below.
ÐA + ÐBOC = 180° = ÐC + ÐAOB
3 . Perpendicular Bisectors A line that is a perpendicular to a side and bisects it is the perpendicular bisector of the side.

The point at which the perpendicular bisectors of the sides meet is called the circumcentre of the triangle
The circumcentre is teh centre of the circle that circumscribes the triangle. There can be only one such circle.
Angle formed by any side at the circumcentre is two times the vertical angle opposite to the side. This is the
property of the circle whereby angles formed by an arc at the centre are twice that of the angle formed by the same arc in the opposite arc. Here we can view this as:
ÐQCR = 2 ÐQPR (when we consider arc QR and it's opposite arc QPR)
4. Incentre
The lines bisecting the interior angles of a triangle are the angle bisectors of that triangle.
The angle bisectors meet at a point called the incentre of the triangle.
The incentre is equidistant from all the sides of the triangle.
From the incentre with a perpendicular drawn to any of the sides as the radius, a circle can be drawn touching all
the three sides. This is called the incircle of the triangle. The radius of the incircle is known as inradius.
The angle formed by any side at the incentre is always a right angle more than half the angle opposite to teh side.
This can be illustrated as ÐQIR = 90 + 1/2 ÐP
If QI and RI be the angle bisectors of exterior angles at Q and R then,
QIR = 90 – 12 ÐP.
Quadrilaterals
Area
(A) = 1/2 (product of diagonals) × (sine of the angle between, them)
If q1 and q2 are the two angles made between them selves by the two diagonals, we have by the property of intersecting lines ® q1 + q2 = 180°
Then, the area of the quadrilateral = 1/2 d1 d2 sin q1 = 1/2 d1 d2 sin q2.
(B) Area = 1/2 × diagonal × sum of the perpendiculars to it from opposite vertices
![]()
(C) Area of a circumscribed quadrilateral
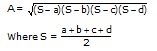
(where a, b, c and d are the lengths of the sides.)
Properties
1. In a covex quadrilateral inscribed in a circle, the product of the diagonals is equal to the sum of the products of the opposite sides. For example, in the figure below:
(a × c) + (b × d) = AC × BD
2. Sum of all the angles of a quadrilateral = 360°.
TYpes of quadrilaterals
1. Parallelogram (|| gm)
A parallelogram is a quadrilateral with opposite sides parallel (as shown in the figure below.)
(A) = Area = Base (b) × Height (h)
= bh
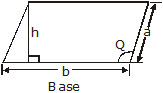
(B) = Area = product of any two adjacent sides × sine of the included angle.
= ab sin Q
(C) Perimeter = 2(a + b)
Where a and b are any two adjacent sides.
Properties
(a) Diagonals of a parallelogram bisect each other.
(b) Bisectors of the angles of a parallelogram form a rectangle.
(c) A parallelogram inscribed in a circle is a rectangle.
(d) A parllelogram circumscribed about a circle is a rhombus.
(e) The opposite angles in a parallelogram are equal.
(f) The sum of the squares of the diagonals is equal to the sum of the squares of the four sides in the figure:
AC2 + BD2 = AB2 + BC2 + CD2 + AD2
= 2(AB2 + BC2)
2. Rectangles
A rectangle is a parallelogram with all angles 90°
(a) Area = Base × Height = b × h
Note: Base and height are also referred to as the length and teh breadth in a rectangle.
![]()
Properties of a Rectangle
(a) Diagonals are equal and bisect each other.
(b) Bisectors of the angles of a rectangle
(a parallelogram) form another rectangle.
(c) All rectangles are parallelograms but the reverse is not true.
3. Rhombus
A parallelogram having all the sides equal is a rhombus.
Properties
(a) Diagonals bisect each other at right angles.
(b) All rhombuses are parallelograms but the reverse is not true.
(c) A rhombus may or may not be a square but all squares are rhombuses.
4. Square
A square is a rectangle with adjacent sides equal or a rhombus with each angle 90°

Properties
(a) Diagonals are equal and bisect each other at right angles.
(b) Side is the diameter of the inscribed circle.
(c) Diagonal is the diameter of the circumscribing circle.
![]()
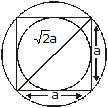
5. Trapezium
A trapezium is a quadrilateral with only two sides parallel to each other.
(a) Area = 1/2 × sum of parallel sides × height = 1/2 (AB + DC) × h – For the figure below.
(b) Median = 1/2 × sum of the parallel sides (median is the line equidistant from the parallel sides)
For any line EF parallel to AB
![]()

Properties
(a) If the non-parallel sides are equal then diagonals will be equal too.
Regular hexagon
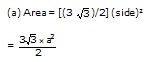
(b) A regular hexagon is actually a combination of 6 equilateral triangles all of side 'a'.
Hence, the area is also given by: 6 × side of
![]()
(c) If you look at the figure closely it will not be difficult to realise that circumradius (R) = a; i.e. the side of the hexagon is equal to the circumradius of the same.
Circles
(a) Area = pr2
(b) Circumference = 2pr = (r = radius)
(c) Area = 1/2 × circumference × r
Arc: It is a part of the circumference of the circle. The bigger one is called the major arc and teh smaller one the minor arc.
(d) Length (Arc XY) = × 2pr
(e) Sector of a circle is a part of the area of a circle between two radii.
(f) Area of a sector = × pr2
(where q is the angle between two radii)
= (1/2)r × length (arc xy)
(\ prq/180 = length arc xy)
= 1/2 × r × 
(g) Segment: A sector minus the triangle formed by the two radii is called the segment of the circle.
(h) Area = Area of the sector – Area DOAB = × pr2 × 1/2 × r2 sin q
(i) Perimeter of segment = length of the arc + length of segment AB

(j) Congruency: Two circles can be congruent if and only if they have equal radii.
Properties
(a) The perpendicular from the centre of a circle to a chord bisects the chord. The converse is also true.
(b) The perpendicular bisectors of two chords of a circle intersect at its centre.
(c) There can be one and only one circle passing through theree or more non-collinear points.
(d) If two circles intersect in two points then the line through the centres is teh perpendicular bisector of the common chord.
(e) If two chords of a circle are equal, then the centre of the circle lies on the angle bisector of the two chords.
(f) Equal chords of a circle or congruent circles are equidistant from the centre.
(g) Equidistant chords from the centre of a circle are equal to each other in terms of their length.
(h) The degree measure of an arc of a circle is twice the angle subtended by it at any point on teh alternate segment of the circle.
This can be clearly seen in the following figure: With respect to the arc AB, ÐAOB = 2 ÐACB.
(i) Any two angles in the same segment are equal. Thus, ÐACB = ÐADB.
(j) The angle subtended by a semi-circle is a right angle. Conversely, the arc of a circle subtending a right angle at any point of the circle in its alternate segment is a semi-circle.
(k) Any angle subtended by a minor arc in the alternate segment is acute, and any angle subtended by a major arc in the alternate segment is obtuse.
In the figure below
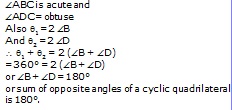
or sum of opposite angles of a cyclic quadrilateral is 180°.
(l) If a line segment joining two points subtends equal angles at two other points lying on the same side of
the line, the four points are concyclic. Thus, in the following figure:
If, q1 = q2
Then ABCD are concyclic, that is, they lie on the same circle.
(m) Equal chords of a circle (or of congruent circles) subtend equal angles at the centre (at the corresponding centres.) The converse is also true.
(n) If the sum of the opposite angles of a quadrilateral is 180°, then the quadrilateral is cyclic.
Secant: A line that intersects a circle at two points.
Tangent: A line that touches a circle at exactly one point.
(o) If a circle touches all the four sides of a quadrilateral then the sum of the two opposite sides is equal to the sum of other two
AB + DC = AD + BC
(p) In two concentric circles, the chord of the larger circle that is tangent to the smaller circle is bisected at the point of contact.
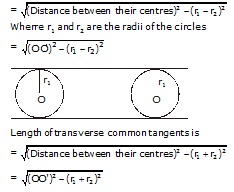
Tangents
Length of direct common tangents is
Ellipse

Part II : mensuration
The following formulae hold true in the area of mensuration:
1. Cubiod
A cuboid is a three dimensional box. It is defined by the virtue of it's length l, breadth b and height h. It can be visualised as a room which has its length, breadth and height different from each other.
1. Total surface area of a cuboid = 2 (lb + hb + lh)
2. Volume of the cuboid = lbh
2. Cube of side s
A cube is a cuboid which hgas all its edges equal i.e. length = breadth = height = s.
1. Total surface area of a cube = 6s2.
2. volume of the cube = s3.
3. Prism
A prism is a solid which can have any polygon at both its ends. It's dimensions are defined by the dimensions of the polygon at it's ends and its height.
Ex. 1 A right triangle with hypotenuse 10 inches and other two sides of variable length is rotated about its longest side thus giving rise to a solid. Find the maximum possible area of such a solid.
(A) (250/3)pin2 (B) (160/3)pin2 (C) 325/3)pin2 (D) None of these
Sol. Most of the questions like this that are asked in the CAT will not have figures accompanying them. Drawing a figure takes time so it is always
better to strengthen our imagination. The beginners can start off by trying to imagine the figure first and trying to solve the problem. They can draw the
figure only when they don't arrive at the right answer and then find out where exactly they went wrong. The key is to spend as much time with the problem as possible trying to
understand it fully and analysing the different aspects of the same without investing too much time on it.
Let's now look into this problem. The key here lies in how quickly you are able to visualise the figure and are able to see that
(i) the triangle has to be an isosceles triangle,
(ii) the solid thus formed is actually a combination of two cones,
(iii) the radius of the base has to be the altitude of the triangle to the hypotenuse.
After you have visualised this comes the calculation aspect of the problem. This is one aspect where you can score over others.
Ex.2 A right circular cylinder is to be mae out of a metal sheet such that the sum of its height and radius does not exceed 9 cm can have an area of maximum.
(A) 54 p cm2 (B) 108 p cm2 (C) 81 p cm2 (D) None of these
Sol. Solving this question requires the knowledge of ratio and proportion also. To solve this question, one must know that for a2b3c4 to have
the maximum value when (a + b + c) is constant a, b and c must be in the ratio 1 : 2 : 3. Now lets look at this problem. Volume of a cylinder = pr2h.
If you analyse this formula closely, you will find that r and h are the only variable term. So for volume of the cylinder to be maximum,
r2h has to be maximum under the condition that r + h = 9. By the information given above, this is possible only when r : h = 2: 1, that is, r = 6, h = 3 So,
Volume of the cone = pr2h
= p × 62 × 3
108p
Ex.3 A chord AB of a circle of radius 5.25 cm makes an angle of 60° at the centre of the circle. Find teh area of the major and minor segments. (Take p = 3.14)
(A) 168 cm2 (B) 42 cm2 (C) 84 cm2 (D) None of these
Sol. The moment you finish reading this question, it should occur to you that this has to be an equilateral triangle. Once you realise this, the question is reduced to just calculations.
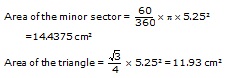
Area of the minor segment = Area of the minor sector
– Area of the triangle = 2.5 cm2
Area of the major segment = Area of the circle – Area of the minor segment.
= 86.54 cm2 – 2.5 cm2 = 84 cm2
ASSIGNMENT
1. A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts the shadow 50 m long on the ground. Find the height of the tower.
(A) 100 m (B) 120 m
(C) 25 m (D) 200 m
(E) 225 m
2. In the figure, DABC is similar to DEDC.

If we have AB = 4 cm,
ED = 3 cm, CE = 4.2 and
CD = 4.8 cm, find the value of CA and CB
(A) 6 cm, 6.4 cm (B) 4.8 cm, 6.4 cm (C) 5.4 cm, 6.4 cm (D) 5.6 cm, 6.4 cm
(E) 5.4 cm, 6.0 cm
3. The area of similar triangles, ABC and DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger DABC be 36 cm, then the longest side of smaller DDEF is
(A) 20 cm (B) 26 cm
(C) 27 cm (D) 30 cm
(E) 36 cm
4. Two isosceles Ds have equal angles and their areas are in the ratio 16:25. Find the ratio of their corresponding heights.
(A) 4/5 (B) 5/4
(C) 3/2 (D) 5/7
(E) None of these
5. The area of two similar Ds are respectively 9 cm2 and 16 cm2. Find the ratio of their corresponding sides.
(A) 3 : 4 (B) 4 : 3
(C) 2 : 3 (D) 4 : 5
(E) 5 : 4
6. In the given figure find ÐADB.
(A) 132° (B) 144°
(C) 48° (D) 96°
(E) None of these
7. In the given two straight line, PQ and RS intersect each other at O. If ÐSOT = 75°, find the value of a,b and c.
(A) a = 84°, b = 21°, c = 48°
(B) a = 48°, b = 20°, c = 50°
(C) a = 72°, b = 24°, c = 54°
(D) a = 64°, b = 28°, c = 45°
(E) a = 68°, b = 20°, c = 45°
8. In the following figure, find the value of x
(A) 40°
(B) 25°
(C) 30°
(D) 45°
(E) 50°
9. In the figure, AB is parallel to CD and RD || SL || TM || AN, and BR : RS : ST : TA = 3 : 5 : 2 : 7. If it is known that CN = 1.333 BR. Find the ratio of BF : FG : GH : HI : IC
(A) 3 : 7 : 2 : 5 : 4 (B) 3 : 5 : 2 : 7 : 4 (C) 4 : 7 : 2 : 5 : 3 (D) 4 : 5 : 2 : 7 : 3
(E) None of these
10. In a right angled triangle, find the hypotenuse if base and perpendicular are respectively 36015 cm and 48020 cm.
(A) 69125 cm (B) 60025 cm (C) 391025 cm (D) 60125 cm
11. The perimeter of an equilateral triangle is cm. Find its height.
(A) 63 metres (B) 24 metres (C) 18 metres (D) 36 metres
(E) 32 metres
12. The inner circumference of a circular track is 440 cm. The track is 14 cm wide. Find the diameter of the outer circle of the track.
(A) 84 cm (B) 168 cm
(C) 336 cm (D) 77 cm
(E) 80 cm
13. A race track is in the form of a ring whose inner and outer circumference are 352 metre and 396 metre respectively. Find the width of the track.
(A) 7 metres (B) 14 metres (C) 14p metres (D) 7p metres
(E) None of these
14. The outer circumference of a circular track is 220 metre. The tracks is 7 metre wide everywhere.
Calculate the cost of levelling the track at the rate of 50 paise per square metre.
(A) Rs. 1556.5 (B) Rs. 3113
(C) Rs. 593 (D) Rs. 1386
(E) Rs. 693
15. The areas of three adjacent faces of a cuboid are x, y, z. If the volume is V, then V2 will be equal to
![]()
16. In the adjacent figure, find the area of the shaded region. (Use = 22/7)
(A) 15.28 cm2 (B) 6.14 cm2
(C) 30.57 cm2 (D) 40.76 cm2
(E) None of these
17. The diagram represents the area swept by the wiper of a car. With the dimensions given in
the figure, calculate teh shaded area swept by the wiper.
(A) 102.67 cm (B) 205.34 cm (C) 51.33 cm (D) 208.16 cm
(E) Cannot be determined
18. Find the area of the quadrilateral ABCd.![]()
(A) 452 sq units
(B) 269 sq units
(C) 134.5 sq units
(D) 1445 g cm
(E) Cannot be determined
19. The base of a pyramid is a rectangle of sides 18 m × 26 m and its slant height to the shorter side of the base is 24 m. Find its volume.

20. A wire is looped in the form of a circle of radius 28 cm. It is bent again into a square form. What will be the length of the diagonal of the largest square possible thus ?
21. The sides of a triangle are 21, 20 and 13 cm. Find the area of the larger triangle into
which the given triangle is divided by the perpendicular upon the longest side from the opposite vertex.
(A) 72 cm2 (B) 96 cm2
(C) 168 cm2 (D) 144 cm2
(E) 150 cm2
22. A circular tent is cylindrical to a height of 3 metres and conical above it. If its diameter is 105 m and the slant
height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
(A) 3894 (B) 973.5
(C) 1947 m (D) 1800 m
(E) None of these
23. A solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 19 cm and the diameter
of the cylinder is 7 cm. Find the total surface area of the solid. (Use = 22/7).
(A) 398.75 cm2
(B) 418 cm2
(C) 444 cm2
(D) 412 cm2
(E) 500 cm2
24. A cone, a hemisphere and a cylinder stand on equal bases and have the same height. What is the ratio of their volumes ?
(A) 2 : 1 : 3 (B) 25 : 1 : 3 (C) 1 : 2 : 3 (D) 1.5 : 2 : 3
(E) 2 : 3 : 1
25. Find the sum of the areas of the shaded sectors given that ABCDFE is any hexagon and all the circles are of same
radius r with different vertices of the hexagon as their centres as shown in the figure.
![]()
1) A 2) D 3) C 4) A 5) A 6) A 7) A 8) A 9) B 10) B 11) D 12) B 13) A 14) E 15) E 16) C
17) A 18) B 19) A 20) B 21) B 22) C 23) B 24) C 25) B