RATIO AND PROPORTION
Mathematical numbers used in comparing two things which are similar to each other in terms of units are ratios.
A ratio can be written in three different ways viz, x to y, x: y and
x/y
but read as the ratio of x to y.
For example:
The ratio of 4 to 5 is 4: 5.
Ram’s weight is 40 kgs and Ali’s weight is 80 kgs. To find out the ratio of Ram’s weight to Ali’s weight we need to divide
Ram’s weight to Ali’s weight. Therefore, the ratio between Ram’s and Ali’s weight is
40/80
= 1:2
Comparing things similar to each other is the concept of ratio. And when two ratios are the same, they are said to be in
proportion to each other. It is represented by the symbol ‘::’ or ‘=’.
Golden ratio
Two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to larger of the two quantities.
If two numbers a and b are in golden ratio, then
![]()
It is approximately equal to 1.618.
Ratio
• The ratio is the comparison of a quantity with respect to another quantity.
• It is denoted by “:“.
• Two quantities can be compared only if they are in the same unit.
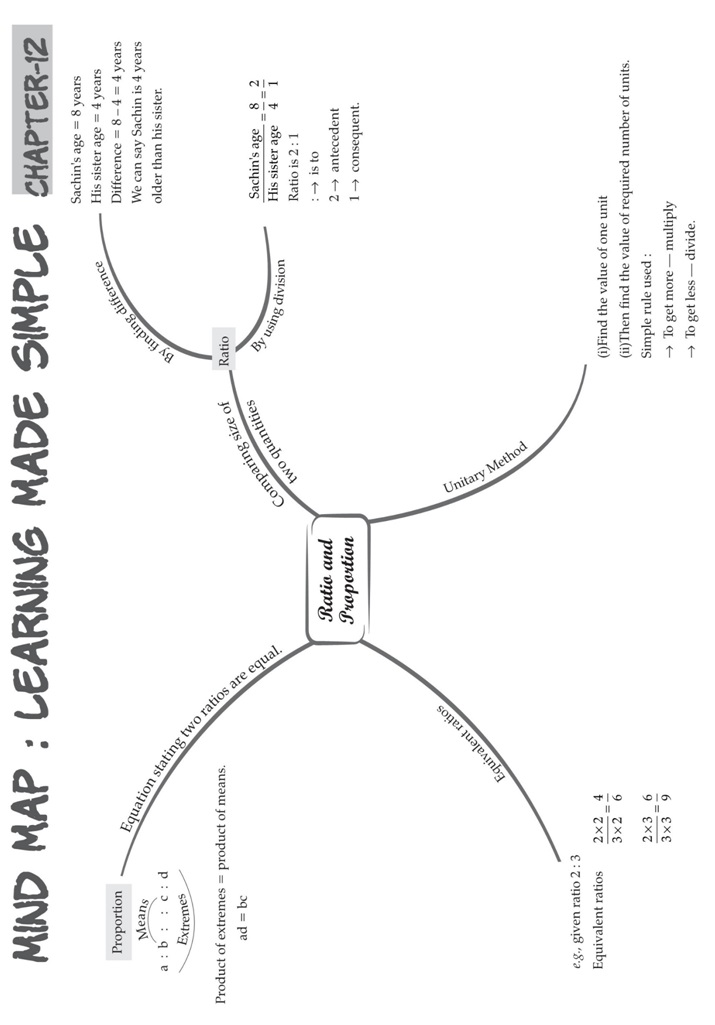
Example: Father’s age is 75 years and the daughter’s age is 25 years.
⇒The ratio of father’s age to daughter’s age
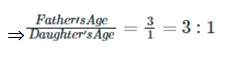
Difference between fractions and ratios
• A fraction describes a part of a whole and its denominator represents the total number of parts.
• Example: 13 means one part out of 3 parts.
• A ratio is a comparison of two different quantities.
• Example: In a society, 10 people like driving, 20 people like swimming and the total
number of people in society is 30.
• The ratio of the number of people liking driving to the total number of people = 10:30.
• The ratio of the number of people liking swimming to the number of people liking driving is 20:10.
Same ratio in different situations
Ratios can remain same in different situations.
Example:
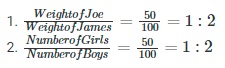
Here, both the above ratios are equal.
Comparing quantities using ratios
Quantities can be compared using ratios.
Example: Joe worked for 8 hours and James worked for 2 hours. How many times Joe’s working hours
is of James’ working hours?
Solution: Working hours of Joe = 8 hours
⇒Working hours of Sheela = 2 hours
⇒The ratio of working hours of Joe to Sheela = 8/2=4
Therefore, Joe works four times more than James.
To know more about Comparison of Ratios,
Comparison of Ratios
Let us consider a problem statement to understand the concept of comparison of ratios.
Statement: An architect states that the buildings that have the ratio of span to height more than
1:4 is only feasible. The dimensions of the plans of various buildings are laid before him.
See the table below.
Read: Ratio and Proportion
Let us find out the span to height ratios for all the buildings in the simplest form.

Building A = 3/5
Building B = 1/5
Building C = 1/3
Compare this with the ratio given by the architect.
For Building A,

The question mark above can be anything, >, < or =.
Cross multiplying the terms,
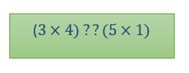
We get,
12 > 5
Hence we can say ratio ¾ is greater than¼. According to the problem statement, this satisfies the
criteria as per the architect. Therefore Building A is feasible.
Similarly calculating for other buildings, for Building B, we find that 1/5 is less than ¼ and for Building
C, 1/3 is greater than ¼. Hence Buildings A and C are feasible while building B is not feasible.
Concept of comparison of ratios is used for the design of aeroplanes to tall buildings to large ships.
Equivalent Ratios
When the given ratios are equal, then these ratios are called as equivalent ratios.
Equivalent ratios can be obtained by multiplying and dividing the numerator and denominator
with the same number.
Example: Ratios 10:30 (=1:3) and 11:33 (=1:3) are equivalent ratios.
Unitary Method
The method in which first we find the value of one unit and then the value of required number of units is
known as Unitary Method.
Example: Cost of two shirts in a shop is Rs.200. What will be the cost of 5 shirts in the shop?
Solution: Cost of 2 shirts = Rs.200
⇒Cost of 1 shirt = 200/2=100
⇒Cost of 5 shirts = (200/2)×5=100×5
= Rs. 500
Proportions
If two ratios are equal, then they are said to be in proportion.
Symbol “::” or “=” is used to equate the two ratios.
Example: Ratios 2:3 and 6:9 are proportional.
⇒ 2:3 :: 6:9 or 2:3 = 6:9
The unitary method is a method in which you find the value of a unit and then the value of a required
number of units. What can units and values be?
Suppose you go to the market to purchase 6 apples. The shopkeeper tells you that he is selling 10 apples for Rs 100.
In this case, the apples are the units, and the cost of the apples is the value. While solving a problem using the unitary
method, it is important to recognize the units and values.
For simplification, always write the things to be calculated on the right-hand side and things known on the left-hand side.
In the above problem, we know the amount of the number of apples and the value of the apples is unknown. It should be
noted that the concept of ratio and proportion is used for problems related to this method.
Example of Unitary Method
Consider another example; a car runs 150 km on 15 litres of fuel, how many kilometres will it run on 10 litres of fuel?
In the above question, try and identify units (known) and values (unknown).
Kilometre = Unknown (Right Hand Side)
No of litres of fuel = Known (Left Hand Side)
Now we will try and solve this problem.
15 litres = 150 km
1 litre = 150/15 = 10 km
10 litres = 10 x 10 = 100 km
The car will run 100 kilometres on 10 litres of fuel.
Unitary Method in Ratio and Proportion
If we need to find the ratio of one quantity with respect to another quantity, then we need to use the
unitary method. Let us understand with the help of examples.
Example: Income of Amir is Rs 12000 per month, and that of Amit is Rs 191520 per annum. If the monthly
expenditure of each of them is Rs 9960 per month, find the ratio of their savings.
Solution: Savings of Amir per month = Rs (12000 – 9960) = Rs 2040
In 12 month Amit earn = Rs.191520
Income of Amit per month = Rs 191520/12 = Rs. 15960
Savings of Amit per month = Rs (15960 – 9960) = Rs 6000
Therefore, the ratio of savings of Amir and Amit = 2040:6000 = 17:50
Types of Unitary Method
In the unitary method, the value of a unit quantity is calculated first to calculate the value of other units.
It has two types of variations.
Direct Variation
Inverse Variation
Direct Variation
In direct variation, increase or decrease in one quantity will cause an increase or decrease in another quantity.
For instance, an increase in the number of goods will cost more price.
Also, the amount of work done by a single man will be less than the amount of work done by a group of men.
Hence, if we increase the number of men, the work will increase.
Indirect Variation
It is the inverse of direct variation. If we increase a quantity, then the value of another quantity gets decrease.
For example, if we increase the speed, then we can cover the distance in less time. So, with an increase in speed,
the travelling time will decrease.
Applications of Unitary Method
The unitary method finds its practical application everywhere ranging from problems of speed, distance,
time to the problems related to calculating the cost of materials.
The method is used for evaluating the price of a good.
It is used to find the time taken by a vehicle or a person to cover some distance in an hour.
It is used in business to determine profit and loss.
Uses of ratios and proportions
Example: Suppose a man travelled 80 km in 2 hours, how much time will he take to travel 40 km?
Solution: If x is the required time, then the proportion is
80:2::40:x.
80/2×40/x
80x = 80
X = 1 hour
So, the man takes one hour to complete 40 km.
Ratio and Proportion in Maths
The definition of ratio and proportion is described here in this section. Both concepts are an important part of
Mathematics. In real life also, you may find a lot of examples such as the rate of speed (distance/time) or price
(rupees/meter) of a material, etc, where the concept of the ratio is highlighted.
Proportion is an equation that defines that the two given ratios are equivalent to each other. For example, the
time taken by train to cover 100km per hour is equal to the time taken by it to cover the distance of 500km
for 5 hours. Such as 100km/hr = 500km/5hrs.
Ratio Meaning
In certain situations, the comparison of two quantities by the method of division is very efficient. We can say
that the comparison or simplified form of two quantities of the same kind is referred to as a ratio. This relation
gives us how many times one quantity is equal to the other quantity. In simple words, the ratio is the number
that can be used to express one quantity as a fraction of the other ones.
The two numbers in a ratio can only be compared when they have the same unit. We make use of ratios to
compare two things. The sign used to denote a ratio is ‘:’.
A ratio can be written as a fraction, say 2/5. We happen to see various comparisons or say ratios in our daily life.
Hence, the ratio can be represented in three different forms, such as:
Proportion
Proportion is an equation that defines that the two given ratios are equivalent to each other. In other words,
the proportion states the equality of the two fractions or the ratios. In proportion, if two sets of given numbers
are increasing or decreasing in the same ratio, then the ratios are said to be directly proportional to each other.
For example, the time taken by train to cover 100km per hour is equal to the time taken by it to cover the
distance of 500km for 5 hours. Such as 100km/hr = 500km/5hrs.
Ratio and proportions are said to be faces of the same coin. When two ratios are equal in value, then they are
said to be in proportion. In simple words, it compares two ratios. Proportions are denoted by the
symbol ‘::’ or ‘=’.
The proportion can be classified into the following categories, such as:
Direct Proportion
Inverse Proportion
Continued Proportion
Direct Proportion
The direct proportion describes the relationship between two quantities, in which the increases in one quantity, there
is an increase in the other quantity also. Similarly, if one quantity decreases, the other quantity also decreases.
Hence, if “a” and “b” are two quantities, then the direction proportion is written as a∝b.
Inverse Proportion
The inverse proportion describes the relationship between two quantities in which an increase in one quantity
leads to a decrease in the other quantity. Similarly, if there is a decrease in one quantity, there is an increase
in the other quantity. Therefore, the inverse proportion of two quantities, say “a” and “b” is represented by
a∝(1/b).
Continued Proportion
Consider two ratios to be a: b and c: d.
Then in order to find the continued proportion for the two given ratio terms, we convert the means to a single
erm/number. This would, in general, be the LCM of means.
For the given ratio, the LCM of b & c will be bc.
Thus, multiplying the first ratio by c and the second ratio by b, we have
First ratio- ca:bc
Second ratio- bc: bd
Thus, the continued proportion can be written in the form of ca: bc: bd