PRACTICAL GEOMETRY
Practical geometry is an important branch of geometry which deals with the study of the size, positions, shapes as
well as dimensions of objects.
Geometrical Instruments
Whether you have to draw a line segment or measure it, draw a circle or arcs, draw an angle, etc. it can easily be
possible with the help of geometrical tools. Let us discuss the various geometrical instruments used in practical
geometry.

Points and Lines
Point: It is a location.
Line: Collection of points in a linear manner that extends infinitely in two directions.
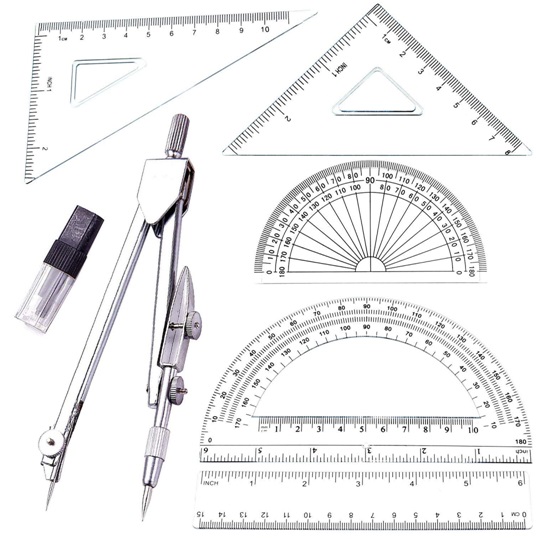
Tools of Construction
Tools used for construction:
Ruler: An instrument used to draw line segments and measure their lengths.
Compass: Instrument having a pointer on one end and a pencil on the other end.
It is used to mark equal lengths and to draw circles and arcs.
Divider: Instrument having a pair of pointers. It is used to compare lengths.
Set- Squares: Two triangular pieces – One of them has 45°, 45°, 90° and the other has
30°, 60°, 90° angles at the vertices. It is used to draw parallel and perpendicular lines.
Protractor: A semicircular instrument graduated into 180° parts. It is used to draw and measure angles.
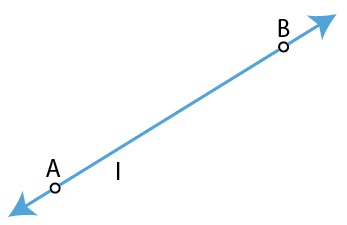
Line Segment
Line Segment: Part of a line that is bounded by two distinct endpoints.

Constructing a Line Segment for a given Length
Steps for constructing a line segment of a given length ‘a’:
(i) Draw a line l and mark a point A on it.

(ii) Place the compass on the initial point of the ruler. Open it to place pencil point up to the ‘a’ mark.
(iii) Place the pointer on A and draw an arc to cut l at B. AB is the required line segment.

Constructing Copy of a Line Segment
Steps for constructing a copy of a given line segment using ruler and compass together:
(i) Given AB whose length is unknown.
(ii) Fix compass’ pointer on A and pencil end on B. The opening of the instrument now gives the length of AB.
(iii) Draw any line l.
(iv) Placing the pointer on C, draw an arc that cuts l at a point say D. Then, CD = AB.
To know more about Constructing a Copy of a Line Segment, visit here.
Perpendiculars and Parallels
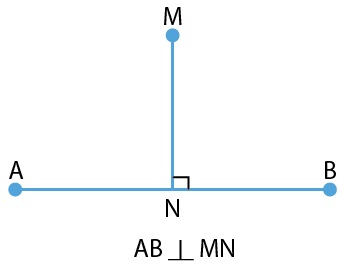
A line MN meeting another line AB at the right angle is said to be the perpendicular to the line AB.
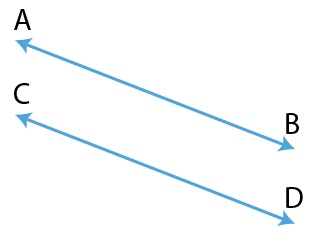
If two lines are non-intersecting and are always the same distance apart, then they are said to be parallel lines.
As shown in the figure, AB || CD.
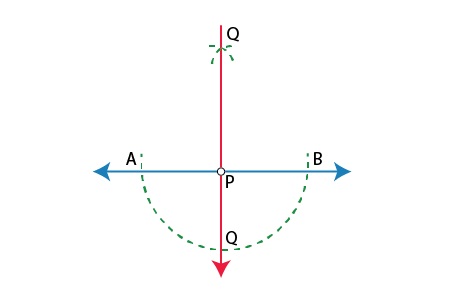
Constructing a Perpendiculars Using a Compass and Ruler
Steps for constructing perpendiculars using compass and rulers:
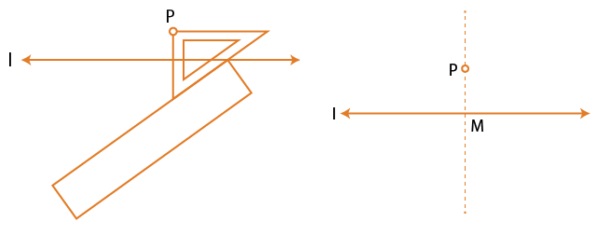
(i) Given a line I and a point P not on it.
(ii) With P as the centre, draw an arc which intersects line I at two points A and B.
(iii) Using the same radius and with A and B as centres, construct two arcs that intersect at a point, say Q, on the other side.
![]()
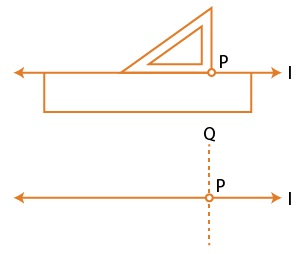
Constructing Perpendicular to a Line through a Point on the Line
Steps to construct a perpendicular to a line through a point on the line:
(i) Place a ruler along a given line l such that one of its edges is along l.
(ii) Place a set square with one of its edges along the already aligned edge of the ruler.
(iii) Slide the set square such that its right-angled corner coincides with the Point P.
(iv) Draw PQ and PQ are perpendicular to l.
Paper Folding Construction
Paper folding method to make perpendiculars:
(i) Let l be the given line and P be a point outside l.
(ii) Place a set-square on l such that one arm of its right angle aligns along l.
(iii) Place a ruler along the edge opposite to the right angle of the set-square.
(iv) Slide the set-square along the ruler till the point P touches the other arm of the set-square.
Circle
A circle is a set of all points in a plane that are equidistant from a point i.e. centre of the circle.
To know more about Circles,
Construction of a Circle for a given Radius
Steps for constructing a circle using a compass:
(i) Open compass for the required radius.
(ii) Place pointer of the compass on O.
(iii) Rotate the compass slowly to draw the circle.
Angle Bisector and Its Construction
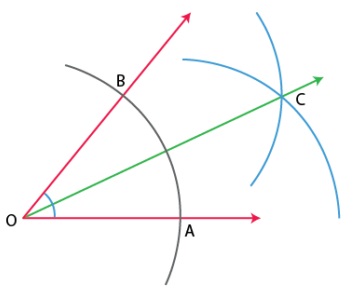
Steps to construct angle bisectors of a given angle:
(i) With O as the centre, draw an arc that cuts both rays at A and B.
(ii) With B as the centre, draw an arc whose radius is more than half of the length of AB.
(iii) With A as the centre, with the same radius, cut an arc in the interior of ∠BOA
(iv) Mark point of intersection as C. Then, OC is the angle bisector.
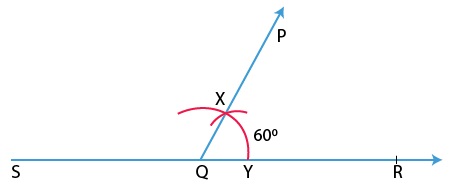
Construction of 30°, 60°, 90°and 120°Angles
(i) Construction of 60° angle:
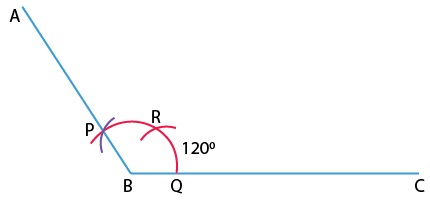
(ii) Construction of 120°angle:
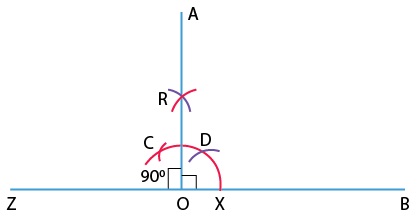
(iii) Construction of 90° angle:
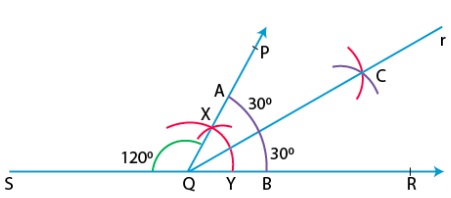
(iv) Construction of 30° angle:
Constructing of an Angle with Unknown Measurement
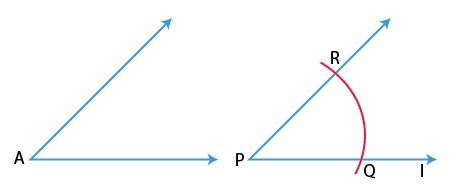
Steps for constructing a copy of an angle with unknown measurement:
(i) Draw a line l and choose a point P on it.
(ii) Place compass’ pointer at A and draw an arc to cut the rays of ∠A at B and C.
(iii) Draw an arc with P as the centre, cutting /at Q.
(iv) Set your compasses to length BC with the same radius.
(v) Place the compasses pointer at Q and draw an arc to cut the arc drawn earlier in R.
(vi) Join PR. This gives ∠P=∠A
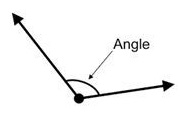
Angles
Angles: Formed by two rays sharing a common endpoint.