INTEGERS
Whole Numbers
Whole numbers include zero and all natural numbers i.e. 0, 1, 2, 3, 4, and so on.
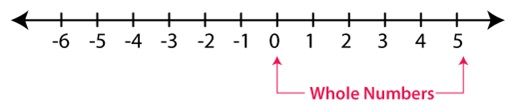
The whole numbers are the numbers without fractions and it is a collection of positive integers and zero. It is
represented by the symbol “W” and the set of numbers are {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,……………}. Zero as a
whole represents nothing or a null value.
• Whole Numbers: W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10……}
• Natural Numbers: N = {1, 2, 3, 4, 5, 6, 7, 8, 9,…}
• Integers: Z = {….-9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,…}
• Counting Numbers: {1, 2, 3, 4, 5, 6, 7,….}
These numbers are positive integers including zero and do not include fractional or decimal parts (3/4, 2.2 and 5.3
are not whole numbers). Addition, Subtraction, Multiplication and Division operations are possible on whole numbers.
Symbol
The symbol to represent whole numbers is the alphabet ‘W’ in capital letters.
W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…}
Thus, the whole numbers list includes 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ….
Facts:
• All the natural numbers are whole numbers
• All counting numbers are whole numbers
• All positive integers including zero are whole numbers
• All whole numbers are real numbers
Whole Numbers Properties
The properties of whole numbers are based on arithmetic operations such as addition, subtraction, division
and multiplication. Two whole numbers if added or multiplied will give a whole number itself. Subtraction
of two whole numbers may not result in whole numbers, i.e. it can be an integer too. Also, division of two
whole numbers results in getting a fraction in some cases. Now, let us see some more properties of whole
numbers and their proofs with the help of examples here.
Closure Property
They can be closed under addition and multiplication, i.e., if x and y are two whole numbers then x.
y or x + y is also a whole number.
Example:
5 and 8 are whole numbers.
5 + 8 = 13; a whole number
5 × 8 = 40; a whole number
Therefore, the whole numbers are closed under addition and multiplication.
Commutative Property of Addition and Multiplication
The sum and product of two whole numbers will be the same whatever the order they are added or multiplied in,
i.e., if x and y are two whole numbers, then x + y = y + x and x.y = y.x
Example:
Consider two whole numbers 3 and 7.
3 + 7 = 10
7 + 3 = 10
Thus, 3 + 7 = 7 + 3.
Also,
3 × 7 = 21
7 × 3 = 21
Thus, 3 × 7 = 7 × 3
Therefore, the whole numbers are commutative under addition and multiplication.
Additive identity
When a whole number is added to 0, its value remains unchanged, i.e., if x is a whole number then
x + 0 = 0 + x = x
Example:
Consider two whole numbers 0 and 11.
0 + 11 = 0
11 + 0 = 11
Here, 0 + 11 = 11 + 0 = 11
Therefore, 0 is called the additive identity of whole numbers.
Multiplicative identity
When a whole number is multiplied by 1, its value remains unchanged, i.e., if x is a whole number
then x.1 = x = 1.x
Example:
Consider two whole numbers 1 and 15.
1 × 15 = 15
15 × 1 = 15
Here, 1 × 15 = 15 = 15 × 1
Therefore, 1 is the multiplicative identity of whole numbers.
Associative Property
When whole numbers are being added or multiplied as a set, they can be grouped in any order,
and the result will be the same, i.e. if x, y and z are whole numbers then x + (y + z) = (x + y)
+ z and x. (y.z)=(x.y).z
Example:
Consider three whole numbers 2, 3, and 4.
2 + (3 + 4) = 2 + 7 = 9
(2 + 3) + 4 = 5 + 4 = 9
Thus, 2 + (3 + 4) = (2 + 3) + 4
2 × (3 × 4) = 2 × 12 = 24
(2 × 3) × 4 = 6 × 4 = 24
Here, 2 × (3 × 4) = (2 × 3) × 4
Therefore, the whole numbers are associative under addition and multiplication.
Distributive Property
If x, y and z are three whole numbers, the distributive property of multiplication over addition is x.
(y + z) = (x.y) + (x.z), similarly, the distributive property of multiplication over subtraction is x.
(y – z) = (x.y) – (x.z)
Example:
Let us consider three whole numbers 9, 11 and 6.
9 × (11 + 6) = 9 × 17 = 153
(9 × 11) + (9 × 6) = 99 + 54 = 153
Here, 9 × (11 + 6) = (9 × 11) + (9 × 6)
Also,
9 × (11 – 6) = 9 × 5 = 45
(9 × 11) – (9 × 6) = 99 – 54 = 45
So, 9 × (11 – 6) = (9 × 11) – (9 × 6)
Hence, verified the distributive property of whole numbers.
Multiplication by zero
When a whole number is multiplied to 0, the result is always 0, i.e., x.0 = 0.x = 0
Example:
0 × 12 = 0
12 × 0 = 0
Here, 0 × 12 = 12 × 0 = 0
Thus, any whole number multiplied by 0, the result is always 0.
Division by zero
Division of a whole number by o is not defined, i.e., if x is a whole number, then x/0 is not defined.
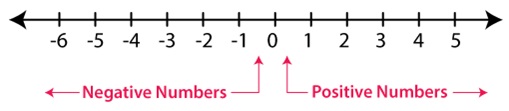
Numbers on a Number Line
Arithmetic operations of numbers can be better explained on a number line. To begin with, one must know
to locate numbers on a number line. Zero is the middle point of a number line. All (natural numbers) positive
numbers occupy the right side of the zero whereas negative numbers occupy the left side of zero on the number
line. As we move on to the left side value of a number decreases. For example, 1 is greater than -2. In a number
line, integers, fractions, and decimals can also be represented easily. Check out the links given below to learn more.

Negative Numbers
The numbers with a negative sign and which lies to the left of zero on the number line are called negative numbers.
Applications of Negative Numbers in Real Life
Irrespective of their value, they have a broad connection to daily life. These numbers are widely used in different fields.
Some of the real-life examples are given below.
Finance and Banking
Banking and financing are all about money, credit and debit. Hence, we need some numbers which can differentiate
a credit amount from the debit amount. Another instance is profit and loss. These all are mathematically denoted
by using positive and negative integers. If someone debited to someone it is represented by a minus sign. The
stock market is another field which widely uses negative integers to show its share price and ups and downs.
Science
Use of negative numbers is commonly observed in weather broadcasting. Thermometers are vertical number
lines which measure the temperature of a body as well as the temperature of an area. Meteorologist uses
negative numbers to show the cold condition of a region like -15˚C. Even when the body temperature goes
down a negative integer is used to represent the condition. Temperature below zero denoted with the negative
sign while a temperature above zero denoted with the positive sign. Other instruments and conditions that
depend on integers are batteries, blood pressure, overweight and underweight, drug testing and so on.
Other Applications
In sports, the goal differences in games like hockey, football are denoted by integers. Other examples are the
speed of a car, the rating of songs or movies, the numbering of a story of a building, etc.
Introduction to Zero
The number Zero
The number zero means an absence of value.
The Number Line
Integers
Collection of all positive and negative numbers including zero are called integers. ⇒ Numbers …,
– 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, … are integers.
Representing Integers on the Number Line
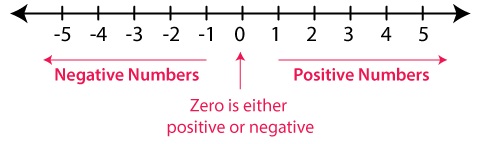
• Draw a line and mark a point as 0 on it
• Points marked to the left (-1, -2, -3, -4, -5, -6) are called negative integers.
• Points marked to the right (1, 2, 3, 4, 5, 6) or (+1, +2, +3, +4, +5, +6) are called positive integers.
Absolute value of an integer
• Absolute value of an integer is the numerical value of the integer without considering its sign.
• Example: Absolute value of -7 is 7 and of +7 is 7.
Ordering Integers
• On a number line, the number increases as we move towards right and decreases as we move towards left.
• Hence, the order of integers is written as…, –5, –4, – 3, – 2, – 1, 0, 1, 2, 3, 4, 5…
• Therefore, – 3 < – 2, – 2 < – 1, – 1 < 0, 0 < 1, 1 < 2 and 2 < 3.
Addition of Integers
Positive integer + Negative integer
Example: (+5) + (-2) Subtract: 5 – 2 = 3 Sign of bigger integer (5): + Answer: +3
Example: (-5) + (2) Subtract: 5-2 = 3 Sign of the bigger integer (-5): – Answer: -3
Positive integer + Positive integer
Example: (+5) + (+2) = +7
Add the 2 integers and add the positive sign.
Negative integer + Negative integer
Example: (-5) + (-2) = -7
Add the two integers and add the negative sign.
Properties of Addition and Subtraction of Integers
Operations on Integers
Operations that can be performed on integers:
• Addition
• Subtraction
• Multiplication
• Division.
Subtraction of Integers
The subtraction of an integer from another integer is same as the addition of the integer
and its additive inverse.
Example: 56 – (–73) = 56 + 73 = 129 and 14 – (8) = 14 – 8 = 6
Properties of Addition and Subtraction of Integers
Closure under Addition
a + b and a – b are integers, where a and b are any integers.
Commutativity Property
a + b = b + a for all integers a and b.
Associativity of Addition
(a + b) + c = a + (b + c) for all integers a, b and c.
Additive Identity
Additive Identity is 0, because adding 0 to a number leaves it unchanged.
a + 0 = 0 + a = a for every integer a.
Multiplication of Integers
• Product of a negative integer and a positive integer is always a negative integer. 10 × − 2 = −20
• Product of two negative integers is a positive integer. −10 × −2 = 20
• Product of even number of negative integers is positive. (−2) × (−5) = 10
• Product of an odd number of negative integers is negative. (−2) × (−5) × (6) = −60
Properties of Multiplication of Integers
Closure under Multiplication
Integer × Integer = Integer
Commutativity of Multiplication
For any two integers a and b, a × b = b × a.
Associativity of Multiplication
For any three integers a, b and c, (a × b) × c = a × (b × c).
Distributive Property of Integers
Under addition and multiplication, integers show the distributive property.
For any integers a, b and c, a × (b + c) = a × b + a × c.
Multiplication by Zero
For any integer a, a × 0 = 0 × a = 0.
Multiplicative Identity
1 is the multiplicative identity for integers.
a × 1 = 1 × a = a
Division of Integers
(positive integer/negative integer)or(negative integer/positive integer)
⇒ The quotient obtained is a negative integer.
(positive integer/positive integer)or(negative integer/negative integer)
⇒ The quotient obtained is a positive integer.
Properties of Division of Integers
For any integer a,
• a/0 is not defined
• a/1=a
Integers are not closed under division.
Example: (–9)÷(–3)=3 result is an integer but (−3)÷(−9)=−3−9=13=0.33 which is not an integer.
To know more about Number Lines,
