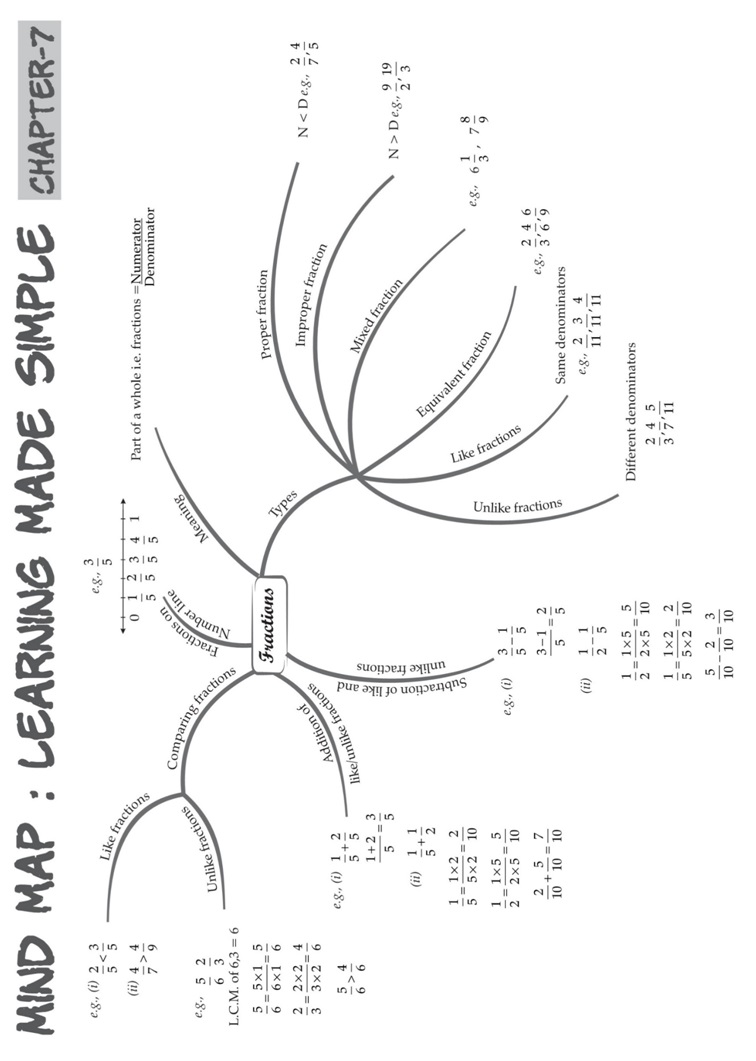
FRACTIONS
Fraction Definition
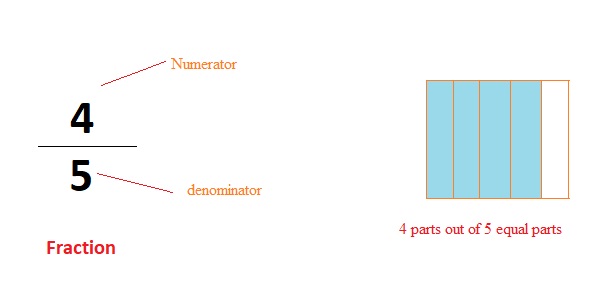
A fraction is a number representing a part of a whole. The whole may be a single object or a group of objects.
Suppose Ramesh has a chocolate and we want to equally share with his Friend Amit. He will divide the chocolate into
two pieces and keep one piece with him and give another piece to Amit. So basically they each have got 1 part out of
2 parts i.e 1/2 of the chocolate. Similarly if they have another suresh also, then they will divide chocolate in three
equal parts,then each of them will have 1 out of 3 parts i.e 1/3 of the chocolate
Important Note:
When expressing a situation of counting parts to write a fraction, it must be ensured that all parts are equal.
Types of Fractions
Fractions are of three types.
(a.) Proper Fraction
(b.) Improper Fraction
(c.) Mixed Fraction.
proper Fraction:
Proper Fraction is the fraction which is less than 1 or where Numerator is less than Denominator
Here the Denominator shows the part whole has been divided and numerator shows the part
which has been considered.This is the same fraction which we discussed with fraction definition
Example;
1/3
2/3
4/3
Improper Fraction: Improper Fraction is the fraction which is greater than 1 or where Numerator is
greater than Denominator Lets understand this with example. Suresh has 5 chocolates and he has to
divide those chocolate among four friends. We can divide each chocolate into fours parts and each
one can have one-quarter part of the each chocolate.So Each friend will be having 5 parts of the one-
quarter part.Now 4 parts make one whole. So basically each one of them
is getting 1 whole and 1 part. So this can be written as 5/4
Here numerator is more than denominator
Example:
11/5
5/4
10/9
Mixed Fraction:
It is combination of whole number and proper fraction
8 4/9
Lets the example of improper fraction only. The division can made in another way. We give one
chocolate to each of them and divide the fifth chocolate into four pieces. So each of them got
1 full chocolate and one-quarter part of last chocolate. So, this can written as
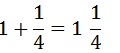
This is mixed fraction.
![]()
Example:
![]()
Convert Improper Fractions to Mixed Fraction

Example

How to convert Improper Fractions to Mixed Fraction

Example

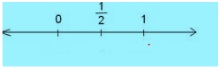
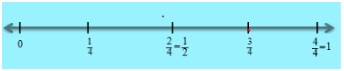
How to Represent Fraction on Number Line?
We can show fractions on a number line. In order to represent 1/2 on the number line, draw the
number line and look for the portion between 0 and 1 Now, divide the gap between 0 and 1 into
two equal parts. The point of division represents 1/2.
To represent 1/4 on a number line, we divide the gap between 0 and 1 into 4 equal parts
First point will represent ½
Second point will represent 2/4 =1/2
Third point will represent ¾
Simplest Form of a Fraction
If the numerator and the denominator of a fraction have no common factor except, then it is
said to be in its simplest form or lowest form.
Example
1/3
2/3
Equivalent fractions
Equivalent fractions are fractions that have the same value in its simplest form.
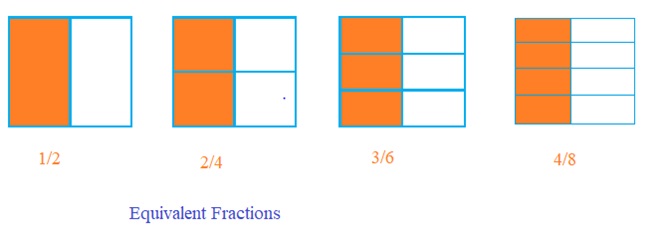
Example
2/6 ,1/3 ,6/18are equivalent fractions as they have same value
The equivalent fraction of a given fraction is obtained by multiplying both the numerator and
the denominator of the given fraction by the same number.
Checkout Equivalent Fraction calculator
Example
2/3
Equivalent Fraction can be obtained by multiplying both the numerator and the denominator
of the given fraction by the same number.
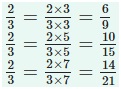
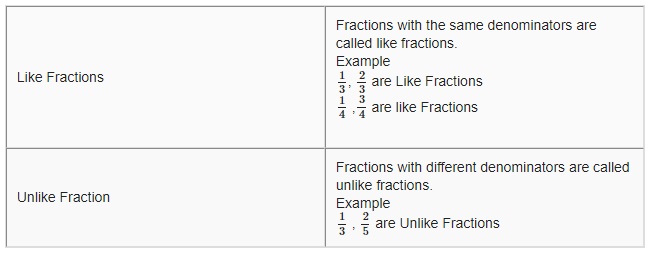
Like Fractions and Unlike Fractions
Comparing Fractions
We often come across a situation where we need to compare fractions.There is systematic procedure
available for Comparing Fractions. It is divided into two Comparing Like Fraction which is easy and
other is Comparing unlike Fraction. lets take a deep dive into it
Comparing Like Fraction
The numerator value decides the larger value.
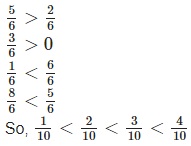
Comparing Unlike Fraction
We can further divide into two parts.
Comparing fractions with same numerator
For fractions having same numerator, the fraction with the lowest denominator is the greater number
Example
2/5 and 2/7
Here 5 < 7
So 2/5 > 2/7
Comparing fractions with different denominator and numerator
Here we would be using the technique of equivalent fractions. We would convert each of the fraction
into equivalent fraction such that they become like fractions.Then comparison is simple. So here are the steps
1. Find the LCM of the denominators
2. Convert each fraction into equivalent fraction such that denominator is the LCM.
3. Now both the fraction are converted into Like fraction,so we can do the comparison easily

How to Add Fractions
We often come across a situation where we need to add fractions.There is systematic procedure available
for adding Fractions. It is divided into two parts Adding Like Fraction which is easy and other is Adding
unlike Fraction. lets take a deep dive into it.
Adding Like Fraction
Addition: The numerator adds to provide the final fraction value.
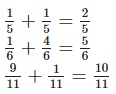
Adding Unlike Fraction
First, we need to convert the unlike fraction to like fraction using the LCM of the denominators and
convert each fraction into like fraction using the LCM
And then it works like “like” Fraction
Let us check few examples to make it clear

How to Subtract Fractions
We often come across a situation where we need to subtract fractions.There is systematic procedure
available for subtract Fractions. It is divided into two parts Subtracting Like Fraction which is easy and
other is Subtracting unlike Fraction. lets take a deep dive into it
Subtracting Like Fraction
Subtraction: The Numerator subtract to provide the final fraction value.
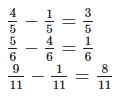
Subtracting UnLike Fraction
First we need to convert the unlike fraction to like fraction using the LCM of the denominators and
convert each fraction into like fraction using the LCM
And then it works like “like” Fraction
Let us check few example to make it clear

Comparison, Addition and Subtraction of Mixed Fractions
Two mixed fractions can be added or subtracted by adding or subtracting the whole number of the
two fractions and then adding or subtracting the fractional parts together.
Two mixed fractions can also be converted into improper fractions and then added or subtracted.