WHOLE NUMBERS
• Counting numbers are called natural numbers. Natural numbers are denoted by N and given by
N = {1, 2, 3, 4, ...}
• Natural numbers included with '0' are called whole numbers. Whole numbers are represented by W
and given by W = {0, 1, 2, 3, 4, ...}
• A number which comes after a given number is called its successor.
Successor = given number + 1
• A number which comes before a given number is called its predecessor.
Predecessor = given number – 1
• Every whole number has a successor. Every whole number except 0, has apredecessor.
• The following number line represents a whole number line on which whole numbers are represented.

The distance between two points is called unit distance.
Number operations of addition, subtraction and multiplication can easily be performed on number line.
• Closure Property for addition and multiplication: If we add or multiply two whole numbers the result is again a whole number.
Closure property does not hold good for subtraction and division of whole numbers.
• Commutativity of addition and multiplication: Whole number can be added or multiplied in any order.
That is, for any two whole numbers 'a' and 'b', a + b = b + a and a × b = b × a
Commutative property does not hold good for subtraction and division of whole numbers.
• Associativity of addition and multiplication: Whole numbers can be grouped for the convenience of
adding or multiplying. That is, for any three whole numbers 'a' , 'b' and 'c',a + (b + c) = (a+ b) + c and a × (b × c) = (a × b) × c
Associative property does not hold good for subtraction and division of whole numbers.
• Distributivity of multiplication over addition: For any three whole numbers 'a' , 'b' and 'c', a × (b + c) = (a × b) + (a × c)
• Identity for addition: 0 is the identity for addition; this means when 0 is added to any whole the result is the whole number itself.
• Identity for multiplication: 1 is the identity for multiplication; this means when 1 is multiplied with any whole number
the result is the whole number itself.
• Division of a whole number by zero is not defined
Whole Numbers
The numbers 1,2, 3, are called natural numbers or counting numbers.
Let us add one more number i.e., zero (0), to the collection of natural numbers. Now the numbers
are 0,1,2, … These numbers are called whole numbers
We can say that whole nos. consist of zero and the natural numbers. Therefore, except zero all the
whole nos. are natural numbers.
Facts of Whole numbers
• The smallest natural number is 1.
• The number 0 is the first and the smallest whole nos.
• There are infinitely many or uncountable number of whole-numbers.
• All natural numbers are whole-numbers.
• All whole-numbers are not natural numbers. For example, 0 is a whole-number but it is not a natural number.
The first 50 whole nos. are
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,14, 15, 16, 17, 18, 19, 20, 21,
22, 23, 24, 25,26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40,
41, 42, 43, 44, 45, 46, 47, 48, 49, 50
Number line
A number line is a picture of a graduated straight and horizontal line in which numbers are written. A number
written on the left-hand side of the number line is lesser and number written on the right-hand side of the number
line is greater. Lets us look into some solved example problems.

In the above figure, we can see a number line where integers are placed. Here, the positive and negative integers
are placed on either side of the zero.
Find 12 × 35 using distributivity.
12 × 35 = 12 × (30 + 5)
= 12 × 30 +12 × 5
= 360 + 60 = 420.
Calculate – (2 + 3) + 4 =? = 5+ 4 = 9.
A number line is a pictorial representation of numbers on a straight line. It’s a reference for comparing and ordering
numbers. It can be used to represent any real number that includes every whole number and natural number. Just to
recollect, the whole number is a set of numbers that include all counting numbers (1, 2, 3,4,5,6 …….) and zero (0),
whereas the natural number is the set of all counting numbers i.e. 1, 2, 3, 4, 5, 6……..
Writing numbers on a number line make it easier to compare the numbers. From the above figure, we can see that
the integers on the left side are smaller than the integers on the right side. For example, 0 is less than 1, -1 is less
than 0, -2 is less than -1, and so on.
Numbers on a Number Line
Arithmetic operations of numbers can be better explained on a number line. To begin with, one must know to locate
numbers on a number line. Zero is the middle point of a number line. All (natural numbers) positive numbers occupy
the right side of the zero whereas negative numbers occupy the left side of zero on the number line. As we move on to
the left side value of a number decreases. For example, 1 is greater than -2. In a number line, integers, fractions, and
decimals can also be represented easily. Check out the links given below to learn more.
Number Line 1 to 100
Here are the number lines from 1 to 100 numbers. As we already we can extend the number line indefinitely, thus
students can also try to draw the line beyond 100, to practice.

Addition on Number Lines
Adding Positive Numbers
When we add two positive numbers, the result will always be a positive number. Hence, on adding positive numbers
direction of movement will always be to the right side.
For example, addition of 1 and 5 (1 + 5 = 6)
Here the first number is 1 and the second number is 5; both are positive. First, locate 1 on the number line.
Then move 5 places to the right will give 6.
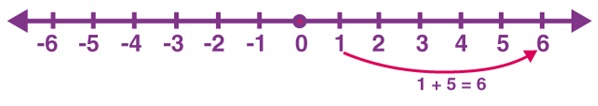
Adding Negative Numbers
When we add two negative numbers, the result will always be a negative number. Hence, adding negative
numbers direction of movement will always be to the left side.
For example, the addition of -2 and -3
Here, the first number is -2 and the second number is -3; both are negative. Locate -2 on the number line.
Then move 3 places to the left will give -5.

Some other Important terms to remember

Properties of Whole Numbers
Closure Property
Closure property on Addition for Whole Number
0 + 2 = 2
1 + 3 = 4
5 + 6 = 11
So Whole number are closed on Addition
Closure property on Multiplication for Whole Number
0 × 2 = 0
1 × 4 = 4
5 × 1 = 5
So Whole number are closed on Multiplication
Closure property on subtraction of Whole number
5 – 0 = 5
0 – 5 =?
1 – 3 =?
3 – 1 = 2
So Whole number are not closed on Subtraction
Closure property on Division of Whole number
2/1=2
1/2=?
0/2=0
2/0=?(Division by Zero is undefined)
So Whole Number are not closed on Division
In short
Closure Property
If a and b are any two whole numbers, then a+b, a × b are also whole numbers.
Commutative property
Commutativity property on Addition for Whole Number
So Whole number are Commutative on Addition
0 + 2 = 2 + 0 = 2
Commutativity property on Multiplication for Whole Number
0×2=0or2×0=0
So Whole number are Commutative on Multiplication
Commutativity property on subtraction of Whole number
5 – 0=5but 0 – 5=?
So Whole number are not Commutative on Subtraction
Commutativity property on Division of Whole number
2/1=2 but 1/2=?
So Whole Number are not Commutative on Division
In short
You can add two whole numbers in any order. You can multiply two whole numbers in any order.
Commutative property: If a and b are any two whole numbers, then a + b = b + a and a × b = b × a
Associative property
Associativity property on Addition for Whole Number
0+(2+3)=(0+2)+3=50+(2+3)=(0+2)+3=5
1+(2+3)=6=(1+2)+31+(2+3)=6=(1+2)+3
So Whole number are Associative on Addition
Associativity property on Multiplication for Whole Number
0×(2×3)=0 or(0×2)×3 = 0
So Whole number are Associative on Multiplication
Associativity property on subtraction of Whole number
10 – (2 – 1) = 9 but (10 - 2) – 1 = 7
So Whole number are not Associative on Subtraction
Associativity property on Division of Whole number
16÷(4÷2)=8 but (16÷4)÷2=2
So Whole Number are not Associative on Division
So in Short
If a, b and c are any two whole numbers, then (a+b)+c = a+(b+c) and (a×b)×c = a×(b×c).
Distributive property
If a, b and c are any two whole numbers, then a (b + c) = a × b + a × c
Additive Identity
If a is any whole number, then a + 0 = a = 0 + a
Example
2 + 0 = 2
0 + 3 = 3
5 + 0 = 5
Multiplicative Identity
If a is any whole number, then a × 1 = a = 1 × a
Example
1 × 1 = 1
5 × 1 = 5
6 × 1 = 6
Multiplication by zero
If a is any whole number, then a × 0 = 0 = 0 × a
Example
1 × 0 = 0
5 × 0 = 0
0 × 0 = 0
Division by zero
If a is any whole number, then a ÷ 0 is not defined
