Leave Comment

CBSE 10th CLASS MATHS CHAPTER QUADRATIC EQUATIONS

Standard form of Quadratic Equations

An equation of the form ax2 + bx + c = 0 where a, b, c Complex number and a 0 is called a quadratic equation. The numbers a, b, c

are called the coefficients of this equation and x is real variable, here a is coefficient of x2, b is coefficient of x & c is constant term.
* Real Quadratic Equation : An Equation ax2 + bx + c = 0, a 0 & a, b, c R is called “Real Quadratic Equation.”

* Monic Quadratic Equation : If the co-efficient of x2 be unity, then the quadratic equation is called “Monic Quadratic Equation”.

* Properties of Quadratic Equations
A quadratic equation has two and only two roots.

A quadratic equation cannot have more than two different roots.
If a is a root of the quadratic equation ax² + bx + c = 0, then (x–a) is a factor of ax² + bx + c = 0.
If the roots a & b be reciprocals to each other, then a = c.
If the two roots a & b be equal in magnitude and opposite in sign, then b = 0
· .
· If a > 0, then minimum value of ax² + bx + c = 0 is (4ac – b²) / 4a.
· If a < 0, then maximum value of
ax² + bx + c = 0 is (4ac – b2) / 4a.
· If c = 0 one root is zero other is .
· If b = c = 0 both roots are zero.

Note : The possible values of x which satisfy the quadratic equation are called the roots of the quadratic equation.

* Roots of a Quadratic Equation : Let p(x) = 0 be a quadratic equation, then the zeros of the polynomial p(x) are called the roots of the equation p(x) = 0.
Thus a is a root of p(x) = 0, if p(a) = 0
Also, x = a is called a solution of the given equation.

* Solving of a Quadratic Equation by Factorization Method :
Let ax² + bx + c = 0 be a quadratic equation and let the quadratic polynomial ax² + bx+ c be expressible as a product of two linear factors, say (dx + e)

and (fx + g) where d, e, f, g are real numbers such that d 0 and f 0.
   Then,
   ax² + bx + c   =   0
   (dx + e) (fx + g) =   0
   dx + e       =   0 or fx + g = 0
    x = -e/d and x=-g/f are the possible roots of the quadratic equation ax2 + bx + c = 0.

   Solving of a Quadratic Equation by Quadratic Formula :
   Consider the general quadratic equation
   ax² + bx + c = 0

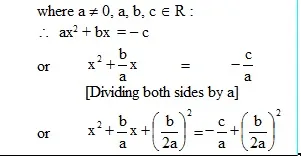
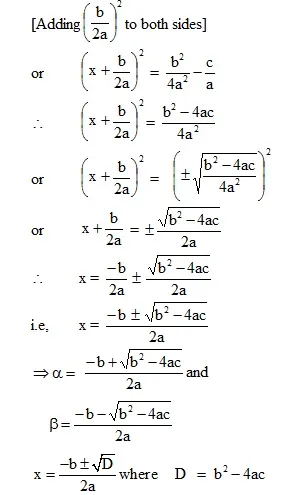
   This is also called Sridharacharya formula.
   Thus, the equation ax² + bx + c = 0 has two roots a and b, given by.
   Discriminant : b² – 4ac determines the nature of the roots of the quadratic equation,

it is called the ‘DISCRIMINANT’ of the quadratic equation.

Nature of the roots :

* Condition for Common Roots :
   Consider two quadratic equations
a₁x² + b₁x + c₁ = 0   ...(i)    a10
and   a₂x² + b₂x + c₂ = 0   ...(ii)    a20
(A)    If one root is common then,
   (a₁b₂ – a₂b₁) (b₁c₂ – b₂c₁) = (c₁a₂ – c₂a₁)2
(b)   If two roots are common then,
a1/a2 = b1/b2 = c1/c2

* Sum of the roots of a Quadratic Equation:




* Product of the roots of a quadratic equation :






* Roots of cubic and quadratic equations (optional) :

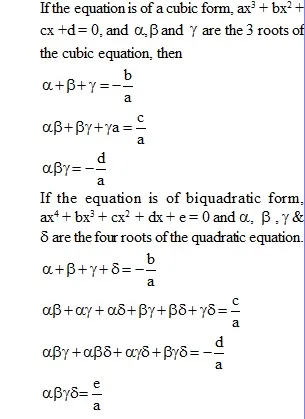
* Formation of a quadratic equation :

* Relation Between Roots and Coefficient:
   If roots of quadratic equation
   ax² + bx + c = 0 (a 0) are then:

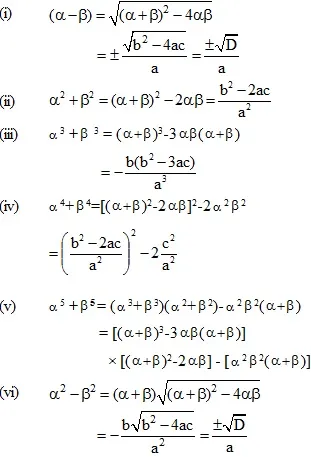
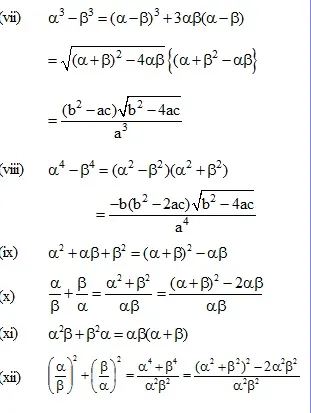
3. Relationship between discriminant & nature of the roots :
If ax² + bx + c = 0, a0 is a quadratic equation, then the expression, b² – 4ac is known as its discriminant and denoted by D.

· If a, b, c R and p + iq is one root of quadratic equation (where q 0), then the other root must be conjugate p – iq and vice–versa. (p, q, R and i = $\sqrt{-1}$ )
· If a, b, c Q and p + $\small \sqrt{q}$ is one root of the quadratic equation, then the other root must be the conjugate p – $\small \sqrt{q}$ and vice–versa (where p is a rational and $\small \sqrt{q}$ is a surd.
· If a = 1 and b, c I and the roots of quadratic equation are rational numbers, then these roots must be integers.
· If the quadratic equation has more than 2 roots (complex numbers), then the equation becomes an identity i.e., a = b = c = 0.
· The condition that a quadratic function f (x, y) = ax² + 2 hxy + by² + 2 gx + 2 fy + c may be resolved into two linear factors is that;

abc + 2 fgh – af² – bg² – ch² = 0
or 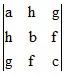= 0.
When D 0, then the equation ax² + bx + c = 0 is factorizable into two linear factors.
i.e., ax² + bx + c = 0 (x – a)(x –b) = 0, i.e. a (x – a)(x –b) where a and b are the roots of quadratic equation.

* Formation of a Quadratic Equation
   Let a, b be the two roots, then we can form a quadratic equation as follows :
   x² – (Sum of roots)x + (Product of roots) = 0
   i.e.,   x² – (a + b)x + (ab) = 0
   or     (x – a) (x – b) = 0
* Sign of the Roots :
1.   The roots a, b are both negative, if (a + b) and a b are both positive
   (i.e., if -b/a and c/a are both positive.)
2.   The roots a, b are both positive, if (a + b) is negative and ab is positive
   (i.e., if is negative and is positive.)
3.   The roots a, b are of opposite signs, ab is negative (i.e., is negative)

4.   If sign of a = sign of b sign of c Greater root's magnitude is negative.
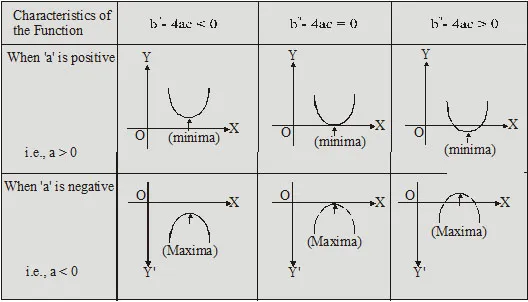
* Maximum or minimum value of a quadratic expression :
   The quadratic expression ax² + bx + c takes different values as x takes different values.
   For all the values of x, as x varies from – $\small \infty$ to + $\small \infty$ . (i.e., when x is real), the quadratic expression ax² + bx + c.
(i)    has a minimum value if a > 0. (i.e., a is positive). The minimum value of the quadratic expression is (4ac-b²)/4a and it occurs at . x= -b/2a
(ii)    has a maximum value if a < 0. (i.e., a is negative). The maximum value of the quadratic expression is (4ac-b²)/4a and it occurs at . x= -b/2a

* Graph of a Quadratic Functions ax²+bc+c = 0,a 0

The graph of a quadratic function (expression) is called a parabola. The point at which its direction changes is called its turning point,
commonly called the vertex of the parabola.
The graph of the function is concave upwards when a > 0 and concave downwards when a < 0.
If the graph has no points in common with the x-axis, the roots of the equation are imaginary and cannot be determined from the graph.
If the graph is tangent to the x-axis, the roots are real and equal.
If the graph cuts the x-axis, the roots of the equation will be real and unequal. Their values will be given by the abscissa of the points
of intersection of the graph and the x-axis.

5. Solution of ax2 + bx + c = 0 by various methods :
· Factorization :
Let ax² + bx + c = 0 by the given quadratic equation. Assume that (ax² + bx + c) be expressible as the product of two linear factors namely

(lx + m) and (px + q) where l, m, p, q are real numbers such that l 0, p 0. Then ax² + bx + c = 0 (lx + m) (px + q) = 0
   Either lx + m = 0    or    px + q = 0
   lx = – m    or    px = – q
   x = – m/l or    x = – q/p

* Completing the square :
Step 1.   Consider the standard quadratic equation : ax² + bx + c = 0, (a 0)
Step 2.   Transpose the constant term (c) to the other side (RHS).
Step 3. Make the coefficient of x² as unity. Divide both sides by coefficient of x² i, e., by a
Step 4. Make the L.H.S. as perfect square or completing the square of L.H.S. by adding both sides

Step 5. Taking square-root of both sides. Take both the signs.
Step 6. Obtain two values of the variable (x).

Solutions of Equations Reducible to Quadratic Form
Equation which at the outset are not quadratic equations but can be reduced to quadratic equations by using suitable algebraic transformations.

Such equations are called equations reducible to quadratic equations. Some of the common types are :

· ax⁴ + bx² + c = 0
This can be reduced to a quadratic equation by substituting x2 = y. i.e., ay2 + by + c = 0.

Type 1 : Equations of the Form :
ax⁴ + bx² + c = 0.

   Algorithm to solve equation of the form
   ax⁴ + bx² + c = 0
Step 1 : Obtain the given equation.
Step 2 : Replace x2 by y and x4 by y2 in the given equation to obtain a quadratic equation in y.
Step 3 : Solve the quadratic equation in y by any one of the methods of solving a quadratic equation.
Step 4 : Obtain the positive values of y. Let the values of y be a and b.
Step 5 : Solve the equations x2 = a and x2 = b.
Step 6 : The values of x obtained in step V constitute the solution set of the given equation.
   Example : Solve 2x⁴ – 5x² + 3 = 0.
   Solution : Putting x2 = y, the given equation reduces to
   2y2 – 5y + 3 = 0 2y2 – 2y – 3y + 3 = 0
           2y (y – 1) – 3 (y – 1) = 0
           (2y – 3) (y – 1) = 0
           2y – 3 = 0 or y – 1 = 0
           y = 3/2 or y = 1
   Now, y = 3/2 x2 = 3/2
              x= $\small \pm \sqrt{3/2}$
   And, y = 1     x² = 1
           x = ± 1.
   Hence, the roots of the given equation are 1, – 1,. $\small \sqrt{3/2},-\sqrt{3/2}$
Type 2 : Equatins of the form
   a {p(x)}2 + b. p(x) + c = 0, where p(x) is an expression in x and a, b, c are real numbers.

Algorithm to solve equations of the form a {p(x)}2 + b {p(x) + c = 0, where p(x) is an expression in x and a, b, c Î R.

Step 1 : Obtain the equation. Let the equation be a {p(x)}² + b {p(x)} + c = 0, where a, b, c Î R.
Step 2 : Put p(x) = y, {p(x)}² = y₂ in the equation obtained in step 1 to get the quadratic ay² + by + c = 0.
Step 3 : Solve the quadratic in y obtained in step 2 by any one of the methods of solving quadratic equations. Let the values be y = a and y = b.
Step 4 : Solve the equations p(x) = a and p(x) = b for x.
Step 5 : The values of x obtained in step IV constitute the solution set of the given equation.

Example :Solve : (x²+3x)² - (x²+3x)-6 = 0 x R.
Solution : Putting x² + 3x = y, the given equation reduces to y² – y – 6 = 0
   Now,
   y² – y – 6 = 0 y2 – 3y + 2y – 6 = 0
           y (y – 3) + 2 (y – 3) = 0
           (y – 3) (y + 2) = 0
           y – 3 = 0 or y + 2 = 0
y = 3 or y = – 2
   x2 + 3x = 3 x2 + 3x – 3 = 0

   And, y = – 2   x² + 3x = – 2
           x² + 3x + 2 = 0
           x² + 2x + x + 2 = 0
           x (x + 2) + 1 (x + 2) = 0
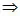           (x + 2) (x + 1) = 0
           x + 2 = 0 or x + 1 = 0
           x = – 2 or x = – 1
   Hence, the roots of the given equation are – 2, – 1,

Type 3 : Equations of the form

ap(x)+b/P(x) = c, where p(x) is an expression in x and a, b, c are real numbers.

Algorithm to solve equations of the form ap(x)+b/P(x) = c, where p(x) is an expression in x and a, b, c are real numbers.

Step 1 : Obtain the given equation. Let the equation be ap(x)+b/P(x) = c
Step 2 : Put p (x) = y in the equation in step 1 to obtain the quadratic a y² – cy + b = 0.
Step 3 : Solve the quadratic in step 2 by any one of the methods discussed in previous sections. Let the values of y be a and b.
Step 4 : Solve the equation p(x) = a and p(x) = b for x.
Step 5 : The values of x obtained in step 4 constitute the solution set of the given eqaution.
Following examples will illustrate the above algorithm.

Example : Solve : x/(x+1) + (x+1)/x = 34/15
Solution : Putting x/(x+1) = y and (x+1)/x = 1/y. The given equation reduces to
y+1/y = 34/15  y²+1/y = 34/15
   15 y² – 34y + 15 = 0.
   Now, 15 y² – 34y + 15 = 0
   15 y² – 25y – 9y + 15 = 0
   5y (3y – 5) – 3 (3y – 5) = 0
   (3y – 5) (5y – 3) = 0
   3y – 5 = 0 or 5y – 3 = 0
   y = 5/3 or y = 3/5
   Now, y = 5/3 x/(x+1) = 5/3 3x = 5x+5
       2x = – 5 x = – 5/2
   And, y=3/5 x/(x+1) = 3/5 5x=3x+3
       2x = 3   x=3/2
   Hence, the roots of the given equation are 3/2 and -5/2

Type 4 : Equations of the form
(i)
(ii)

   Algorithm to solve equations of the form
(i)    and

Step 1 : Obtain the equation.
Step 2 : If the coefficient of b in the given equation contains x+1/x then replace x²+1/x²by (x+1/x)² -2 and put x+1/x = y

In case the coefficient of b is x-1/x is then replace x²+1/x² by (x-1/x)² +2

and put x-1/x = yy
Step 3 : Solve the quadratic equation in y obtained in step 2.
Step 4 : Equate the values of y obtained in step 3 to x+1/x or x-1x as the case may be and obtain a quadratic equation in x.
Step 5 : Solve the quadratic equations obtained in step 4. The values of x so obtained consititute the solution set of the given equation.
Following examples illustrate the above alogrithm.
Example : Solve :
9(x²+1/x²) - 9(x+1/x)-52 = 0
Solution : Let x+1/x =y Then
(x+1/x)² = y² x²+1/x²+2 = y²

x²+1/x² = y²-2

   Substitution
x+1/x = y and x²+1/x² = y²-2 in the given equation, it becomes.
   9 (y² – 2) – 9y – 52 = 0
       9y² – 9y – 70 = 0
       9y² – 30 y + 21y – 70 = 0
       3y (3y – 10) + 7 (3y – 10) = 0
       (3y – 10) (3y + 7) = 0
       3y – 10 = 0 and 3y + 7 = 0
         y = 10/3 and y = -7/3
   Now,

   3x² + 3 = 10 x 3x² – 10x + 3 = 0
   3x² – 9x – x + 3 = 0
   3x (x – 3) – 1 (x – 3) = 0
   (3x – 1) (x – 3) = 0
   3x – 1 or x – 3 = 0
   x = 1/3 or x = 3.
   And,
y= -7/3 x+1/x = -7/3 x²+1/x = -7/3
   3x² + 3 = – 7x
   3x² + 7x + 3 = 0

   Hence, the roots of the given equation are

Type 5 : Equations of the form
(x + a) (x + b) (x + c) (x + d) + k = 0, where a, b, c, d k 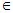R such that a + b = c + d.

Algorithm to solve equations of the form (x + a) (x + b) (x + c) (x + d) + k = 0, where a, b, c, d, k R such that a + b = c + d.

Step 1 : Obtain the equation (x + a) (x + b) (x + c) (x + d) + k = 0.
Step 2 : Re-write the given equation in the form {(x + a) (x + b) } × { (x + c) (x + d) } + k = 0.
Step 3 : Put x² + x (a + b) = x² + x (c + d) = y and obtain a quadratic in y i.e.
(y + ab) (y + cd) + k = 0.
Step 4 : Solve the quadratic obtained in step 3. Let the value of y be y1 and y2.
Step 5 : Equate x² + x (a + b) to y1 and y2 to obtain two quadratic equation in x. The values of x so obtained form

the solution set of the given equation.
Following examples illustrate the above algorithm.

Example : (x + 1) (x + 2) (x + 3) (x + 4) = 120.
Solution : Since 1 + 4 = 2 + 3. So, we write the given equation in the following form :
   {(x + 1) (x + 4)} {(x + 2) (x + 3)} = 120 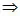(x2 + 5x + 4) (x2 + 5x + 6) = 120
   Putting x² + 5x = y. The above equation becomes
   (y + 4) (y + 6) = 120 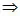y² + 10y + 24
   = 120
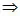       y2 + 10y – 96 = 0
       y2 + 16y – 6y – 96 = 0
       y (y + 16) – 6 (y + 16) = 0
       y + 16 = 0 or y – 6 = 0
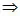       y = – 16 or y = 6
   Now, y = – 16 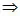  x² + 5x = – 16
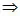           x² + 5x + 16 = 0
   Clearly, discriminant of this equation is negative. So, it has no real solution.
   And, y = 6
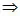       x2 + 5x = 6 Þ x2 + 5x – 6 = 0
        x2 + 6x – x – 6 = 0
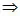       x (x + 6) (x – 1) = 0
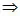       x + 6 = 0 or x – 1 = 0
       x = – 6 or x = 1
   Hence, the roots of the given equation are – 6 and 1.

Type 6 : Equations of the form $\small \sqrt{ax+b}=cx+d$ where a, b, c, d 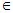R.

Algorithm to solve equations of the form $\small \sqrt{ax+b}=cx+d$

Step 1 : Obtain the equation. Let the equation be $\small \sqrt{ax+b}=cx+d$
Step 2 : Square both sides to obtain ax + b = (cx + d)² or c² x² + (2 cd – a) x + d² – b = 0.
Step 3 : Solve the quadratic equation obtained in step 2.
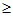Step 4 : Reject those values of x, obtained in step 3, which do not satisfy both ax + b 0 and cx + d 0.

The remaining values of x obtained in step 3 form the solution set of the given equation.

NOTE : Those values of the variable which do not satisfy the given equation but are obtained from the given equation

are known as extraneous roots of the given equation. Such a case arises when both sides of the equation are squared.
Example : Solve : $\small \sqrt{2x+9}+x = 13$
Solution : The given equation is $\small \sqrt{2x+9}+x = 13$ $\small \sqrt{2x+9} = 13-x$
Now,
       2x + 9 = (13 – x)²
           [On squaring both sides]
       x² – 28x + 160 = 0
       x² – 20x – 8x + 160 = 0
       x (x – 20) – 8 (x – 20) = 0
       (x – 20) (x – 8) = 0
       x – 20 = 0 or x – 8 = 0
       x = 20 or x = 8
   Clearly, we have to find those solutions for which
   2x + 9 0 and 13 – x 0
   i.e., x ³ – 9/2 and x <= 13
       Þ – 9/2 <= x <= 13
   Since x = 20 does not satisfy this condition. So, it is the extraneous root.
   Hence, x = 8 is the only root of the given equation.

Type 7 : Equations of the form
   , $\small \sqrt{^{ax2}+bx+c} = dx+e$
   where a, b, c, d, e R.
   Algorithm to solve equations of the form .

Step 1 : Obtain the equation. Let the equation be $\small \sqrt{^{ax2}+bx+c} = dx+e$
Step 2 : Square both sides of the equation in step 1 to obtain the quadratic equation ax² + bx + c = (dx + e)² or x² (a – d²) + x (b – 2 de) + (c – e²) = 0.
Step 3 : Solve the quadratic obtained in step 2.
Step 4 : Put ax² + bx + c 0 and dx + e 0 to obtain two inequations.
Step 5 : From the set of values obtained in step 3, take those values only which satisfy the inequations in step 4.

Other values are extraneous roots of the equation.
Step 6 : The values obtained in step 5 form the solution set of the equation.
Following examples illustrate the above algorithm.

Example : Solve :. $\small \sqrt{{3^{x2}+x+5} = x-3$
Solution : We have : $\small \sqrt{{3^{x2}+x+5} = x-3$
   3x² + x + 5 = (x – 3)2
   2x² + 7x – 4 = 0
   2x² + 8x – x – 4 = 0
   2x (x + 4) – (x + 4) = 0
   (2x – 1) (x + 4) = 0
   2x – 1 = 0 or x + 4 = 0
   x = 1/2 or x = – 4
   We have to find those solutions which satisfy the inequations
       3x² + x + 5 0 and x – 3 0.
   Clearly, none of these two values satisfy both the inequations
       3x² + x + 5 0 and x – 3 0
   Hence, the given equation has no solution.

Type 8 : Equations of the form
   $\small \sqrt{ax+b}+\sqrt{cx+d}=e$ or
      $\small \sqrt{ax+b}-\sqrt{cx+d}=e$
   where    a, b, c, d, e R.

* Algorithm :

Step 1 : Obtain the equation. Let the equation be $\small \sqrt{ax+b}\pm \sqrt{cx+d}=e$
Step 2 : Transfer one of the expressions with radical sign to the other side.
Step 3 : Square both sides and simplify in such a manner that the expression involving radical sign on one side and all other terms are on the other side.
Step 4 : Square both sides of the equation obtained in step 3 and simplify it to obtain a quadratic in x.
Step 5 : Solve the quadratic obtained in step 4.
Step 6 : Reject those values, obtained in step 5, which do not satisfy ax + b 0 and cx + d 0.
Step 7 : These values which satisfy the inequations in step 6 and the given equation determine the solution set of the given equation.
Following examples illustrate the above algorithm.

Example : Solve : $\small \sqrt{4-x} + \sqrt{x+9} = 5$
Solution : We have : $\small \sqrt{4-x} + \sqrt{x+9} = 5$
   $\small \sqrt{4-x} = 5- \sqrt{x+9}$
      $\small \left ( \sqrt{4-x} \right )^{2} = \left ( 5-\sqrt{x+9} \right )^{2}$             [On squaring both sides]
   4 – x = 25 + x + 9 – 10 $\small \sqrt{x+9}$
   – 2x – 30 = -10 $\small \sqrt{x+9}$
   (x + 15)² = 25 (x + 9)
   x² + 5x = 0
   x (x+ 5) = 0
   x = 0 or x = – 5
   We have to find those solutions for which 4 – x 0 and x + 9 0 i.e., x <= 4 and x 9 i.e.,
   – 9 <= x <= 4.
   Clearly, x = 0 and x = – 5 satisfy this condition and they also satisfy the given equation.
   Hence, the roots of the given equation are 0 and – 5.

·     Finding the roots of a quadratic equation by graphical method :
   Let us learn how to draw the graph of y = x²
   We assume certain real values for x, i.e., we substitute some values for x in y = x². We can find the corresponding values of y.

We tabulate the values, as shown below.

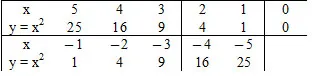
Plotting the points corresponding to the ordered pairs (5, 25), (4, 16), (3, 9), (2, 4), (1, 1), (0, 0), (– 1, 1), (– 2, 4), (– 3, 9),

(– 4, 16) and (– 5, 25) on the graph paper and joining them with a smooth curve we obtain the graph of y = x²,. as shown below.
We observe the following about the graph of y = x².
1. It is a U shaped graph and it is called a parabola. The arms of the ‘U’ spread outwards.
2. For every value of x (¹ 0) we notice that y is always positive. Hence, the graph lies entirely in the first and second quadrants.
3. When x = 0, y = 0 y = x2 passes through origin.
4. The graph is symmetric about the y-axis.
5. Using the graph of y = x2, we can find the square of any real number as well as the square root of any non-negative real number.

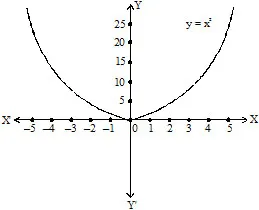
   (a) for any given x value, the corresponding y value on the graph is its square and
   (b) for any given y ( 0) value, the corresponding x value on the graph is its square root.
6.     The graph of y = kx², when k > 0 lies entirely in Q1 and Q2 and when k < 0 the graph lies entirely Q3 and Q4
   (i)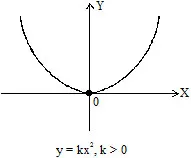

(ii)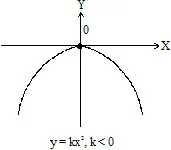
   The method of solving the quadratic equation of the form px2 + qx + r = 0 whose roots are real is shown in the following example.
Example Solve : 2x² – x – 3 = 0
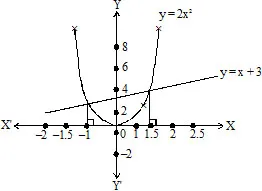
Solution : We know that the roots 2x² – x – 3 = 0 are the x coordinates of the points of intersection of the parabola y = 2x² and the line y = x + 3.
(1)   y = 2x²

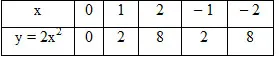
(2)   y = x + 3

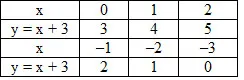
Draw the graph of y = 2x² and y = x + 3. Clearly, the perpendiculars drawn from the points of intersection of parabola and the

line meet the x-axis (3/2,0) at and (– 1, 0)
   \ The roots of the given quadratic equation 2x² – x – 3 = 0 are 3/2 and – 1.

Quadratic in Equations

   Consider the quadratic equations ax² + bx + c = 0, (a 0) where a, b and c are real numbers.
   The quadratic inequations related to ax² + bx + c = 0 are ax² + bx + c < 0 and ax² + bx + c > 0.
   Assume that a > 0.
   The following cases arise :

Case I
   If b² – 4ac > 0, then the equation ax² + bx + c = 0 has real and unequal roots.
   Let a and b (a < b) be the roots.
   Then,
   \ ax² + bx + c = a (x – a) (x – b)



   (a)     If x < a, then (x – a) < 0
       and    (x – b) < 0
   \     ax² + bx + c > 0
   (b)     If a < x < b, then (x – a) > 0
       and (x – b) < 0
   \     ax² + bx + c < 0
   (c)     If x > b, then x – a > 0
       and x – b > 0
   \     ax² + bx + c > 0

Case II
   If b² – 4ac = 0, then ax² + bx + c = 0 has real and equal roots.
   Let x' be the equal root.
   ax² + bx + c = a (x – x¢) (x – x¢)

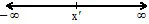
   (a)     If x < x'. Then x – x' < 0
   \    ax² + bx + c > 0
   (b)     If x > x', then x – x' > 0
   \    ax² + bx + c > 0

Case III
   If b2 – 4ac < 0, then ax² + bx + c = 0 has imaginary roots.
   In this case, ax² + bx + c > 0,
   The above concept can be summerised as
   (i)    If a < x < b, then (x – a) (x – b) < 0 and vice - versa.
   (ii)    If x < a or x > b (a < b), then (x – a) (x – b) > 0 and vice - versa.

   Note: If a < 0 and b² – 4ac < 0 then the solution for ax² + bx + c > 0 does not exist.
Example :
   Solve the inequation x² + x – 6 < 0.
Solution :
   Given inequation is x² + x – 6 < 0
      (x + 3) (x – 2) < 0
      (x + 3) < 0, (x – 2) > 0
   or     (x + 3) > 0, (x – 2) < 0
      x < –3, x > 2 (case I)
   (or)     x > –3, x < 2 (case II)
Case I
   x < –3, x > 2

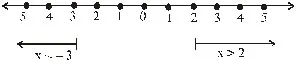
   There exist no value of x so that x < – 3 and x > 2 (as there is no overlap of the region).
   Hence in this case no value of x satisfies the given inequation.

Case II
x > –3, and x < 2

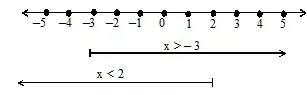
   All the points in the overlapping region, i.e., – 3 < x < 2, satisfy the inequation. Hence, the solution of the inequation
   x² + x – 6 < 0. is {x / –3 < x < 2} or ( –3, 2)
Example :
   Solve for x : x² – 4x + 3 ³ 0.
Solution :
   Given inequation is x² – 4x + 3 0.
   (x – 1) (x – 3) ³ 0
       x – 1 0; x – 3 0
   or     x – 1 <=0 0; x – 3 <=0
       x 1; x 3 (Case I) (or)
       x <= 1; x <= 3 (Case II)

Case I
   x 1 and x 3



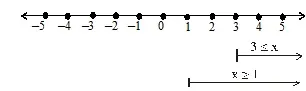
   All the points in the overlapping region, i.e., x ³ 3, satisfy the given inequation.
Case II
   x <= 1 and x <= 3




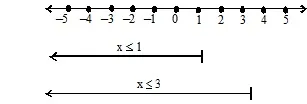
   All the points in the overlapping region, i.e., x <= 1, satisfy the given inequation
   Hence, the solution for the given inequation is
   x <= (– $\small \infty$ , 1] $\small \cup$ [3, $\small \infty$ )
Example-1
   Find the value of quadratic polynomial p(x) = 5x² – 6x + 3 at x = –1 and x = 3
Solution :
   p(x) = 5x² – 6x + 3
   p(–1) = 5(–1)² – 6(–1) + 3
   5 + 6 + 3 = 14
   p(3) = 5(3)² – 6(3) + 3
   5 × 9 – 18 + 3
   45 – 18 + 3 = 30
Example-2
   Check whether the following are quadratic equations.
   (a) (2x –1) (x – 3) = (x + 5) (x – 1)       (b) (x + 2)³ = 2x (x² – 1)
Solution :
(a)       (2x – 1) (x – 3)   = (x + 5) (x – 1)
       2x² – 6x – x + 3 = x² – x + 5x – 5
       2x² – 7x + 3 = x² + 4x – 5
       2x² – x² – 7x – 4x + 3 + 5 = 0
       x² – 11x + 8 = 0

It is of the form ax²+ bx + c = 0
Therefore, the given equation is a quadratic equation.

(b)   (x + 2)³ = 2x(x² – 1)
       x³ + 8 + 6x (x + 2) = 2x³ – 2x
       x³ + 8 + 6x² + 12x = 2x³ – 2x
       x³ – 2x³ + 6x² + 12x + 2x + 8 = 0
       –x³ + 6x² + 14x + 8 = 0
   or     x³ – 6x² – 14x – 8 = 0
   It is not of the form ax² + bx + c = 0 and it is not quadratic.
Example-3
   If 2 and – are the solutions of the quadratic equation 3x² = bx + c. Determine the value of b and c.
Solution :
   Since 2 and – 2/3 are solutions of the equation 3x² – bx – c = 0, then :
   Since 2 is root of 3x² – bx – c = 0, then :   3 (2)² – 2b – c = 0
   2b + c = 12       ......(1)
   – 2/3 is a root of 3x² – bx – c = 0, then :
   3(-2/3)² – b(-2/3) – c = 0
   3(4) – 2b – c = 0
   3 (4/9) + (2b/3) – c = 0
   –2b + 3c = 4   ....(2)
   Solving (1) and (2), we get
       12 = 2b + c       b = 4
       4 = –2b + 3c        c = 4
   Required values of b and c are 4 and 4 b = 4 = c

Example - 4
   If 4 is a root of the equation px² – 54x + 40 = 0, find the value of p and also find the other root.
Solution :
   The given equation is px² – 54x + 40 = 0 ..(i)
   Since 4 is a root of the equation (1) then we must have
   p(4)² – 54(4) + 40 = 0
   16p – 216 + 40 = 0
   16p – 176 = 0
   16p = 176 p = 176/16 = 11
(1)      f(x) = 11x² – 54x + 40 = 0 ..... (2)
   Since 4 is a root of f(x) then (x – 4) is a factor of f(x).
   Divide 11x² – 54x + 40 by (x – 4) then we get :
       f(x)    = 11x² – 54x + 40 = 0
           = (x –4) (11x – 10) = 0
   Either (x – 4) = 0 or 11x – 10 = 0
       x = 4 or x = 10/11
   Required value of p is 11 and other root is 10/11

Example - 5
   If the sum of the roots of ax²+ bx + c = 0 is equal to the sum of the squares of the roots then find the condition.
Solution :
   If a, b are the roots of ax² + bx + c = 0 then a + b = -b/a , a . b = c/a
   Given that a + b = a² + b²
       a + b = (a + b)² – 2a . b
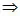-b/a = (-b/a)² – 2 . c/a = b²/a² – 2c/a
       -b/a = b²-2ac/a²
      -b/a × a² = b² – 2ac
       –ab = b² – 2ac
       2ac = b² + ab
       2ac = b² + abExample - 6
   If a and b are the roots of quadratic equations px² – qx + r = 0, form the equation whose roots are and
Solution :

Example - 7
   If one of the roots of the quadratic equation 2x² + px + 4 = 0 is 2, find the other root. Also, find the value of p.
Solution :
   The given equation is 2x² + px + 4 = 0.
   Here the product of the roots = = 2. Since, the one root of the equation = 2.
   Therefore the other root = 2/2 = 1 ....(i)
   Now the sum of the roots = – p/2.
   One of the roots of the equation is 2
   The other root = -p/2 – 2 = -p-4/2...(ii)
   From (i) and (ii), we have,
-p-4/2 = 1 –p – 4 = 2
       –p = 2 + 4 = 6
       p = –6.
   Hence, p = –6 and the other root = 1.

Example - 8
   Find the discriminant and the roots of the quadratic equation
       3x² – 5x + 2 = 0
Solution :
   In the equation 3x² – 5x + 2 = 0
   a = 3, b = –5, c = 2.
   D = b² – 4ac = 25 – 24 = 1 > 0.

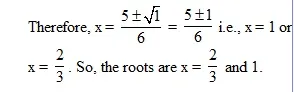
Example - 9
   Determine the nature of the roots of the following quadratic equation :
   x² – 4x + 4 = 0.
Solution :
   The given equation is x² – 4x + 4 = 0
   Here, a = 1, b = –4 and c = 4
   D = b² – 4ac = (–4)² – 4 × 1 × 4 = 0
   Since D = 0, therefore roots are real and equal.

Example - 10
   Find the values of k for which the given equation has real and equal roots.
Solution :
   2x² – 10x + k = 0
   a = 2, b = 10, c = k
   D = b² – 4ac = (–10)² – 4 × 2 × k = 0
   The given equation will have real and equal roots if
   D = 0 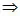100 – 8k = 0 k = 100/8 = 25/2

Example - 11   Find the condition that the quadratic equations x2 + ax + b = 0 and x2 + bx + a = 0 may have a common root.
Solution :
   Let a be a common root of the given equations.
   Then   a2 + aa + b = 0
   and   a2 + ba + a = 0
   By the method of cross-multiplication, we get
   = =
   This gives a2 = = –(a + b) and a = 1
   (1)2 = –(a + b) 1 = –a –b
   a + b + 1 = 0 is the required condition.

Example - 12
   Using factorisation solve the quadratic equation
       (x + 5)2 = 36
Solution :   The given quadratic equation is :
       Þ   (x + 5)2 – 36 = 0
       Þ   (x + 5)2 – (6)2 = 0       [Form : a2 – b2 = (a + b) (a – b)]
       Þ   (x + 5 + 6) (x + 5 – 6) = 0
       Þ   (x + 11) (x – 1) = 0
       Þ   Either x + 11 = 0 or x – 1 = 0
       Þ   x = –11 or x = 1
   Roots of the given equation are 1 and –11
Example - 13
   Find the root of the quadratic equation (if exist) by the method of completing the square.
       2x2 – 7x + 3 = 0
Solution :
       2x2 – 7x + 3 = 0
   Þ   2x2 – 7x = –3
   [Transpose the Constant to the other side]
   Þ   x2 – x = –
       [Divide both sides by 2]
   Þ   x2 – x + = –            [Make the LHS as perfect square]
   Þ   x2 – 2(x) + =            [From a2 – 2ab + b2 = (a – b)2]
   Þ   =
   Þ   =            [Taking square root of both sides]
       x = + =
       x = 3
   Þ   =
       [Taking both signs separately]
       x – =
       x = – =                x – =
       x =
       Required roots are 3 and
Example - 14
   Using quadratic formula, solve the equation :
   a2b2x2 – (4b4 – 3a4)x – 12a2b2 = 0
Solution :
   We have a2b2x2 – (4b4 –3a4)x – 12a2b2 = 0
   Here,   a = a2b2, b = –(4b4 – 3a4)
   and c = – 12a2b2
   Now, Discriminant,
   D = [–(4b4 – 3a4)]2 – 4 (a2b2) × (12a2b2)   [ D = b2 – 4ac]
       = 16b8 – 24a4b4 + 9a8 + 48 a4b4
       = 16b8 + 24a4b4 + 9a8
       = (4b4)2 + 2 × 4b4 × 3a4 + (3a4)2
       = (3a4 + 4b4)2
   Since D > 0, the given equation has two real and distinct roots, as
   x =
   =
   a =
   and b   =
   a =    and   b =
   a =    and   b=
   Hence, the roots of the equation are and

Example - 15
       Solve for y : 9y4 – 29y2 + 20 = 0
Solution :
       9y4 – 29y2 + 20 = 0
       Put y2 = x
       9x2 – 29x + 20 = 0
       9x2 – 20x – 9x + 20 = 0
       (x – 1)(9x – 20) = 0
      x = 0 or x =
       y2 =1 or y2 =
       y = ±1 and y = ±
·   px + = r.
       px2 – rx + q = 0
   and    p (x – a) + = r
      p (x – a)(x – b) – r (x – b) + q = 0

Example - 16
   Solve : 2x = 5
Solution :
   2x = 5
           2x2 – 3 = 5x
           (2x + 1) (x – 3) = 0
           x = or x = 3.
Example - 17

Solution :


= 0
   Either
   or

   Squaring on both sides
   x2 + 12x + 36 = 4 (x2 + x - 6)
   x = 6, x = –
   Since the equation involves radical therefore substituting x = 2, 6 and in the original equation,

we find that x = - does not satisfy the equation.
x = 2, 6

·   (i) x2a + xa + b = 0
   (ii) xa + x–a = b
   Put xa = y to get a quadratic equation in y. i. e., (i) y2 + y + b = 0 (ii) y + = b
Example - 18
   Solve for x :3 x + 2 + 3–x = 10
Solution:
   3 x + 2 + 3–x -10 = 10
   3x . 32 +
   Let 3x = y



   When y =
   x = – 2
   When y = 1
   = 1
   x = 0

Example - 19
   Find the whole number which when decreased by 20 is equal to 69 times the reciprocal of the number.
Solution :
   Let the given whole number be x where x > 0
   Condition I
   (x – 20) = 69    x(x–20) = 69
   x2 – 20x – 69 = 0
   x = =
   = = ;
   = 23, – 3 (rejected) x = 23
   x   = 23
   Required whole number is 23

Example - 20
The difference of squares of two natural numbers is 45. The square of the smaller number is four

times the larger number. Find the number.
Solution :
   Let the larger number be x and the smaller number be y
   From (1) and (2), we get :
   Condition I      x2 – y2 = 45 .......(1)
   Condition II       y2 = 4x   .......(2)       x2 – 4x = 45
   Putting these values of x in the equation (2) we get :       x2 – 4x – 45 = 0
   y2 = 4x when x = 9
   (x + 5) (x – 9) = 0 x = 9, –5
   y2 = 4 × 9 = 36 y = 6
   Required numbers are : 9, 6 or 9, –6
Example - 21
   The numerator of a fraction is one less than its denominator. If 3 is added to each of the numerator

and denominator, the fraction is increased by . Find the fraction.
Solution :
   Let the denominator of the required fraction be x
   Then the numerator of the fraction = x – 1
   Condition I
       Fraction= =                     ...(1)
   Condition II
       New Fraction =
       = = .....(2)
   Condition III
          = +
      – =
           =
      =
       x2 + 3x – 28 = 0
       x =    =       x = 4, –7 (rejected) x = 4
   When x = 4 then x – 1 = 3
   Required fraction = =
Example - 22
   The length of the hypotenuse of a right triangle exceeds the length of the base by 2 cm and exceeds twice the length of the altitude

by 1 cm. Find the length of each side of the triangle.
Solution :
Let the altitude (AB) of right.

   ABC be x cm. x > 0
   It is given that hypotenuse (AC) exceeds twice
   the length of the altitude (AB) by 1 cm
       AC = (2x + 1) cm; AB = x cm
   Also the hypotenuse (AC) exceeds the base (BC) by 2 cm
       BC = {(2x + 1) –2}m = (2x – 1)m
   Using Pythagorean Theorem in ABC, we have
   AC2 = AB2 + BC2 (2x + 1)2
   = x2 + (2x – 1)2
       (2x + 1)2 = x2 + (2x – 1)2
      4x2 + 4x + 1 = x2 + 4x2 – 4x + 1
       x2 – 8x = 0 x(x–8) = 0 x = 8       [ x > 0]
   Altitude = AB = x cm = 8 cm.
   Base = BC = (2x – 1) cm
   = (2 × 8 –1) cm = 15 cm
   Hypotenuse = AC = (2x +1) cm
       = (2 × 8 + 1) cm = 17 cm
   The length of the sides of right ABC are : 8 cm, 15 cm, 17 cm

Example - 23
An express train takes 1 hour less than a passenger train to travel 131 km between Mysore and Bangalore. If the average speed

of the express train is 11 km/hour more than that of the passenger train, find the average speed of the two trains.
Solution :
   Let the speed of passenger train = x km/hr, where x > 0
   Then the speed of express train = (x + 11) km/hr.
   t1 = Time taken by the passenger train to cover 132 km at speed x km/hr = hours
   t2 = Time taken by the express train to cover 132 km at speed (x + 11) km/hr = hours
   Condition
      – = 1
      132 = 1
       =
      =
      x2 + 11x – 1452 = 0
   x = = =
   x = 33, –44 (rejected)
   x = 33    [ x > 0]
   Required speed of the passenger train
   = 33 km/hr
   Speed of the express train = (33 +11) km/hr = 44 km/hr
   Verification t1 = = 4 hours
   and t2 = = 3 hours, t1 – t2 = 1 hour
Example - 24
   Two water taps together can fill a tank in hours. The tap of larger diameter takes 10 hours less than the smaller

one to fill the tank separately. Find the time in which each up can separately fill the tank.
Solution :
   Let the smaller tap take x hours to fill the tank, where (x Î N)
   then the larger tap take (x – 10) hours to fill the tank where x Î N
   Part filled by the smaller tap in one hour =
   Also the part filled by the larger tap in one hour =
   But the total time taken by both the taps to fill the tank = hours = hours.
   Part filled by both the taps in one hour =
       + =
       =
       150x –750 = 8x2 – 80x
       x =
       =
       x = = ; = 25,
       (rejected)
       x = 25 ( x Î N)
   Hence the smaller tap take 25 hours to fill the tank while the larger tap take (25 –10) = 15 hours to fill the tank.

1. Find the sum and the product of the roots of the equation x2 + 27x + 5 = 0.
(a) –9, 5 (b) 9, 5
(c) 6, –5 (d) 6, 5

2.   If a and b are the roots of the equation x2 – 12x + 32 = 0, then find the value of
(a) (b)     (c) (d)
3.   If the roots of the equation ax2 + bx + c = 0 are a and b, then the quadratic equation whose roots are –a and –b is
(a) ax2 – bx – c = 0 (b) ax2 – bx + c = 0
(c) ax2 – bx – c = 0 (d) ax2 – bx + 2c = 0
4.   Find the sum and the product of the roots of the quadratic equation –x2 – x + 25 = 0
(a) , 25 (b) , 25
(c) , –25 (d) , –25
5.   For what value of k is one root of the quadratic equation 9x2 – 18x + k = 0 double the other?
(a) 36 (b) 9 (c) 12 (d) 8
6.   If a and b are the zero of the quadratic polynomial ax2 + bx + c such that x does not lie between a and b, then
(a) a > 0 and ax2 + bx + c < 0 (b) ax2 + bx + c < 0 and a < 0
(c) a > 0 and ax2 + bx + c < 0 (d) Both (b) and (c)
7.   The condition for the sum and the product of the roots of the quadratic equation ax2 – bx + c = 0 to be equal, is
(a) b + c = 0 (b) b – c = 0
  (c) a + c = 0 (d) a + b + c = 0
8.   Which of the following are the roots of the equation + – 6 = 0?
(i) 2 (ii) –2   (iii) 3 (iv) –3
(a) Both (i) and (ii) (b) Both (iii) and (iv)
(c) (i), (ii), (iii) and (iv) (d) None of the above
9.   If the roots of the quadratic equation ax2 + bx + c = 0 are a and b, then the equation whose roots are a2 and b2 is
(a) a2x2 – (b2 – 2ac)x + c2 = 0 (b) a2x2 – b2x + c2 = 0
(c) a2x2 + (b2 + 2ac)x + c2 = 0 (d) a2x2 – (b2 + 2ac)x + c2 = 0
10.  If the roots of the equation3ax2 + 2bx + c = 0 are in the ratio 2 : 3, then
(a) 8ac = 25b
   (b) 8ac = 9b2
(c) 8b2 = 9ac
(d) 8b2 = 25 ac
11.  Find the roots of the equation l2 (m2 – n2) x2 + m2 (n2 – l2)x + n2 (l2 – m2) = 0.
(a) 1,
(b) 1,
(c) 1,
(d) 1,

12.   If a – b, b – c are the roots of ax2 + bx + c = 0, then find the value of .
(a) (b) (c) (d)
13.   If the roots of the equation 2x2 + 7x + 4 = 0 are in the ratio p : q, then find the value of + .
(a) ± (b) ± 7
  (c) ± (d) ±
14.   If one root of x2 + px + 12 = 0 is 4, while the equation x2 + px + q = 0 has equal roots, then the value of q is–
(a) 49/4        (b) 4/49
(c) 4 (d) 1/4
15.   One root of x2 + kx – 8 = 0 is square of the other, then the value of k is:
(a) 2   (b) 8 (c) – 8 (d) –2
16.   Given the quadratic equation x2 – (A – 3) x – (A –2), for what value of A will the sum of the squares of the roots be zero
(a) –2 (b) 3
(c) 6 (d) None of these
17. If the roots, x1 and x2 of the quadratic equation x2 – 2x + c = 0 also satisfy the equation 7x2 –4x1 = 47, then which of the following is true –
(a) c = –15
(b) x1 = – 5, x2 = 3
(c) x1 = 4.5, x2 = –2.5
(d) None of these
18.  If a and b are the roots of the equation ax2 + bx + c = 0), then what is the value of (a2 + b2)– I. a + b = –II. 2ab =
(a) 1          (b) 2
(c) 3 (d) 4
19. If the sum of the roots of the quadratic equation ax2 + bx + c = 0 is equal to the sum of the squares of their reciprocals, then c/a, a/b, b/c are in
(a) A.P.           (b) G.P.
(c) H.P.           (d) None of these
20. If the roots of x2 – bx + c = 0 are two consecutive integers, then b2 – 4c is–
(a) 1          (b) 2
(c) 3 (d) 4
21 . If a ¹ b but a2 = 5a – 3 and b2 = 5b – 3, then the equation whose roots are a/b and b/a is-
(a) 3x2 – 25 x + 3 = 0
(b) x2 + 5x – 3 = 0
(c) x2 – 5x + 3 = 0
(d) 3x2 – 19x + 3 = 0
22.   Quadratic equation whose one of the roots is is :
(a) x2 + 8 x – 1 = 0               (b) x2 + 8 x + 18 = 0
(c) x2 –8 x + 1 = 0 (d) x2 – 8 x + 11 = 0
23. If a root of x2 – k x + 8 = 0 is 4, then k = ______
  (a) 7           (b) 3           (c) 6           (d) 8
24. If (x+1) is a factor of 3x2 +k x + 4,hen k = ______
(a) 3           (b) 6           (c) –7           (d) 7
25.   If x2 –2px + 8p – 15 = 0 has equal roots, then p = ______
(a) 3 or –5       (b) 3 or 5       (c) –3 or 5       (d) –3 or –5
26.   Find the nature of the roots of the equation 4x2 – 2x – 1 = 0
(a) Real and equal (b) Rational and unequal
(c) Irrational and unequal (d) Imaginary
27.   If the quadratic equation (a2 – b2) x2 +(b2 – c2)x + (c2 – a2) = 0 has equal roots, then which of the following is true ?
(a) b2 + c2 = a2
(b) b2 + c2 = 2a2
(c) b2 – c2 = 2a2
(d) a2 = b2 + 2c2
28.   The roots of the quadratic equation 2x2 + 3x + 1 = 0 are
(a) Irrational
    (b) Rational
(c) Imaginary
(d) None of these
29.   If roots of the given equation (cos p – 1) x2 + (cos p) x + sin p = 0 are real , then –
(a) p Î (–p, 0)        (b) p Î    (c) p Î (0, p)       (d) p Î (0, 2p)

30. If the discriminant of 3x2 –14 x + k = 0 is 100, then k = ______
(a) 8 (b) 32 (c) 16 (d) 24

31.   The roots of x2 – x + 1 = 0 are :
   (a) Real and Equal
(b) Real and not equal
(c) Imaginary
(d) Reciprocals

32.   The roots of the equation (x – a)(x – b) = b2 are :
(a) Real and equal
(b) Real and unequal
(c) Imaginary
(d) Equal
33.   The discriminant of ax2 – a(a + b)x + b = 0 is :
(a) a – b       (b) a + b (c) (a + b)2       (d) (a – b)2

34. The discriminant (d) of = 2 is :
(a) –3 (b) 13 (c) 11 (d) 12

35. The number of real roots of the equation , where A and B are real numbers not equal to zero simultaneously is:
(a) none (b) 1 (c) 2 (d) 1 or 2

36.   For what values of ‘k’ does the equation (k–2)x2 +2(2k–3)x + (5k–6) = 0 have equal roots?
Find the roots of the equations corresponding to those values of k?
(a) k = 1, Roots are –1, –1           (b) k = 1, Roots are 1, –1
k = 3, Roots are –3, –3           k = 3, Roots are 3, 3
(c) k = –1, Roots are –1, 1           (d) k = 1, Roots are 1, 1
  k = 3, Roots are 3, –3 k = 3, – 3
37.   If both ‘a’ and ‘b’ belong to the set {1, 2, 3, 4} then the number of equations of the form ax2 +bx+1 = 0 having real roots is :
(a) 10           (b) 7           (c) 6           (d) 12
38.   Which of the following equations has real roots?
(a) 3x2 +4x + 5 = 0 (b) x2 +x + 4 = 0 (c) (x – 1) (2x – 5) = 0 (d) 2x2 –3x + 4 = 0
39.   If both the roots of the quadratic equation x2 – 2kx + k2 + k – 5 = 0 are less than 5, then k lies in the interval ________
(a) (5,6]       (b) (6,)       (c) (–,4)       (d) [4,5]
40.   Find the values of c for which
x2 – 4 – 2x = c(x –4) has equal roots.
(a) c = 2 or 10       (b) c = 3 or 9       (c) c = 1 or 8       (d) c = 4 or 7
41.   If equation x2– (2 + m)x + 1(m2 – 4m + 4) = 0 has coincident roots, then :
(a) m = 0       (b) m = 6       (c) m = 2       (d) m =
42.   If 3.22x+1 – 5.2x+2 + 16 = 0 and x is an integer, find the value of x.
(a) 1 (b) 2
(c) 3    (d) 4
43.   If (x + 1) (x + 3) (x + 5) (x + 7) = 5760, find the real values of x.
(a) 5, –13 (b) –5, 13
(c) –5, –13 (d) 5, 13
44.   The roots of x2/3 + x1/3 – 2 = 0 are :
(a) 1 or –8       (b) 1 or –2       (c)        (d) –2 or –8
45.   The value of ‘x’ in the equation is :
(a) 5/13       (b) 7/13       (c) 9/13       (d) None of these
46.   The solutions for the equation are
(a) x = 1 or 2       (b)        (c) x = 0 or        (d) x = or 2
47.   Solve x2 – = 7
(a) –7           (b) ±3
(c) 7 (d)14
48.   If (7+)x + (7–)x = 128 then x is
(a) > 3           (b) Any value
(c) 4 (d) ±2
49.   The roots of the equation 3x – 4 – 4 = 0 are
(a) 2,        (b) , 2
(c) 4,        (d) 4,
50.   If y = x + then x4+x3-4x2+x+1 = 0 becomes
(a) x2(y2+y-6) = 0 (b) x2(y2+y-2) = 0
(c) x2(y2+y-3) = 0 (d) x2(y2+y-4) = 0
51.   If , then 4x equals
(a) 4 (b) 0
(c) 5          (d)

52.   The roots of
= 0 are
(a) 2 only        (b) only
(c) 2 or (d) none
53.   The roots of the equation 4x – 3.2x+2 + 32 = 0 would include
(a) 1, 2 and 3       (b) 1 and 2       (c) 1 and 3       (d) 2 and 3
54.   The value of x in the equation = 4 is
(a) –2           (b)            (c) – 1           (d) 0
55.   The value of x in the equation is
(a) 5/13       (b) 7/13       (c) 9/13       (d) None of these
56.   If (x - a ) /(b + c) +(x -b) / (c + a) + (x - c) /(a + b) = 3, then x is
(a) 0            (b) 1           (c) a + b + c        (d) abc
57.   The product of the solution of the equation, 4(22x)-33(2x)+8=0, is
(a) 2 (b) -3/4
(c) -6           (d) 1
58.   Number of solutions of the equation =x2 -4, is
(a) 0          (b) 1
(c) 2           (d) 4
59   Solution of 22x – 3.2x + 2 + 32 = 0 are :
(a) {3, 2}       (b) {–3, 2}
(c) {2, –3}       (d) {–3, –2}
60.   Solution set of 5(x + 1) + 5(2 – x) = 53 + 1 is
(a) [3, 4]       (b) [2, 1]        (c) [2, –1]        (d) [ 5, 2]
61.   The graph of y = 2x2 is :
(a) a straight line (b) a circle
(c) a parabola (d) None
62.   The polynomial x3 – 3x2 – 9x + c = 0 can be written in the form (x – a)2(x – b) if value of c is
(a) 5 (b) –7
  (c) 25            (d) 27
63.   The value of ‘k’ for which the quadratic equation 5x2 + 6(a2 + 2)x + (a2 – 5a + 6) = 0, possesses roots of opposite sign lies in
(a) (–2, –3)       (b) (2, 3)
(c) 5, 1           (d)

Direction (Q.64-68) Comment upon the values of a, b, c, D for standard Q.E. as y = ax2 + bx + c and find the correct statement

64. In the given figure

(a) a < 0        (b) b > 0
    (c) D > 0         (d) a > 0
65.   In the given figure

   (a) a < 0        (b) b > 0
   (c) D > 0         (d) a > 0

66.   In the given figure

   (a) a < 0        (b) b > 0
   (c) D > 0         (d) a > 0
67.   In the given figure

   (a) a < 0        (b) b > 0
   (c) D > 0         (d) a > 0
68.   In the given figure

   (a) a < 0        (b) b > 0
    (c) D > 0         (d) a > 0

Direction (Q.69-72) Find the inter-relationship in variables for the standard Q.E as y = ax2 + bx + x

69.   In the given figure

   (a) a = 0       (b) b = 0
   (c) c = 0       (d) D > 0
70.   In the given figure

   (a) a + b + c=0       (b) a - b + c=0
   (c) 2a+b+c=0       (d) 4a - 2b +c=0
71.   In the given figure

   (a) 9a - 3b + c = 0
   (b) 9a + 3b + c = 0
   (c) a+b+c=0
   (d) None
72.   In the given figure

   (a) a = 0 (b) a + c = 0
   (c) a - b - c = 0 (d) None

CBSE 10th CLASS MATHS CHAPTER QUADRATIC EQUATIONS

Standard form of Quadratic Equations

Recent Posts