A linear equation (or a first-degree equation) in two variables has both its variables raised to the first power only.
A linear equation in two variables is of the form ax + by + c = 0
where at least one of a, b is different from zero.
Note that 2x + 3 = 0 can be treated as a linear equation in two variables since we can rewrite it as 2x + 0y + 3 = 0.
Solution of a linear equation in two variables is a pair of values, one for x and the other for y which when substituted
in the given equation, make the two sides of the equation equal.
* Algebraic Methods of solving linear equations in two variables :
The most commonly used algebraic methods of solving linear equations in two variables are :
(i) Method of substitution.
(ii) Method of elimination by equating the coefficients
(iii) Method of cross-multiplication
* Method of Substitution:
In this method, we express one of the variables in terms of the other variable from either of the two equations and then
this expression is put in the other equation to obtain an equation in one variable as explained in the following algorithm.
Algorithm
Step:1 Obtain the two equations. Let the equations be
a1x + b1y +c1 = 0 ............ (i)
and a2x + b2y + c2 = 0 ...........(ii)
Step:2 Choose either of the two equations, say (i), and the other value of one variable, say y, in terms of the other, i.e. x.
Step:3 Substitute the value of y, obtained in step 2, in the other equation i.e. (ii) to get an equation in x.
Step:4 Solve the equation obtained in step 3 to get the value of x.
Step:5 Substitute the value of x obtained in step 4 in the expression for y in terms of x obtained in step 2 to get value of y.
Step:6 The values of x and y obtained in steps 4 and 5 respectively constitute the solution of the given system of two linear equations.
Following solved examples will illustrate the above algorithm.
Ex. Solve the following system of equation by using the method of substitution :
3x – 5y = –1, x – y = –1
Sol. The given system of equation is
3x – 5y = –1 .............(i)
x – y = –1 .............(ii)
From (ii), we get
y = x + 1
Substituting y = x + 1 in (i), we get
3x – 5(x + 1) = –1
=> –2x – 5 = –1
=> –2x = 4 Þ x = –2
Putting x = – 2 in y = x + 1 we get y = –1.
Hence, the solution of the given system of equation is x = –2, y = –1.
* Method of Elimination by equating the coefficients :
In this method, we eliminate one of the two variables to obtain an equation in one variable which can easily be solved.
Putting the value of this variable in any one of the given equations, the value of the other variable can be obtained.
Following algorithm explains the procedure.
Algorithm
Step:1 Obtain the two equations.
Step:2 Multiply the equations so as to make the coefficients of the variable to be eliminated equal.
Step:3 Add or subtract the equations obtained in step 2 according as the terms having the same coefficients are of opposite of the same sign.
Step:4 Solve equation in one variable in step 3.
Step:5 Substitute the value found in step 4 in any of the given equations and find the value of the other variable.
The value of the variables in step 4 and 5 constitute the solution of the given system of equations.
Ex.1 Solve the following system of linear equations by using the method of elimination by equating the coefficients :
3x + 2y = 11, 2x + 3y = 4
Sol. The given systems of equations is
3x + 2y = 11 ............(i)
2x + 3y = 4 ............(ii)
Let us eliminate y from the given equations. The coefficients of y in the given equations are 2 and 3 respectively. The L.C.M. of
2 and 3 is 6. So, we make the coefficients of y equal to 6 in the two equations.
Multiplying (i) by 3 and (ii) by 2, we get
9x + 6y = 33 ..............(iii)
4x + 6y = 8 ..............(iv)
Subtracting (iv) from (iii), we get
5x = 25 Þ x = 5
Substituting x = 5 equation in (i), we get
15 + 2y = 11Þ 2y = –4 Þ y = –2
Ex.2 Solve the following system of equations :

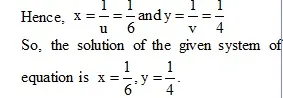
* Method of Cross-Multiplication :
Theorem : Let a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
be a system of simultaneous linear equations in two variables x and y such that
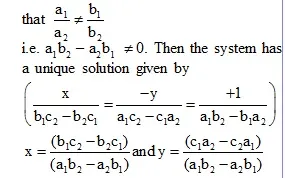
Ex. Solve the following systems of equations by using the method of cross-multiplication :
x + y = 7, 5x + 12y = 7
Sol. The given system of equation is
x + y – 7 = 0
5x + 12y – 7 = 0
By cross-multiplication, we get
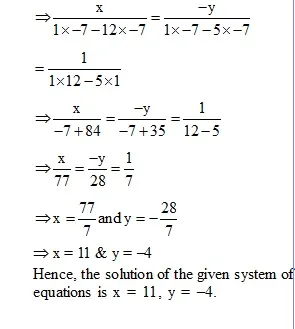
* Conditions for Consistency :
The system of equations
a1x + b1y + c1 = 0 .........(1)
a2x + b2y + c2 = 0 ........(2)
(i) is consistent with unique solution, if
![]()
i.e., lines represented by equations (1) and (2) are not parallel
(ii) is consistent with infinitely many solutions,
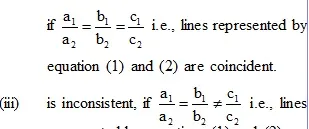
represented by equations (1) and (2) are parallel and non-coincident.
Ex. In each of the following systems of equations determine whether the system has a unique solution, no solution or
infinitely many solutions. In case there is a unique solution, find it :
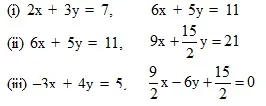
Sol. (i) The given system of equations may be written as
2x + 3y – 7 = 0
6x + 5y – 11 = 0
The given system of equations is of the form
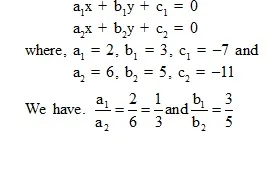
Clearly,
So, the given system of equations has a unique solution.
To find the solution, we use the cross- multiplication method.
By cross-multiplication, we have
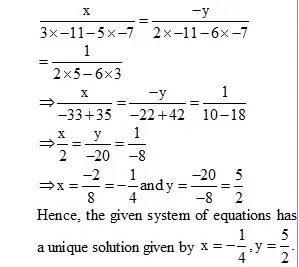
(ii) The given system of equations may be written as
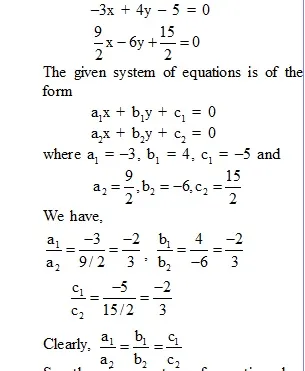
So, the given system of equations has infinitely many solutions.
Ex. Find the value (s) of k for which the system of equations
kx – y = 2
6x – 2y = 3
has (i) a unique solution (ii) no solution.
Is there a value of k for which the system has infinitely many solutions ?
Sol. The given system of equation is
kx –y – 2 = 0
6x – 2y –3 = 0
It is of the form a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
where a1 = k, b1 = –1, c1 = –2 and
a2 = 6, b2 = –2, c2 = –3
(i) The given system will have a unique solution, if
i.e., if ![]()
So, the given of equations system will have a unique solution, if
So, the given of equations system will have a unique solution , if
(ii) The given system will have no solution, if
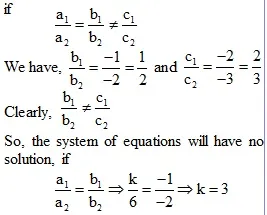
Hence, the given system will have no solution, if k = 3.
For the given system to have infinite number of solutions, we must have
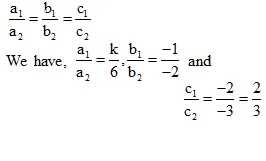
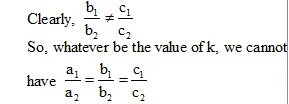
So, whatever be the value of k, we cannot have
Hence, there is no value of k, for which the given system of equations has infinitely many solutions.
Ex. For what value of k will the following system of linear equations has no solution?
3x + y = 1
(2k –1)x + (k –1)y = 2k + 1
Sol. We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
has no solution, if
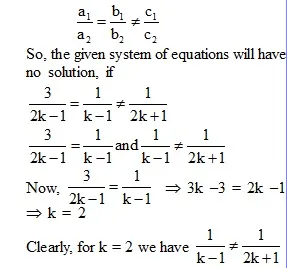
So, the given system of equations will have no solution, if
Hence, the given system of equations will have no solution, if k = 2.
Ex. I am three times as old as my son. Five years later, I shall be two and a half times as old as my son. How old am I and how old is my son ?
Sol. Suppose my age is x years and my son’s age is y years. Then,
x = 3y ............(i)
Five years later, my age will be (x + 5) years and my son’s age will be (y + 5) years.
\ x+5 = 5/2(y+5) (Given)
=> 2x – 5y – 15 = 0 ........ (ii)
Putting x = 3y in equation (ii), we get
6y – 5y – 15 = 0 Þ y = 15
Putting y = 15 in equation (i), we get
x = 45
Hence, my present age is 45 years and my son’s present age is 15 years.
1. How many pairs of x and y satisfy the equations 2x + 4y = 8 and 6x + 12 y = 24 ?
(a) 0 (b) 1
(c) Infinite (d) none of these
2. Find the value of ‘k’for which the system of linear equations kx + 2y = 5 and 3x + y = 1 has zero solutions.
(a) k = 6 (b) k = 3
(c) k = 4 (d) none of these
3. The total cost of 10 erasers and 5 sharpeners is at least Rs 65. The cost of each eraser cannot exceed Rs 4.
Find the minimum possible cost of each sharpener.
(a) Rs 6 (b) Rs 5.50
(c) Rs 5 (d) Rs 6.50
4. If the system of linear equations px + 3y = 9 and 4x + py = 8 has unique solution, then
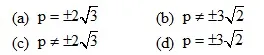
5. In a group of goats and hens, the total number of legs is 12 more than twice the total number of heads. The number of goats is :
(a) 8 (b) 6 (c) 2 (d) 10
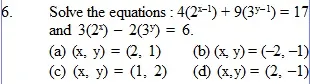
7. If (a + b, a –b) is the solution of the equations 3x + 2y = 20 and 4x –5y = 42, then find the value of b.
(a) 8 (b) – 2
(c) – 4 (d) 5
8. In a fraction, if numerator is increased by 2 and denominator is increased by 3, it becomes and if numerator
is decreased by 3 and denominator is decreased by 6, it becomes . Find the sum of the numerator and denominator.
(a) 16 (b) 18 (c) 20 (d) 14
9. If 100 cm is divided into two parts such that the sum of 2 times the smaller part and of the larger part, is less than
100 cm, then which of the following is correct ?
(a) Larger portion is always less than 60.
(b) Smaller portion is always less than 60 and more than 40.
(c) Larger portion is always greater than 60.
(d) Smaller portion is always greater than 40.
10. The fare of 3 full tickets and 2 half tickets is Rs 204 and the fare of 2 full tickets and 2 half tickets is Rs. 186.
Find the fare of a full ticket and a half ticket.
(a) Rs 94 (b) Rs 78
(c) Rs 86 (d) Rs 62
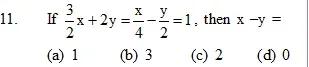
12. If we add 1 to the numerator and subract 1 from the denominator a fraction becomes 1. It also becomes if we add 1
to the denominator. Then the sum of the numerataor and denominator of the fraction is
(a) 7 (b) 8 (c) 2 (d) 11
13. If 4x – 3y = 7xy and 3x + 2y = 18xy, then (x, y) =
(a) (b) (3, 4)
(c) (4, 3) (d)
14. If 2 |x| – |y| = 3 and 4 |x| |+ |y| = 3, then number of possible order pairs of the form (x, y) is
(a) 0 (b) 1
(c) 2 (d) 4
15. A father wants to divide Rs 200 into two parts between two sons such that by adding three times the smaller part to half
of the larger part, then its will always be less than Rs 200. How will he divided this amount ?
(a) Smaller part is always less than 50
(b) Larger part is always greater than 160
(c) Larger part is always less than 160
(d) Smaller part is always greater than 40
16. A bus conductor gets a total of 220 coins of 25 paise, 50 paise and Re. 1 daily. One day he gets Rs 110 and next day he gets
Rs 80 in that the number of coins of 25 paise and 50 paise coins are interchanged then find the total number of 50 paise coins
and 25 paise coins.
(a) 180 (b) 190
(c) 160 (d) 200
17. An examination consists of 160 questions. One mark is given for every correct option. If one-fourth mark is deducted for
every wrong option and half mark is deducted for every question left, then one person scores 79. And if half mark is deducted
for every wrong option and one-fourth mark is deducted for every left question, the person scores 76, then find the number of
questions he attempted correctly.
(a) 80 (b) 100
(c) 120 (d) 140
18. The number of ordered pairs of different prime numbers whose sum is not exceeding 26 and difference between second number
and first number cannot be less than 10.
(a) 8 (b) 9
(c) 10 (d) 11
19. The number of possible pairs of succesive prime numbers such that each of them is greater than 40 and their sum is atmost 100 is
(a) 3 (b) 2
(c) 4 (d) 1
20. In an election the supporters of two candidates A and B were taken to polling both in two different vehicles, capable of carrying
10 and 15 voters respectively. If atleast 90 vehicles were required to carry a total of 1200 voters, then find the maximum number
of votes by which the elections could be won by the candidates, B.
(a) 900 (b) 600
(c) 300 (d) 500