Algebra is that branch of Mathematics in which letters represent any value which we can assign according to our requirement. These letters are generally of two types : constants and variables (or literal numbers).
* Constant :
A number having a fixed numerical value is called a constant.
Ex. 7,8/3,4,7,16.5 etc
* Variable :
A number which can take various numerical values is known as variable.
Ex. x, y, z, a, b, c, etc.
* Algebraic expression :
A combination of constants and variables connected by +, –, × and ¸ signs is known as an algebraic expression.
Ex. 8x + 7, 11x2 – 13x, 5x5 + 8x2y, etc.
* Terms :
The parts of an algebraic expression separated by + or – signs are called the terms of the expression.
Ex. In the expression 3x + 4y –7, we call 3x, 4y and –7 as terms.
* Coefficient of a term :
Consider the term 8x2. In this case, 8 is called the numerical coefficient and x2 is said to be the literal coefficient.
In case of 9xy, we have the numerical coefficient as 9 and the literal coefficient as xy.
* Like terms :
Terms having the same literal coefficients are called like terms.
Ex. 8x2y, 5x2y and –7x2y are all like terms.
* Unlike terms :
Terms having different literal coefficients are called unlike terms.
Ex. 5x2,–10x and 15x3 are unlike terms.
* Polynomial :
An algebraic expression in which the variables involved have only non-negative integral powers is called a polynomial.
Let x be a variable, n be a positive integer and a1, a2,....., an be constants (real numbers). Then,
f(x) = anxn + an – 1xn – 1 +.....+ a1x + a0
is called a polynomial in variable x.
In the polynomial,
f(x) = anxn + an – 1xn – 1 +.....+ a1x + a0,
anxn, an – 1xn – 1,..., a1x and a0 are known as the terms of the polynomial and an, an – 1, an – 2, ...., a1 and a0 are called their coefficients.
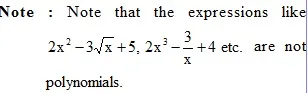
* Degree of a Polynomial :
The exponent of the highest term in a polynomial is known as its degree.
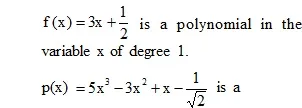
polynomial in the variable x of degree 3.
* Types of polynomials with respect to degree :.
1. Constant Polynomial :
A polynomial of degree zero is called a constant polynomial.
Ex. : f(x)=7,g(x) = -3/2 etc. are constant polynomial.
2. Zero Polynomial :
The constant polynomial 0 or f(x) = 0 is called the zero polynomial
Note : The degree of the zero polynomial is not defined, because
f(x) = 0, g(x) = 0x, h(x) = 0x2, p(x) = 0x3, q(x) = 0x12 etc. are all equal to the zero
3. Linear Polynomial :
A polynomial of degree 1 is called a linear polynomial.
Generally, any linear polynomial in variable x with real coefficients is of the form f(x) = ax + b, where a, b are real numbers and a != 0.
Ex. 11x – 5, 10y + 7
4. Quadratic Polynomial :
Polynomial of degree 2 is called a quadratic polynomial.
Ex. 5x2 – 8x + 3
5. Cubic Polynomial :
A polynomial of degree 3 is called a cubic polynomial.
Ex. 5x3– 6x2 + 7x + 8
6. Bi-Quadratic Polynomial :
A fourth polynomial is called a biquadratic polynomial.
Ex. 3x4 – x3 + 7x2 –2x + 1
* Types of polynomials with respect to number of terms :
1) Monomial : An expression containing only one term is called a monomial.
Ex. 8x, –11x2y, –15x2y332, etc.
2) Binomial : An expression containing two terms is called a binomial.
Ex. 3x – 8y, 4xy – 5x, 9x + 5x2, etc.
3) Trinomial : An expression containing three terms is called a trinomial.
Ex. 5x –2y + 3z, x2 + 2xy – 5z.,
* Relation between the HCF, the LCM and the product of polynomials :
If f(x) and g(x) are two polynomials then we have the relation,
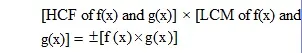
* Zero of a Polynomial :
A real number a is a zero of a polynomial f(x), if f(a) = 0.
Finding a zero of a polynomial f(x) means solving the polynomial equation f(x) = 0.
Geometrical Meaning of the Zeros of a polynomial :
Geometrically zeros of a polynomial are the x-coordinates of the points where its graph crosses or touches X-axis.
An nth degree polynomial can have at most n real zeros.
* Relationship Between the Zeros and Coefficient of a quadratic polynomial :
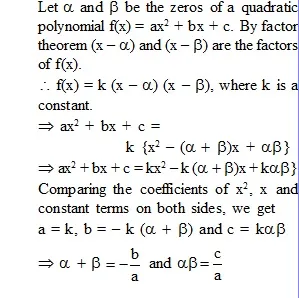

Example :

Example :
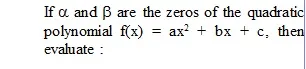

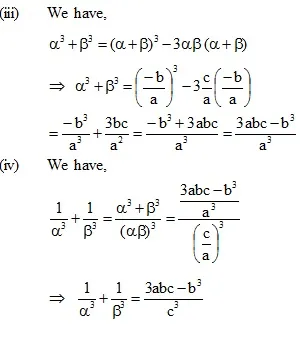
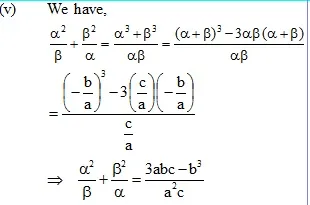
Example :
If sum of the squares of zeros of the quadratic polynomial f(x) = x2 – 8x + k is 40, find the value of k.

* Relationship between zeros and Coefficients of a Cubic polynomial :
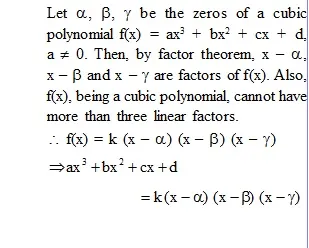
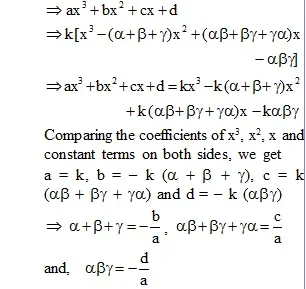

 s
s

Example :
Find the zeros of the polynomial
f(x) = x3 – 5x2 – 16x + 80, if its two zeros are equal in magnitude but opposite in sign.

![]()
Hence, the zeros are 4, – 4 and 5.
Division Algorithm for Polynomials :
Dividend = Quotient × Divisor +Remainder
This is known as Euclid’s division lemma the division of polynomials also follows the similar rule which is known as the division algorithm for polynomials.
Example :
Divide the polynomial
f(x) = 6x3 + 11x2 – 39x – 65 by the polynomial g(x) = x2 – 1 + x. Also, find the quotient and remainder.
Sol. We have,
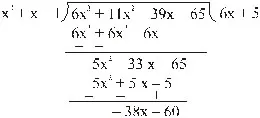
Clearly, quotient q(x) = 6x + 5 and remainder r(x) = – 38x – 60.
Also, 6x3 + 11x2 – 39x – 65
= (x2 + x – 1) (6x + 5) + (– 38x – 60)
i.e., f(x) = g(x) q(x) + r(x)
or, Dividend = Quotient × Divisor + Remainder
* Division Algorithm :
If f(x) and g(x) are any two polynomial with g(x) ¹ 0, then we can always find polynomials q(x) and r(x) such that
f(x) = q(x) g(x) + r(x), where r(x) = 0 or degree r(x) < degree g(x).
If r(x) = 0, then polynomial g(x) is a factor of polynomial f(x).
Example :
Obtain all the zeros of the polynomial f(x) = 3x4 + 6x3 – 2x3 – 2x2 – 10x – 5,
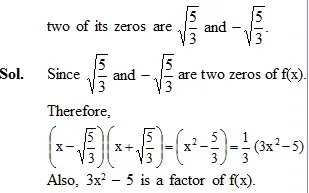
Let us now divide f(x) by 3x2 – 5.
We have,
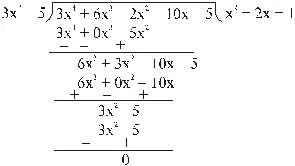

Example :
What must be subtracted from
8x4 + 14x3 – 2x2 + 7x – 8 so that the resulting polynomial is exactly divisible by 4x2 + 3x – 2.
Sol. We know that,
Dividend= Quotient × Divisor + Remainder
=> Dividend – Remainder = Quotient ×
Divisor
Clearly, RHS of the above result is divisible by the divisor.
Therefore, LHS is also divisible by the divisor. Thus, if we subtract remainder from the dividend, then it will be exactly divisible by the divisor.
Dividing 8x4 + 14x3 – 2x2 + 7x – 8 by 4x2 + 3x – 2, we get
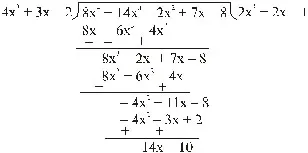
=> Quotient = 2x2 + 2x – 1 and Remainder = 14x – 10
Thus, if we subtract the remainder 14x – 10 from 8x4 + 14x3 – 2x2 + 7x – 8, it will be divisible by 4x2 + 3x – 2.
Example :If x4 + x3 + 8x2 + ax + b is exactly divisible by x2 + 1, then find the value of a and b.
Sol. If x4 + x3 + 8x2 + ax + b is exactly divisible by x2 + 1, then the remainder should be zero.
On dividing, we get
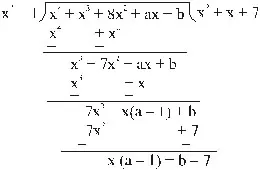
=> Quotient = x2 + x + 7 and Remainder = x (a – 1) + (b – 7)
Now,
Remainder = 0
=> x (a – 1) + (b – 7) = 0
=> x (a – 1) + (b – 7) = 0x + 0
=> a – 1 = 0 and b – 7 = 0
=> a = 1 and b = 7*
* Factorisation of A3 + B3 + C3 –3ABC

* Homogeneous expression :
An algebraic expression in which, the degree of all the terms are equal is a homogenous expression.
e.g. bx + ay is a first degree homogenous expression, ax2 + bxy + cy2 is a second degree homogenous expression.
Note : The product of two homogeneous expressions is a homogeneous expression.
* Symmetric expressions :
f(x, y) is an expression in variables x and y.
If f(x, y) = f(y, x), then f(x, y), is called a symmetric expression.
i.e., If an expression remains same after interchanging the variables x and y is said to be a symmetric expression.
Example :
Consider the expressions
(i) ax + ay + b
(ii) ax2 + bxy + ay2
(i) Let f(x, y) = ax+ ay + b
f(y, x) = ay + ax + b
= ax + ay + b
=> f(y, x) = f(x, y)
ax + ay + b is symmetric.
(ii) f(x, y) = ax2 + bxy + ay2
f(y, x) = ay2 + byx + ax2
= ay2 + bxy + ax2
= ax2 + bxy + ay2
=> f(y, x) = f(x, y)
=>Hence, ax2 + bxy + ay2 is symmetric.
Note : An expression which is homogeneous and symmetric is called a homogenous symmetric expression.
Ex. ax + ay, ax2 + bxy + ay2.
* Cyclic Expressions :
f(x, y, z) is an expression in variable x, y and z.
If f(x, y, z) = f(y, z, x) then f(x, y, z) is cyclic.
Example :
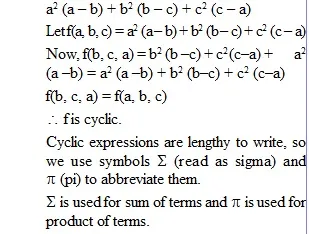
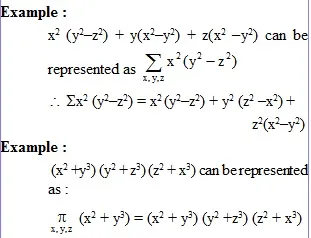
* Remainder Theorem :
When a polynomial p(x) in x is divided by (x – a), the remainder is equal to the value of the polynomial p(x) at x = a, i.e., equal to p(a).
* Factor Theorem :
The binomial (x–a) is a factor of a polynomial p(x) in x if and only if the value of the polynomial p(x) at x = a is 0, i.e., p(a) = 0.
Ex. : To find is x – 2 a factor of
p(x) = x3 – 3x2 + 4x – 4, we find the value of p(2).
p(2) = 23 – 3(22) + 4(2) – 4
= 8 – 3(4) + 8 – 4
= 8 – 12 + 8 – 4 = 0
=>x – 2 is a factor of x3 – 3x2 + 4x – 4.
Ex.1 Find the remainder when f(x) = 4x3 –3x2 + 2x – 4 is divided by x – 1.
Sol. When f(x) is divided by x – 1, then remainder = f(1).
Remainder = f(1) = 4(13) – 3(12) +
2(1) – 4
= 4 – 3 + 2 – 4 = –1
Ex.2 Find the value of a if x + a is a factor of the polynomial x3 + ax2 –2x + a + 15.
Sol. Here
0 = p(–a) = (–a)3 + a(–a)2 –2(–a) + a + 15
= –a3 + a3 + 3a + 15 = 3a + 15
=> 3a = –15 Þ a = –5
Ex.3 What must be added to 3x3 +x2 –22x +9 so that the result is exactly divisible by 3x2 + 7x –6.
Sol. Let p(x) = 3x3 + x2 –22x + 9 and
q(x) = 3x2 + 7x –6
We know if p(x) is divided by q(x) which is quadratic polynomial therefore if p(x) is not exactly divisible by q(x) then the remainder be r(x) and degree of r(x) is less than q(x) or Divisor.
By long division method
Let we added ax + b (linear polynomial) in p(x), so that p(x) + ax + b is exactly divisible by 3x2 + 7x –6
Hence, p(x) + ax + b = s(x) = 3x3 + x2 –22x + b = 3x3 + x2 – x(22–a) + (9 + b)
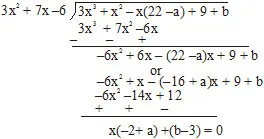
Hence, x (a –2) + b –3 = 0. x + 0
Þ a –2 = 0 and b – 3 = 0
Þ a = 2 or b = 3
Hence, if in p(x) we added ax + b or 2x + x then it is exactly divisible by 3x2 + 7x – 6.
Ex.4 Find the value of ‘a’ for which
x3 – 7x + 5 is a factor of
x5 – 2x4 – 4x3 + 19x2 – 31x + 12 + a.
Sol. By synthetic division remainder obtained on dividing
x5 – 2x4 – 4x3 + 19x2 – 31x + 12 + a by
x3 – 7x + 5 is a – 3.
If x3 – 7x + 5 is a factor of
x5 – 2x4 – 4x3 + 19x2 – 31x + 12 + a
=> Remainder a – 3 = 0
.. a = 3.
Ex.5 If ‘n’ is odd then prove that x +1 is a factor of xn + 1.
Sol. Let f(x) = xn + 1
Remainder f(– 1) = (– 1)n + 1
= – 1 + 1 = 0
(Since ‘n’ is odd (– 1)n = – 1
.. ‘x + 1’ is a factor of f(x).
Ex.6 When polynomial f(x) is divided by (x – 1), (x – 2) gives the remainders 5, 7 respectively. What is the remainder when same f(x) is divided by the (x – 1)(x – 2)?
Sol. If f(x) is divided by (x – 1) then remainder is f(1) = 5.
If f(x) is divided by (x – 2) the remainder is f(2) = 7.
If f(x) is divided by (x – 1) (x – 2) then remainder is of first degree
i.e., mx + n.
f(x) = (x – 1) (x – 2) q (x) + mx + n
f(1) = 5 Þ m + n = 5 ...(i)
f(2) = 2m + n = 7 ...(ii)
Solving (i) and (ii) we get m = 2, n = 3.
\ Remainder = 2x + 3
Ex.7 Find the factors of a (b – c)3 + b (c – a)3 + c (a – b)3.
Sol. To find the factors of
a (b – c)3 + b (c – a)3 + c (a – b)3 ...(1)
we see that the given expression vanishes when b = c.
Thus b – c is factor of the given expression (1)
Similarly (c – a), (a – b) are the factor of the expression (1).
Since the expression is of 4th degree, the remaining factor which should be
Symmetrical in a, b and c must be of the form k (a + b + c).
Thus a (b – c)3 + b (c – a)3 + c (a – b)3 = L (a + b + c) (a – b) (b – c) (c – a)
In order to find the value of ‘k’
Put a = 1, b = – 1, c = 2, we have
1 (– 3)2 – (– 1)3 + 2 (2)3
= k (1 – 1 + 2) (– 3) (1)
– 27 – 1 + 16 = k (– 12)
\ k = 1
Hence a (b – c)3 + b (c – a)3 + c (a – b)3 = (a – b) (b – c) (c – a) (a + b + c).
Ex.8 Find the factor of
a4 (b2 – c2) + b4 (c4 – a4) + c4 (a2 – b2).
Sol. Given that
a4 (b2 – c2) + b4 (c4 – a4) + c4 (a2 – b2)
By putting b2 = c2,
We find that the given expression vanishes, therefore (b2 – c2) is a factor of the expression.
Similarly (c2 – a2), (a2 – b2) are also the factor of the expression.
Now the product factors of (b2 – c2) (c2 –a2) (a2 – b2) is of 6th degree and the given expression is of 6th degree.
So the only factor if possible may be some constant factor.
Let some constant factor be k.
Putting a = 1, b = 2, c = 3, we have
(4 – 9) + 16 (9 – 1 + 81) (1 – 4)
= k (4 – 9) (9 – 1) (1 – 4)
– 5 + 128 – 243 = k (– 5) (8) (– 3)
– 120 = k . 120
k = – 1
Required factors are – (b2 – c2), (c2 – a2), (a2 – b2)
\ a4 (b2 – c2) + b4 (c2 – a2) + c4 (a2 – b2).
= – (b – c) (c – a) (a – b) (b + c) (c + a)
(a + b)
Ex.9 Find the factors of a (b – c)2 + b (c – a)2 + c (a – b)2 + 8 abc.
Sol. a (b – c)2 + b (c – a)2 + c (a – b)2 + 8 abc
...(i)
Now the expression vanishes on putting b = – c
Therefore (b + c) is a factor is (1).
Similarly (c + a), (a + b) are also the factors of (1).
The given expression is of third degree and the product of the factors so far obtained is also of third degree,
hence if any there may be a constant factor.
i.e.,
a (b2 – c2) + b (c2 – a2) + c (a2 – b2) + 2abc = k (b + c) (c + a) (a + b)
To evaluate k,
Putting a = 1, b = 1, c = 1, we have
1 (2) + (2) + 2 + 2 = k (2) (2) (2)
=> 8 = 8k Þ k = 1
a (b – c)2 + b (c – a)2 + c (a – b)2 + 8 abc
= (b + c) (c + a) (a + b)
Ex.10 Prove the identity
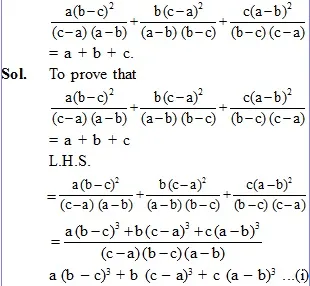
a (b – c)3 + b (c – a)3 + c (a – b)3 ...(i)
We see that the given expression (i) vanishes when b = c.
Thus b – c is factor of the given expression. Similarly (c – a), (a – b) are the factors of the expression.
Since the expression is of 4th degree; the remaining factor which should be symmetrical in a, b and c must be of the form L (a + b + c).
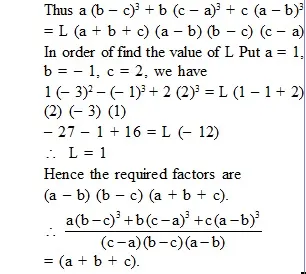
Ex.11 Factorise : –10x2 + 31x –24
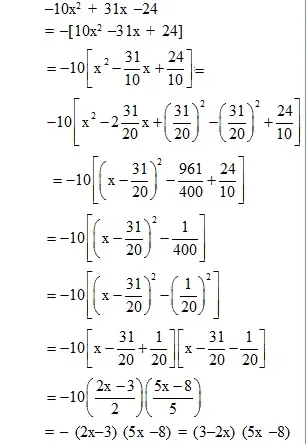
Ex.12 Suppose f(x) is polynomial of degree 5 and with leading coefficient 2001. Suppose further that f(1) = 1, f(2) = 3,
f(3) = 5, f(4) = 7, f(5) = 9. What is the valueof f(6).

.................................
h(5) = f(5) – 9 = 9 – 9 = 0
=> (x –1), (x–2), ..... (x –5) are factor of h(x)
=> h(x) = k(x–1) (x–2) (x–3) (x–4) (x –5)
f(x) = h(x) + (2x –1)
= k (x –1) (x –2) .......(x–5) + (2x–1)
To get ‘f’ as polynomial of degree ‘5’with leading coefficient 2001. Consider k = 2001
f(x) = 2001 (x – 1) (x – 2) (x – 3) (x – 4)
(x –5) + 2x –1